复杂网络上非马尔科夫易感-感染模型的二阶平均场求解

祁 婷,林诏华,冯 秘,唐 明

（1. 华东师范大学 通信与电子工程学院, 上海 200241; 2. 华东师范大学 物理与电子科学学院,上海 200241; 3. 香港浸会大学 物理系, 香港 999077）

0 引 言

疾病传播是当今复杂网络科学非常热门的研究课题之一, 传统的网络动力学模型是具有无记忆特性的马尔科夫过程, 即对于网络中所有的个体, 疾病传播过程和恢复过程都可以看成是典型的泊松过程[1-3]. 在马尔科夫过程中, 两个连续的感染过程或者恢复过程之间的时间间隔遵循指数分布, 换言之, 对当前的等待时间并不会影响未来的等待时间. 通过对传统的SIS(Susceptible-Infected-Susceptible)模型和SIR(Susceptible-Infected-Recovered)模型的平均场方法的研究, 可以发现马尔科夫假设极大地促进了复杂网络上动力学数学理论的发展[2-3].

然而, 越来越多的实证研究与经验分析表明, 现实生活中的人类活动往往呈现出具有“胖尾”时间分布的非马尔科夫特性[4-6]. 因此, 经典的马尔科夫框架仅仅是对真实世界的一个近似刻画.

网络中的非马尔科夫传播动力学近几年来引起了人们广泛的研究热情[7-15]. 马尔科夫理论无法精确地描述人与人之间的交互活动在很早以前就已经被注意到了, 同时也发现感染过程中的异质性会阻碍网络中疾病的扩散[8]. 消息传播理论求解了具有任意感染时间分布和恢复时间分布的SIR疾病传播模型[9]. 通过研究具有固定恢复时间分布以及“胖尾”感染时间分布的SIR模型, 发现了感染过程中的时序异质性能够显著抑制疾病的传播[10]. 一个比较重要的研究是, 通过重新定义有效感染率, 能够发现网络中传播动力学的马尔科夫过程与非马尔科夫过程在稳态时存在着等价性[11-13]. 两种经典的SIS模型的连边激活机制被提出后, 该等价性存在的条件被证明为激活边的产生与激活边指向的易感节点之间不存在时序相关性[13]. 另外, 在非马尔科夫传播动力学方面, SIR模型的点对近似理论以及SIS模型的淬火平均场理论最近也被提了出来[16-18].

求解网络传播动力学比较常用的方法是平均场理论. 早期的平均场方法假设了网络中的所有节点都能够在统计意义上等价[19]. 另外, 为了考虑网络度分布的异质特性, 异质平均场理论将网络中所有度相同的节点都视为等价[1]. 而淬火平均场方法则将网络中每个节点的连接情况都考虑到理论框架中[20-21]. 然而, 以上的理论方法都忽略了传播过程中节点与节点之间的动力学相关性, 为了克服这个困难, 点对近似理论深入地探究了两个邻接节点之间的相关特性[22-25]. 另外, 主方程理论能够得到更为精确的结果, 并且在一定条件下能够退化为平均场理论或者点对近似理论[26].

本文在前人工作的基础上, 提出了关于非马尔科夫 SI 模型的二阶平均场方法; 根据SI模型中易感态节点能转换为感染态节点而感染态节点无法转变为易感态节点的特点, 提出了闲置边的概念, 该方法能够求解SI模型的非马尔科夫爆发过程, 同时也能够预测每个节点被感染的平均时刻. 本文分别在真实网络和人工网络上进行了实验模拟, 并验证了以上研究成果的正确性和准确性.

1 非马尔科夫SI模型二阶平均场理论

1.1 非马尔科夫SI模型

在复杂网络的SI传播模型中, 节点存在着两种状态—易感态(S态)与感染态(I态), 其中I态节点有一定的概率将与其相连的S态节点感染成I态, I态节点却无法恢复为S态节点. 为了研究方便, 我们将无向网络中的无向边看作是两条方向相反的有向边, 对于有向边而言, 疾病的传播具有方向性, 只能是箭尾处的I态节点才能感染箭头处的S态节点. 在非马尔科夫SI模型中, 1条有向边存在着4种状态—〈SS〉态、〈SI〉态、〈IS〉态和〈II〉态, 分别表示该有向边的箭头节点为S态并且箭尾节点为S态、箭头节点为S态并且箭尾节点为I态、箭头节点为I态并且箭尾节点为S态、箭头节点为I态并且箭尾节点为I态.

如果1条有向边的箭头节点为易感态, 箭尾节点为感染态时, 即〈SI〉态, 这条边就被称为激活边,其他状态的边则被称为非激活边. 同时将当前时刻与该有向边成为激活边的时刻的时间差定义为激活边的状态年龄, 用K表示. 疾病的感染的传播满足特定的时间分布—感染时间分布ψinf(κ), 其物理意义在于, 1 条激活边传播疾病时的状态年龄K处在区间 [κ,κ+dκ)之内概率为ψinf(κ)dκ. 同时, 我们用ωinf(κ)表示激活边的感染率, 其物理意义为条激活边的状态年龄K如果处在区间 [κ,κ+dκ) 之内,则该激活边传播疾病将其指向的易感态节点感染的概率为ωinf(κ)dκ. 另外,ωinf(κ)dκ还可以理解为是, 激活边在状态年龄的区间 [0,κ)内没有传播疾病的前提下, 在状态年龄区间 [κ,κ+dκ) 传播疾病的概率. 则ψinf(κ) 与ωinf(κ) 的关系可以表示为

1.2 闲置边的定义

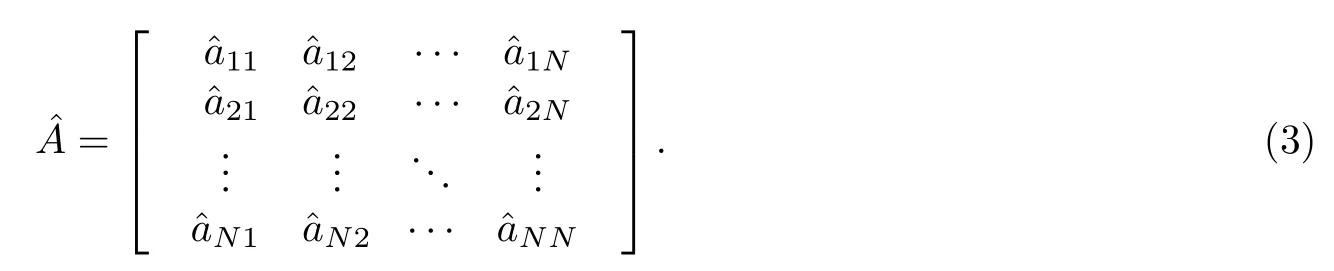
复杂网络可以由邻接矩阵A表示, 即

邻接矩阵A中的元素aij=1表示复杂网络中存在着有向边i←j(即由节点j指向节点i的有向边),aij=0 表示复杂网络中不存在有向边i←j. 值得注意的是, 在SI模型中, 某些有向边在整个爆发过程中始终不会成为激活边, 即始终不参与疾病的传播. 如图1所示, 红色节点为种子节点, 黄色节点为非种子节点, 蓝色边为无向边, 灰色和绿色的两条边是将无向边看作的两条有向边(所有无向边在理论计算时都应看作是两条方向相反的有向边, 但图中只画出了一条边被看作两条有向边). 对于疾病爆发而言, 疾病只能从节点j通过连边i←j传向节点i, 当节点i被感染后, 由于SI模型中的I态节点无法转变为S态节点, 故连边j←i将永远不可能变为激活边参与传播, 我们称这样的连边为闲置边, 见图1, 其中灰色的边即为闲置边.

图1 闲置边示意图Fig. 1 Schematic diagram of idle edges

但是在理论计算中, 这种闲置边也会参与计算, 而在实验模拟中这种边却不会参与疾病的传播,因此闲置边的存在会使计算误差增大, 故有必要将连边j←i对应的矩阵元素aji置为0. 我们将闲置边对应的矩阵元素值置为0后得到的矩阵记为, 即

为了得到, 我们需要判断邻接矩阵A中每个为1的元素所对应的边是否是闲置边, 然后将满足条件的元素置为0.

判定一条边j←i是否为闲置边的算法如下.

(1) 如果节点j为种子节点, 则j←i一定为闲置边, 反之, 则进行步骤(2);

(2) 将节点i标记, 如果存在节点k(kj)使得连边i←k存在, 则将节点k标记;

(3) 得到被标记的节点集合M, 如果存在节点l(l∈M)与节点k(k∈/M)使得连边l←k存在, 并且连边l←k不为连边i←j, 则将节点k标记;

(4) 不断重复步骤(3), 直到不再有新的节点被标记, 则进行步骤(5);

(5) 如果种子节点没有被标记, 则连边j←i是闲置边, 反之则不是.

通过以上算法我们可以判断网络中哪些边为闲置边, 进而可以得到矩阵.

而此方法的基本思想是, 如果某条边j←i为闲置边, 那么说明种子节点不可能通过连边j←i将节点j感染; 同样, 如果将疾病反向传播, 节点i在连边j←i不存在的条件下也无法将疾病传染给种子节点.

1.3 二阶平均场方法

对于节点而言, 我们定义Ii(t)和Si(t)分别为节点i在时刻t处于感染态和易感态的概率. 对于有向边, 我们定义 〈SS〉i←j(t) 、〈IS〉i←j(t) 、〈II〉i←j(t)分别为连边i←j在时刻t处于 〈SS〉态、〈IS〉态、〈II〉态的概率, 另外, 定义 〈SI〉i←j(κ;t)为连边i←j在时刻t处于〈SI〉态并且其状态年龄为κ的概率密度.

对于 〈SI〉 态的具有任意状态年龄的有向边, 只要它传播了疾病, 就能够将箭头节点感染为S态, 因此, 能够得到

被感染的S态节点会转化为I态节点, 因此可以得到关于Ii(t) 的表达式

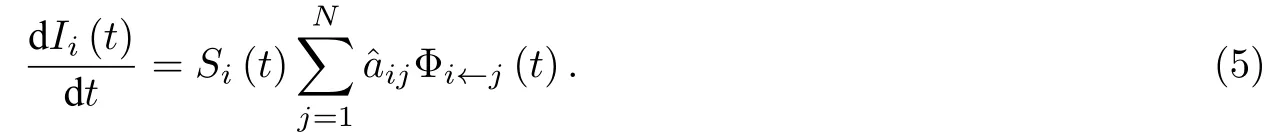
对于〈SS〉态连边而言, 其箭头节点被感染会转化为〈IS〉态连边, 其箭尾节点被感染会转化为〈SI〉态连边, 则 〈SS〉i←j(t) 的表达式可以表示为

其中, 式子右端第一项表示 〈SS〉态连边箭头节点被感染, 第二项表示箭尾节点被感染.

对于一个状态年龄为κ的〈SI〉态连边, 其箭头节点的感染方式有两种: 一种是箭头节点被除箭尾节点以外的其他节点感染; 另一种是箭头节点被箭尾节点感染. 如果其箭头节点在时刻t没有被感染,则在t+dt, 它的状态年龄将变为κ+dκ, 其中 dκ=dt. 因此可以得到

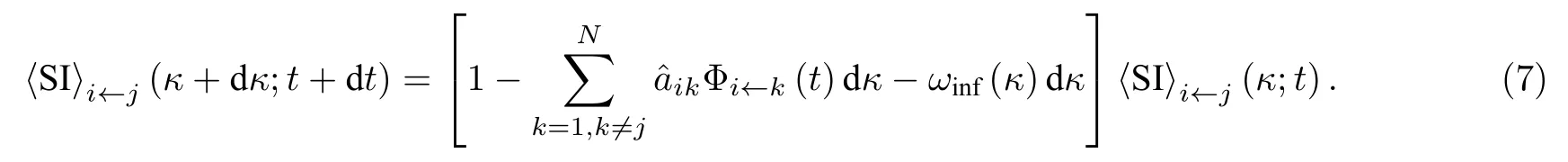
进而可以得到

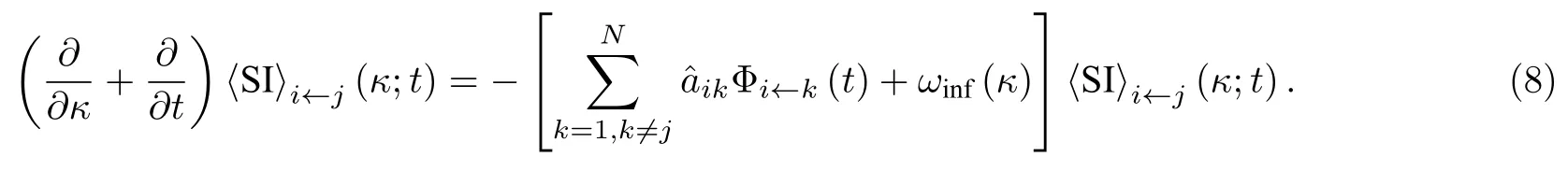
由于 〈SS〉态连边箭尾节点被感染会转变为状态年龄为0的 〈SI〉 态连边, 因此可以得到

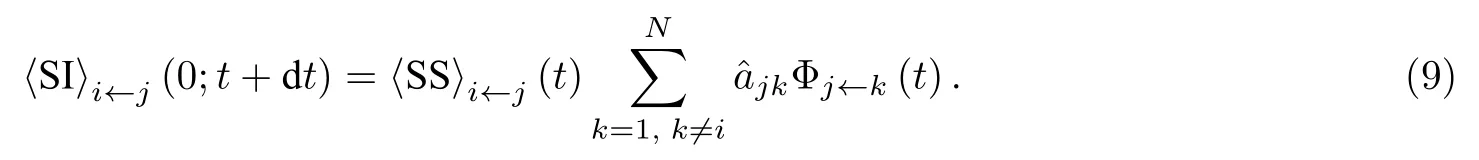
对于 〈IS〉态连边i←j而言, 其箭尾节点被感染会转化为 〈SI〉 态连边, 感染方式有两种: 一种是箭尾节点被除箭头节点以外的其他节点感染; 另一种是箭头节点通过连边j←i将箭尾节点感染, 则

其中, 等号右端的第一项表示 〈SS〉态连边转变为 〈IS〉态连边, 第二项和第三项表示 〈IS〉 态连边的箭尾节点被感染.

由于 〈SI〉态连边的箭尾节点被感染和 〈IS〉态连边的箭头节点被感染都会导致连边转化为 〈II〉 态,因此可以得到

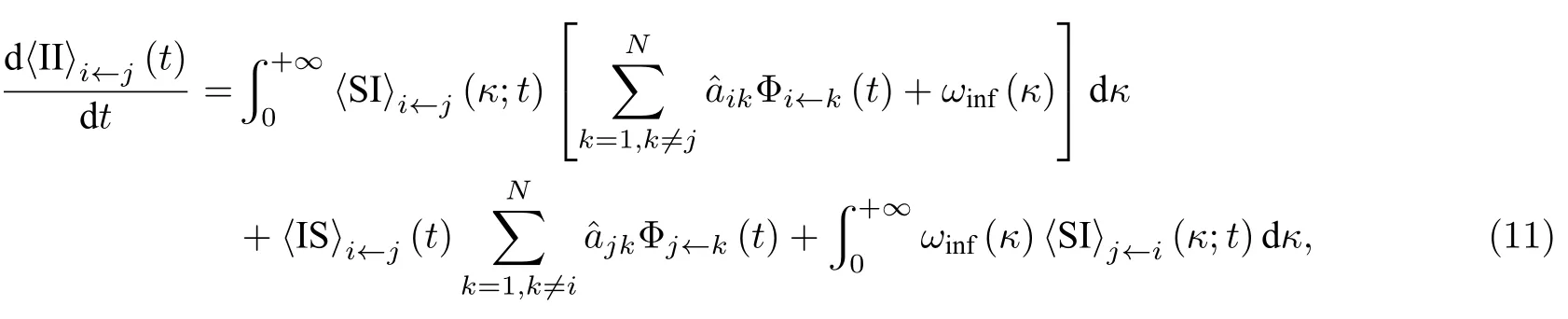
其中, 等号右端的第一项表示 〈SI〉态连边转变为 〈II〉态连边, 第二项表示 〈IS〉 态连边的箭尾节点被除箭头节点以外的其他节点感染, 第三项表示箭头节点通过连边j←i将箭尾节点感染.

1.4 平均感染时刻的预测

Ii(t)还有另外一层物理意义, 即节点i的被感染时刻小于t的概率. 根据概率论理论, 因为在 dt时间内Ii(t)的增量 dIi(t)即代表了节点i从S态变为I态的概率, 则可以表示为节点i的被感染时刻等于t的概率密度. 设节点i被感染的时间为Ti, 则其期望值E(Ti) 为

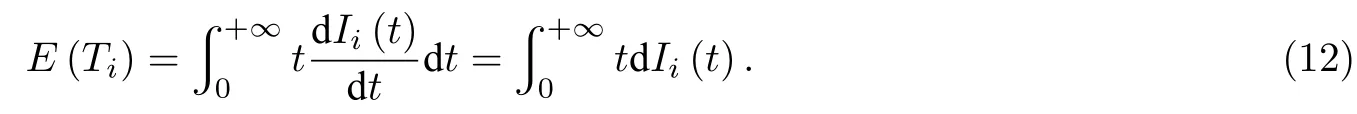
通过E(Ti)的计算, 就能够计算出节点i被感染的平均时刻, 进而就能够知道在复杂网络中, 对于拥有特定感染时间分布与特定种子节点的传播过程而言, 哪些节点能够迅速被感染, 哪些节点被感染则需要很长的时间.

值得注意的是, 公式(12)只适用于那些状态只能单向变换的模型, 如SI模型、SIR模型; 但对SIS模型而言, S态可以转变为I态, I态能够恢复为S态, 则公式(12)不再适用, 因为对于SIS模型,S态变为I态这个过程可以进行无穷次, 而对于SI模型和SIR模型在整个爆发过程中只会经历一次.

2 模拟验证

为了验证理论的正确性, 我们设置感染时间分布ψinf(κ) 为韦布尔分布, 即

设置βI=0.5,αI分别取 0.5, 1, 2, 4.αI和βI的下标I表示感染过程, 对于韦布尔分布,αI值越大,该分布的异质性越弱, 图象的分布越集中; 当αI=1 的时候, 该韦布尔分布为经典的指数分布. 对于4个值不同的αI, 其分布如图2所示, 随着αI值越来越大, 其图象的分布也越来越集中.

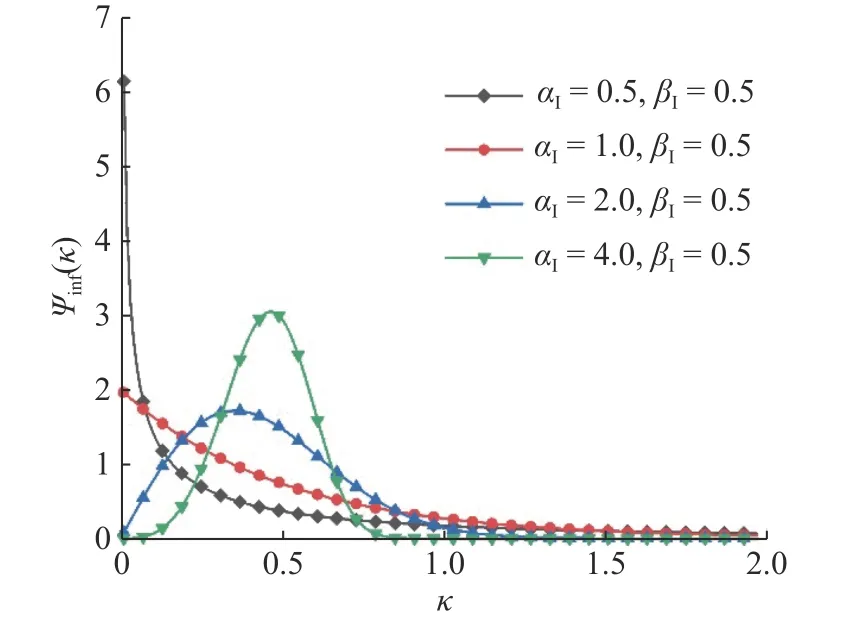
图2 韦布尔分布Fig. 2 Weibull distribution

同时我们分别测试了在BA(Barabási-Albert)无标度网络、ER(Erdős-Rényi)随机网络以及真实网络中SI疾病爆发的理论计算与实验模拟, 详见图3. 图3中, 横坐标t表示时间, 纵坐标I(t) 表示整个网络在时间t时的感染密度. 图3a) 为BA网络上的理论与模拟结果, 节点数N=10 000, 平均度 〈k〉=4 ;图3b) 为ER网络上的理论与模拟结果, 节点数N=10 000, 平均度 〈k〉=4 ; 图3c) 为真实网络上的结果. 为了后面能够在单个图象上全部展示所有节点被感染的平均时刻, 我们选取了1个节点数只有34的真实网络, 其平均度 〈k〉≈4.59. 该网络为著名的Zachary karate club网络, 且曾多次被相关领域的研究者所使用, 其数据是在1977年由 Zachary[27]所收集, 数据中的节点代表俱乐部里的成员, 无向连边表示相连的两个成员之间存在关系. 对于所有的实验模拟, 我们都是实验10 000次进行平均然后得到结果. 图3中的空心菱形、空心圆形、空心三角形、空心倒三角形的散点图分别代表αI取0.5, 1,2, 4的实验模拟结果; 实心菱形、实心圆形、实心三角形、实心倒三角形的图象分别代表αI取0.5, 1, 2,4的理论计算结果, 可根据公式(4)–公式(11)得到. 可以发现, 该理论在4个不同的参数下, 以及3个不同的网络中都可以很好地预测模拟结果, 其中随着αI值的减小, 网络爆发的速率逐步增大, 其主要的原因在于, 在爆发的初始阶段, 较小的αI值会导致更大的感染率, 使得在初始阶段其爆发速率增加,更多的被感染节点进而引发更快的传播速率.

图3 SI模型理论与模拟对比图Fig. 3 Comparison between the theory and simulation of the SI model

另外, 我们也测试了在真实网络中每个节点被感染时间的平均值, 并与理论计算值进行了比较,结果见图4. 图4a)、图4b)、图4c)与图4d)分别代表了αI为0.5, 1, 2, 4时的理论与模拟的图象, 其中横坐标代表节点i的编号, 纵坐标代表节点被感染的平均时间E(Ti), 方形代表理论计算的图象, 三角形代表实验模拟的图象, 理论结果是根据公式(4)–公式(12)得到. 可以发现, 我们的理论能够很好地预测每个节点被感染时刻的平均值. 我们发现, 随着αI的增大, 节点被感染的平均时刻在整体上逐渐增大, 并且部分节点在αI比较小的时候, 被感染的平均时刻参差不齐, 却随着感染时间分布的异质性的减小, 这些节点被感染的平均时刻趋于相同. 如编号为2到9的节点, 在αI=0.5 时, 这些节点被感染的平均时刻各不相同, 但是当αI=4.0, 其对应的数值基本相同. 节点被感染的平均时刻E(Ti) 的引入, 也让我们更加清楚地认识到在SI模型的疾病爆发过程中, 不同异质性的感染时间分布下, 疾病从种子节点到特定目标节点的时间是呈现各种各样的非线性性. 在现实生活中, 如果我们掌握了疾病或者消息的传播网络结构, 以及对应的感染时间分布, 我们就能够确定出哪些节点更容易被快速感染.

图4 真实网络中不同参数下各个节点被感染平均时刻Fig. 4 Average time for a single node to be infected in real networks with different parameters

3 主要结论

本文首先给出了闲置边的概念, 然后通过闲置边概念的引入提出了一种能够求解非马尔科夫SI模型的二阶平均场方法, 该方法能够很好地预测复杂网络上非马尔科夫SI模型的爆发过程, 并且发现随着感染时间分布异质性的变强, 爆发的速率也会随之增加. 通过求解SI模型的时间演化过程,该理论还能够得到每个节点被疾病感染的平均时刻, 并且理论计算值也能够非常准确地预测实验模拟结果, 即我们能够利用该理论对于特定的感染时间分布, 在特定的网络上, 预测哪些节点能够更快地被感染, 哪些节点被感染需要花费更多的时间, 为控制疾病或谣言在网络中的传播提供理论支撑.