利用超高斯光模拟方势垒

李佳欣,董光炯

（华东师范大学 精密光谱科学与技术国家重点实验室, 上海 200241）

0 引 言

量子隧穿效应是指即使粒子动能低于势垒高度仍能以一定概率穿过势垒的现象, 这是粒子波动性的直接体现. 1927年, Hund[1]首次注意到隧穿现象的几率问题; 同年, Nordheim[2]应用薛定谔方程计算了电子从多种不同表面反射的反射系数. 随后隧穿效应被广泛应用于原子分子物理、核物理和固体物理的研究. 例如, Oppenheimer[3]根据隧穿计算了外场作用下氢原子的电离率; Gamow, Gurney和Condon用隧穿来解释α粒子衰变[4-6]; Millikan等[7-8]用隧穿来解释金属表面的场致发射; Bardeen等[9]用隧穿来研究电子输运现象. 在这些理论研究基础之上, 基于量子隧穿效应的各种器件应运而生,如1957年Esaki根据半导体中的带间隧穿现象发明了隧穿二极管[10], 1982年Binnig等[11-12]研制了扫描隧道显微镜.

方势垒和双方势垒的散射问题[13]是量子隧穿的理论研究中重要的解析可解模型. 方势垒散射的解析解不仅给出了粒子反射、透射率, 而且是进一步研究量子力学中的时间问题(比如隧穿时间问题)的基础[14-20]. 在对双方势垒的研究中, Tsu 等[21]、Chang等[22]发现了共振隧穿的现象. 在实验上实现有质粒子(如电子、原子)的方势垒, 对于研究量子隧穿问题具有重要的意义.

激光操控是原子分子气体操控的重要实验手段. 近年来激光光束整形技术[23-25]快速发展, 进一步丰富了原子分子光力操控技术[26-28], 其中的一个重要的进展是能制备高质量的超高斯光束[29-35]. 超高斯光又称平顶光, 它的光强在中心近似均匀, 而在离开光斑区域则迅速下降为零. 超高斯光的光强空间分布的平顶特征为实现量子力学中方势垒、方势阱等提供了可能. 文献[36]首先提出利用超高斯光和冷分子相互作用的方势阱实现分子镜, 为物质波操控以及量子力学理想模型的实验研究提供了一条新途径. 随后, 在超冷原子隧穿问题的研究中, 超高斯光和原子相互作用的电偶极势能被视为实现方势垒的重要手段[37-38]. 然而, 在这些超冷原子研究中并没有真正研究超高斯光对超冷原子的散射问题,尤其是没有处理不同阶数的超高斯光对隧穿的影响.

本文中研究利用了超高斯光实现方势垒的理论途径, 一是利用具有大蓝失谐超高斯光和原子相互作用势能实现, 二是利用电子在超高斯光场中受到的有质动力势能[39-40]实现. 此外, 还进一步研究了超高斯势垒的空间形状对隧穿的影响, 发现超高斯光的阶数需要大于20才能很好模拟方势垒的散射. 最后, 研究了双超高斯势垒模型中的共振隧穿. 本文工作对于用超高斯光模拟量子力学基本模型的实验研究具有参考价值.

1 一维超高斯势垒散射的理论模型

以光束传播的方向为z方向, 一束超高斯光在焦平面的光强分布可以描述为[30-32]

其中,wx和wy分别是超高斯光束在x、y方向的e−1光斑半径,m、n分别是超高斯光的阶数. 当超高斯光的阶数远远大于1时, 超高斯光的光束在和的区域, 光强近似等于I0, 而一旦离开此区域光强则以超指数形式减小. 因此, 超高斯光束又称为平顶光束. 目前实验上, 超高斯的阶数可以达到200[30]. 这些技术进步使得超高斯光的平顶特征非常适合于构造量子力学中的理想模型, 如方势阱和方势垒.

本文现在研究用超高斯光构造一个方势垒的可能途径.

1.1 利用远离共振的蓝失谐光和原子相互作用形成的势能模拟方势垒

首先研究超高斯光和超冷原子的相互作用. 考虑超高斯光的频率远大于电子跃迁频率(远离电子共振跃迁的蓝失谐), 则可以忽略光和原子相互作用的自发辐射. 在这种情况下, 光和原子相互作用是电偶极势能为主, 其电偶极势能为[41]

其中,U0=αI0,α是原子极化率.

考虑超冷原子束从x轴方向入射. 如图1所示, 假设wy远远大于原子束的宽度, 则

图1 超高斯势垒示意图Fig. 1 Diagram of a super-Gaussian barrier

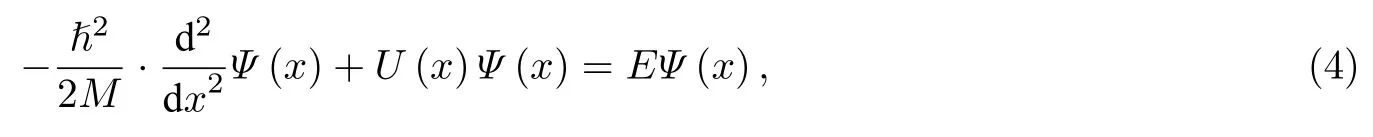
式中,M为入射原子的质量,E为入射原子的能量. 当超高斯光的阶数足够大, 势垒(2)可以近似为方势垒, 如图2所示.

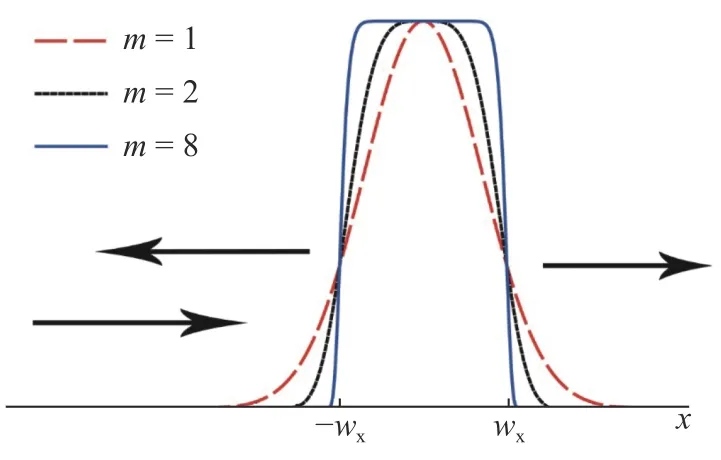
图2 一维超高斯势垒散射模型示意图Fig. 2 Schematic diagram of a one-dimensional super-Gaussian barrier scattering model

1.2 超高斯光和电子束的有质动力学势模拟方势垒

考虑电子束从x轴正方向入射, 假设电子束宽度足够宽, 可以近似为平面波, 同时电子束y方向的宽度又远远小于wy, 则超高斯光和电子束相互作用的有质动力学势能为[42]

其中,e是单位电子电荷,ε0是真空介电常数,Me是电子质量,ω是光频率,c是真空中光速. 由于光频率巨大, 在公式(5)等号右端根号中第二项通常远小于1, 因此式(5)可化为

其中,

可见超高斯光和电子束的有质动力学势能在超高斯光阶数足够时可以模拟方势垒, 电子被超高斯光散射后的系统同样可以被方程(4)所描述.

2 超高斯势垒形状对方势垒模拟的影响研究

图2显示超高斯光的阶数m越大, 势垒的形状越接近一个宽度为 2wx, 高为U0的方势垒US, 其形式为

其中,wS=2wx是势垒宽度. 对于宽度为wS、势垒高度为U0的一维方势垒模型, 能量为E的粒子的透射系数的解析形式为[43]

对于超高斯势垒的散射问题, 我们求解方程 (4). 这个方程不能解析求解, 我们利用数值求解. 在远离超高斯势垒的左侧, 既有入射波也有反射波, 波函数的形式可写为

在远离超高斯势垒的右侧, 只有透射波, 波函数的形式可写为

式中,Ae−ikx和Beikx分别表示反射波和透射波. 利用边界处波函数及一阶导数连续条件采用有限差分法[44]可数值求解方程 (4)的系数A,B以及波函数Ψ(x), 则透射系数为

表示粒子透过势垒的几率.

下面比较不同阶数的超高斯势垒与方势垒的透射系数. 在数值计算中, 取wx=3λ0,U0分别为0.01ER和 0.1ER, 其中λ0为光波长,为反冲动能,h为普朗克常数. 改变入射动能E和阶数m, 得到不同的透射系数如图3a)和3c)所示. 当U0=0.01ER时, 在入射动能小于1/5势能处透射率基本为0; 在入射动能大于1/5势能处, 透射系数逐渐增大; 当入射动能等于势能时, 透射率可达0.25, 这与经典粒子穿越势垒有很大区别. 当U0=0.1ER时, 在入射动能小于4/5势能处透射率基本为0; 在入射动能大于4/5U0势能处, 透射系数逐渐增大; 当入射动能等于势能时, 透射率最高仅达到0.07, 可见势垒高度的增加使透射率大大降低. 从图中可以看到, 高阶的超高斯势垒和方势垒的透射系数十分相近, 为了更好地观察, 我们研究了两者透射系数相对差δT=|TSG−TS|随入射动能变化的趋势(这里为了区别不同的势垒对应的透射率, 我们对透射系数加下标：下标 S 对应方势垒; 下标SG对应超高斯势垒). 如图3b)和3d)所示, 超高斯势垒的阶数越高, 其透射系数越接近方势垒透射系数,即这个超高斯势垒的性质更接近方势垒.

图3 透射系数随入射能量的变化Fig. 3 Transmission coefficient as a function of incident energy

接下来进一步探究阶数与模拟效果之间的关系. 给定一个m阶超高斯势垒, 我们在入射能量介于0到U0之间均匀取N个入射能量E1,E2,···,EN−1,EN, 然后计算相应的透射率(k=1,2,···,N). 对于方势垒在入射能量Ek的透射率记为TS,k. 我们定义m阶超高斯势垒的模拟方势垒的平均偏差为

如图4所示, 随着阶数m的增大,迅速衰减, 由此可见, 在m<100 时增大阶数可使模拟质量得到快速提升. 当m=20 时,已经接近10–3, 此时超高斯势垒可以较好地模拟方势垒.

图4 (随阶数 m 的变化Fig. 4as a function of the order m

3 双超高斯势垒中共振隧穿现象的研究

粒子入射到有多个势垒的势场时会在势垒间发生多次反射. 当入射能量和势垒间的某个模式发生共振, 透射率会等于1, 这个现象就是量子隧穿中重要的共振隧穿现象. 因此我们进一步研究了双超高斯势垒的共振隧穿现象. 这个双超高斯势垒的表达式为

其示意图如图5所示, 其中d是两个势垒中心之间的距离. 在数值计算中, 我们取U0=0.01ER,wx=3λ0,d分别取 10λ0和 15λ0, 研究了不同间距的双超高斯势垒透射率随入射动能的变化. 透射率随入射能量变化的数值计算结果如图6所示, 图6a)和图6b)分别对应势垒间距等于 10λ0和 15λ0的情况. 图6显示出共振隧穿现象. 共振峰的个数可以通过调整势垒间距来控制. 共振峰的细节在图中通过小图显示. 对于不同阶数的超高斯光, 共振位置不一样. 随着阶数的增加, 共振峰对应的入射能量也增加.

图5 双超高斯势垒散射模型示意图Fig. 5 Schematic model for double super-Gaussian barrier scattering

图6 透射率随入射能量的变化Fig. 6 Transmittance as a function of incident energy

4 结 论

本文从理论上研究了用超高斯光束模拟方势垒的问题. 首先分别利用具有大蓝失谐超高斯光和原子相互作用势能以及超高斯光和电子的有质动力势能实现超高斯形势垒, 再进一步研究了超高斯势垒的空间形状对隧穿的影响, 发现超高斯光的阶数在大于20时即可较好模拟方势垒. 随着超高斯光场阶数m的增大, 提高阶数仍能提升模拟质量, 但变化幅度较小, 性价比不高. 最后, 研究了入射粒子入射到双超高斯势垒的共振隧穿现象, 本文的数值计算表明, 通过调整势垒之间的距离可以控制共振峰的位置以及个数. 本文的研究结果对使用超高斯光模拟量子力学中方势垒模型的实验研究具有参考价值, 可以用于研究量子力学的基本问题, 比如隧穿时间问题[14-20]. 目前对于隧穿时间的实验研究[18-20],都用零质量的光子, 它受到材料吸收的影响[45-46]. 而采用原子或者电子作为入射粒子, 可以研究有质量粒子的隧穿时间问题. 在目前的研究中, 本文只考虑了单粒子的隧穿问题, 进一步的研究可以考虑多粒子体系, 研究入射粒子的量子统计性质对隧穿的影响, 比如对于费米子, 入射粒子数目的奇偶性有关的隧穿现象值得进一步研究[47].