多重线性多项式在3 × 3阶上三角矩阵代数上的像

孙爱慧,白 杰, 包开花

（1. 吉林师范大学 数学学院, 吉林 四平 136000; 2. 上海师范大学 数学系, 上海 200234;3. 内蒙古民族大学 数理学院, 内蒙古 通辽 028000）

0 引 言

著名的Lvov-Kaplansky猜想断言: 一个域K上的多重线性多项式关于矩阵代数Mn(K) 上的像总是一个向量空间[1]. 文献[2-4]中讨论了 4 次多重线性多项式的情形. 2012年, Kanel-Belov、Malev和Rowen[1]解决了n=2 时的Lvov-Kaplansky猜想. 2016年, Kanel-Belov、Malev和Rowen[5]解决了n=3时的Lvov-Kaplansky猜想. 文献[6-9]进一步讨论了Lvov-Kaplansky猜想.

2019年, Fagundes[10]考虑了Lvov-kaplansky猜想的一个变形, 得到了严格上三角矩阵代数上多重线性多项式的像的完整描述. 同年, Fagundes和Mello[11]提出了Lvov-Kaplansky猜想的另一种变化形式.

猜想 0.1域K上的多重线性多项式关于上三角矩阵代数Tn(K) 上的像总是一个向量空间.

Fagundes和Mello[11]讨论了次数小于4的多重线性多项式情形的猜想0.1. 2019年, Wang等[12-13]给出了n=2 时猜想0.1的肯定回答.

设K是一个域,K∗=K{0},n≥2(n∈N).K上的全体n阶上三角矩阵集记作Tn.K上的全体n阶严格上三角矩阵集记作Tn(K)(0). 更一般地, 若k≥0, 对于满足j−i≤k时的 (i,j) 项为零的所有上三角矩阵的集合记作. 本文的目的是给出n=3 时猜想0.1的一个肯定回答. 下面给出本文的主要结果.

定理 0.1设m≥1,K是一个满足|K|>3 的域. 设f(x1,···,xm) 是一个K上的多重线性多项式,则f(T3) 必为或.

本定理的证明方法主要借鉴了文献[12]中的方法.

1 主要结果的证明

设f(x1,···,xm) 是域K上的关于非交换变量的多重线性多项式

其中λσ∈K,Sm是一个m元对称群.

取定k∈{1,···,m}, 对于每一个s∈{1,···,m},T⊆{1,···,k−1,k+1,···,m}, 且|T|=s−1(若s=1, 则T=∅ ), 定义

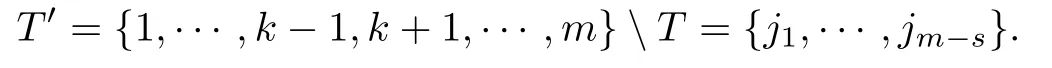
取定k1∈T′. 对于任意的s1∈{s+1,···,m},T1⊆T′{k1}, 且|T1|=s1−s−1 (若s1=s+1, 假定T1=∅), 定义

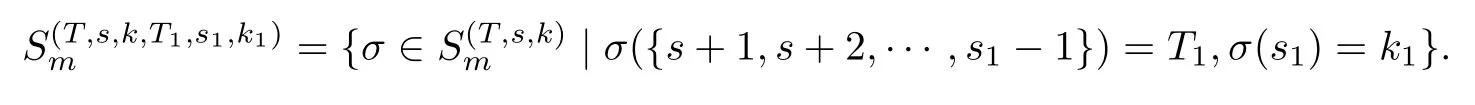
设

容易看出,g的所有系数和等于βT,s,k.

用eij表示 (i,j) 分量为 1、其余分量都为 0 的矩阵. 令

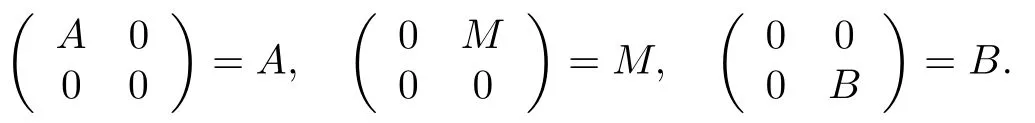
显然Tn=A+M+B.又有AM,MB⊆M;AB=BA=M2=MA=BM={0}.

先给出如下简单引理.

引理 1.1设K是一个域,m≥1 和n≥2均为整数,f(x1,···,xm)是K上的非零多重线性多项式.若α0, 则f(Tn)=Tn; 若α=0, 则f(A)={0}.

证 明当α0 时, 对于任意的u∈Tn, 有

由α0, 根据上式可得, 对于任意的u∈Tn, 均有

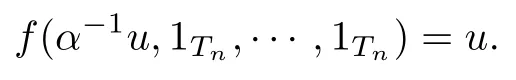
这意味着f(Tn)=Tn.

当α=0 时, 对于任意的a1,···,am∈A, 有

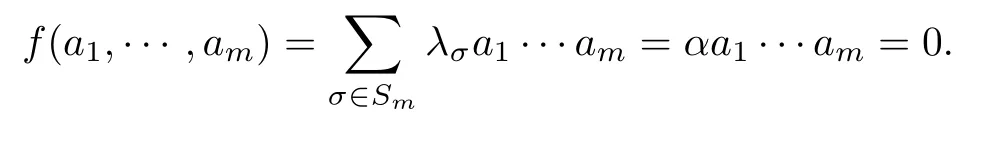
因此,f(A)={0}.

下面的结果见文献[13]中的引理3.

引理 1.2[13]设K是一个域,f(x1,···,xm)是K上的一个多重线性多项式, 那么

(i) 若α0, 则f(T2)=T2;

(ii) 若α=0, 且对于任意的T,s,k, 有βT,s,k=0, 则f(T2)={0};

(iii) 若α=0, 且存在T,s,k, 使得, 则.

以下结果对于证明本文的主要结果是至关重要的.

引理 1.3设K是一个域, 满足|K|>3m≥2,是一个整数,f(x1,···,xm)是K上的一个多重线性多项式. 假定α=0, 且存在T,s,k, 使得βT,s,k0, 则.

证 明由引理1.1, 有f(A)={0}. 由f(A∪M)⊆M以及引理1.2(iii), 有

可得f(B∪M)⊆M+B(0). 所以,f(A∪M∪B)⊆M+B(0). 由于f是多重线性的, 可得f(T3)⊆M+B(0). 又

对于每个i∈{1,···,k−1,k+1,···,m}, 若i∈T, 则设ci=e11; 若i∈T′, 则设ci=e22+e33. 由式(1), 那么对于任意的λ,µ∈K, 有

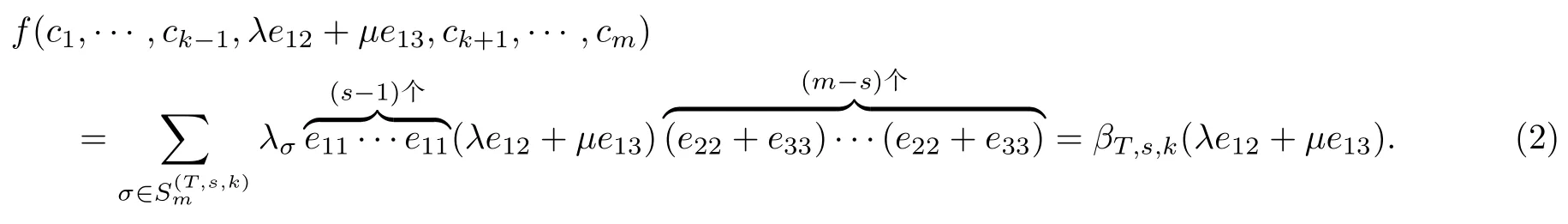
若i∈T, 则设di=e22; 若i∈T′, 则设di=e33. 那么对于任意的ν∈K, 有

对于t∈{1,···,m−s}, 存在λj1,···,λjt,wt∈K∗, 使得对于任意的i=1,···,t, 有

对于任意的i=t+1,···,m−s, 设dji=e33; 对于任意的i∈T, 设di=e22; 对于任意的ν∈K, 有

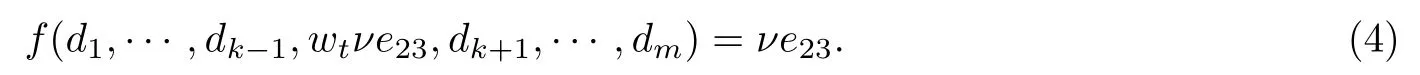
接下来, 对t用归纳法来证明该推断. 假设t=1, 令

其中λj1∈K. 若j∈T′, 且满足jj1, 则设dj=e33; 若i∈T, 则设di=e22. 由式(3)可得, 对于任意的λj1,ν∈K, 存在ρ1,ρ2∈K, 使得

首先假定ρ10. 由|K|>3 可知, 存在λj10, 使得

由式(5), 对于任意的ν∈K, 有

下面假定ρ1=0. 由式(5), 对于任意的λj1,ν∈K, 有

特别地, 由式(3)和式(7), 对于任意的ν∈K, 分别取λj1=1 和λj1=0, 有

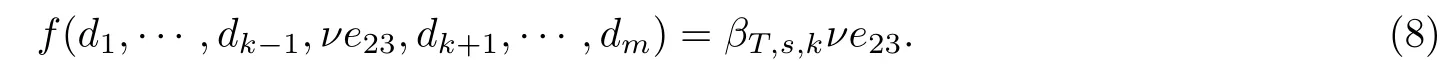
若ρ10, 设w1=(βT,s,k+λj1ρ1+ρ2)−1; 若ρ1=0, 设. 由式(6)和式(8), 对于任意的ν∈K, 有

现在考虑t≥2的情形. 通过归纳可得, 存在λj1,···,λjt−1∈K∗,wt−1∈K∗, 使得对于l=1,···,t−1, 有

对于任意的j=jt,···,jm−s, 取dj=e33; 对于任意的i∈T, 取di=e22. 则对于任意的ν∈K, 有

设

其中λjt∈K. 由式(10), 对于任意的λjt,ν∈K, 存在ρ3,ρ4∈K, 使得

首先假定ρ30. 由|K|>3可知, 存在λjt0, 使得

由式(10), 对于任意的ν∈K, 有

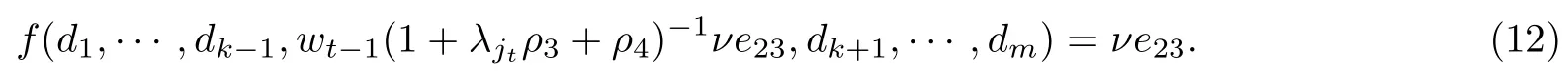
下面假定ρ3=0. 由式(11), 对于任意的ν,λjt∈K, 有

特别地, 由式(10)和式(13), 对于任意的ν∈K, 分别取λjt=1,λjt=0, 有

若ρ30, 则设wt=wt−1(1+λjtρ3+ρ4)−1; 若ρ3=0, 则设wt=wt−1,λjt=1. 由式(12)与式(14),对于任意的ν∈K, 有

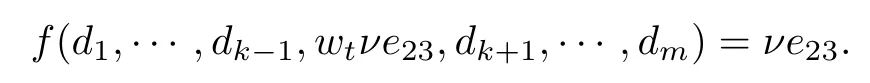
于是, 证明了前面的推断. 设t=m−s,w=wm−s, 由式(4)可知, 存在λj1,···,λjm−s,w∈K∗, 使得

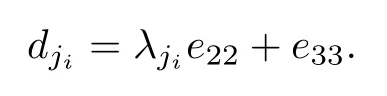
对于任意的i∈T, 有di=e22. 对于任意的ν∈K, 有

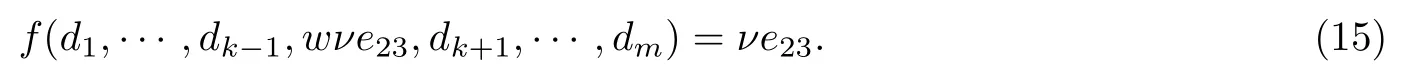
对于任意的t=1,···,m−s, 设cjt=λjte22+e33. 若i∈T, 设ci=e11. 由式(2), 对于任意的λ,µ∈K, 有

并且在式(15)与式(16)中, 对于任意的j∈T′, 有cj=dj.

对于t∈{1,···,s−1}, 可断言, 存在λi1,···,λit,pt,qt∈K∗, 使得cil=e11+λile22. 其中, 对于任意的l=1,···,t, 有il∈T; 对于任意的l=t+1,···,s−1, 有cil=e11; 对于任意的l=1,···,m−s,有cjl=λjle22+e33,jl∈T′; 对于任意的λ,µ∈K, 有

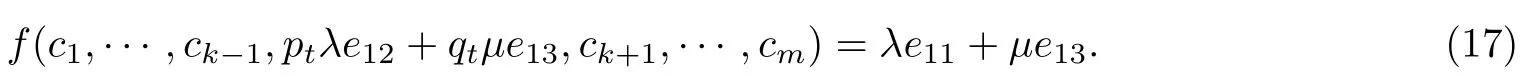
假定t=1. 对于i1∈T, 设ci1=e11+λi1e22, 其中λi1∈K; 对于任意的i∈T{i1}, 有ci=e11.设cjl=λjle22+e33, 其中对于任意的l=1,···,m−s, 有jl∈T′. 由式(16), 对于任意的λ,µ,λi1∈K, 有

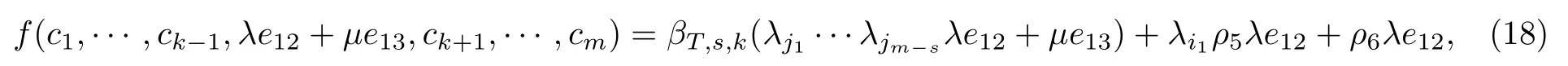
其中ρ5,ρ6∈K. 首先假定ρ50. 由|K|>3可得, 存在λi10, 使得

接下来假定ρ5=0. 由式(18), 对于任意的λi1,λ,µ∈K, 有

由式(16)与式(20), 对于任意的λ,µ∈K, 分别取λjt=1,λjt=0, 有

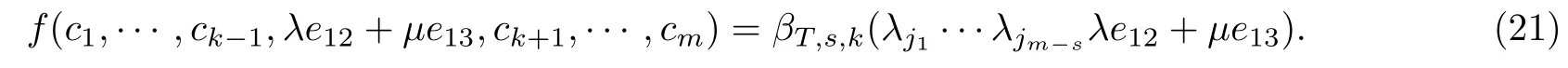
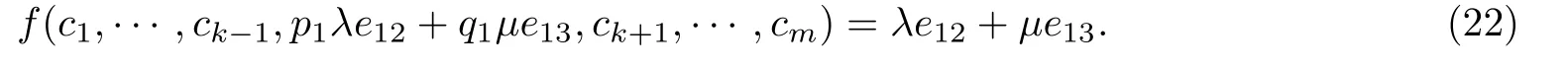
这证明了t=1的情形. 当t≥2时, 由归纳法可知, 存在λil,pt−1,qt−1∈K∗, 使得对于任意的l=1,···,t−1, 有cil=e11+λile22; 对于任意的l=t,···,s−1, 有cil=e11. 对于任意的l=1,···,m−s, 有cjl=λjle22+e33. 对于任意的λ,µ∈K, 有

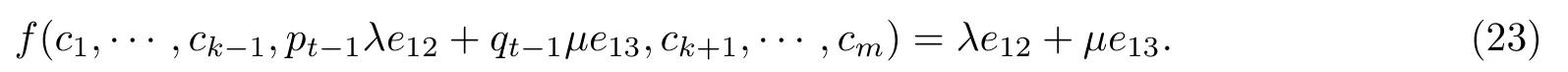
设

其中λit∈K. 由式(23), 对于任意的λ,µ,λit∈K, 有

其中ρ7,ρ8∈K.

首先假定ρ70. 由|K|>3可得, 存在λit0, 使得

由式(24), 对于任意的λ,µ∈K, 可得

下面假定ρ7=0. 由式(24), 对于任意的λ,µ,λit∈K, 可得

由式(23)和式(26)可得, 对于任意的λ,µ∈K, 分别取λjt=1 或λjt=0, 有

若ρ70, 设pt=pt−1(1+λitρ7+ρ8)−1,qt=qt−1; 若ρ7=0, 设pt=pt−1,qt=qt−1,λit=1. 由式(25)和式(27)可得, 对于任意的λ,µ∈K, 有

于是证明了前面的推断. 假定t=s−1,p=ps−1,q=qs−1, 由式(17)可得, 存在λi1,···,λis−1,p,q∈K∗, 使得

其中对于任意的l=1,···,s−1, 有il∈T;

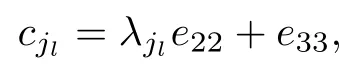
其中对于任意的l=1,···,m−s, 有jl∈T′. 对于任意的λ,µ∈K, 有

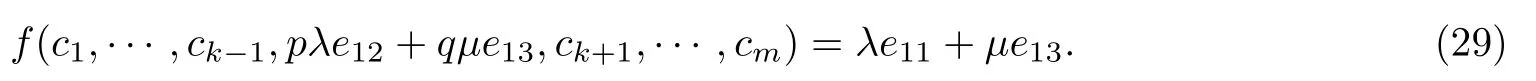
对于任意的t=1,···,s−1, 设dit=e11+λite22. 由式(15), 对于任意的ν∈K, 有

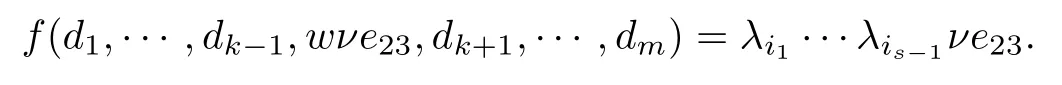
于是, 对于任意的ν∈K, 有

并且, 在式(29)与式(30)中, 对于任意的i∈{1,···,k−1,k+1,···,m}, 有ci=di. 由式(29)与式(30), 对于任意的λ,µ,ν∈K, 有

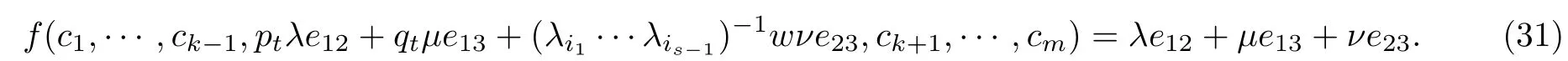
引理证毕.

下面证明本文的主要结果.

定理 0.1的证明若m=1, 结论显然成立. 不妨假定m≥2. 首先假设α0. 由引理1.1可得f(T3)=T3.

下面假定α=0. 则由引理1.1可得f(A)={0}. 对于T,s,k, 若βT,s,k0, 由引理1.2(iii)可得f(T3)=T3(0). 对于任意的T,s,k, 假定βT,s,k=0. 由引理1.2(ii)可得f(B)={0}. 所以有f(A∪B)={0}.对于任意的ci∈A(i∈T)与ci∈B(i∈T′), 设

由式(1), 对于任意的u∈M, 有

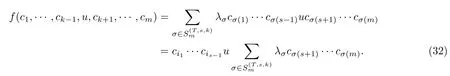
若s=m, 由式(32)可得, 对于任意的u∈M, 有

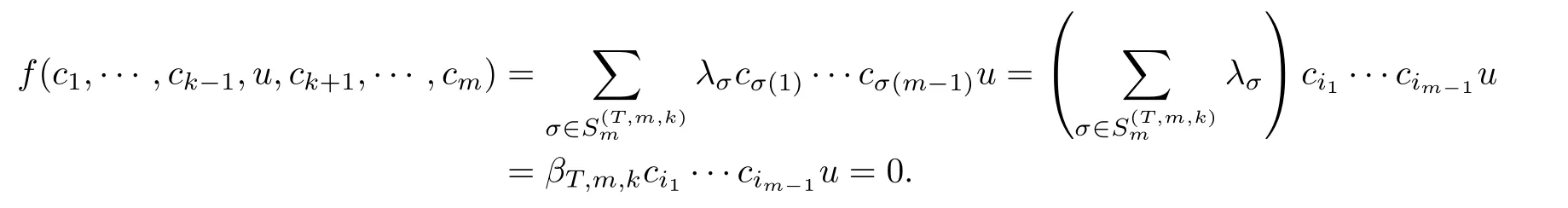
这表明f(A∪M)={0}. 设

由βT,s,t=0可得,g的所有系数之和为零. 接下来分两种情况证明.

情形 1对于任意的T,s,k,T1,s1,k1, 有βT,s,k,T1,s1,k1=0. 由引理1.2(ii)可得g(B)={0}. 由式(32), 对于任意的u∈M,

又因为f(A∪B)={0}, 所以由式(33)得

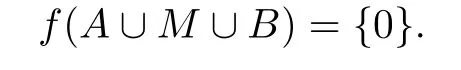
由f是多重线性的, 可得f(T3)={0}.

情形 2存在T,s,k,T1,s1,k1, 使得βT,s,k,T1,s1,k10. 对于g应用引理1.2(iii)可得

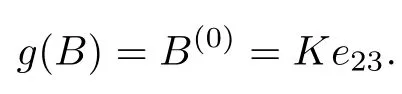
由于f(A∪B)=f(A∪M)={0}, 由式(32)可得

由于f是多重线性的, 可得. 由g(B)=B(0)可得, 存在cj∈B, 对于任意的j∈T′, 有

对于任意的i∈T, 设ci=e11. 由式(32), 对于任意的λ∈K, 可得