一类差分多项式的零点和唯一性
王乙萍,黄志刚
(苏州科技大学 数理学院, 江苏 苏州 215000)
0 引 言
本文假定读者熟悉Nevanlinna值分布理论的一些基本概念和标准记号[1-4]. 设f(z) 是复平面上的亚纯函数, 用T(r,f)表示复平面上亚纯函数f(z)的特征函数,λ(f)表示复平面上亚纯函数f(z) 的零点收敛指数,σ(f)表示复平面上亚纯函数f(z)的增长级. 如果亚纯函数α(z)满足T(r,α(z))=S(r,f), 则称α(z)为关于f(z)的小函数, 其中S(r,f)表示任意满足S(r,f)=o(T(r,f)),r→∞, 的量, 最多有可能除去一个r的有限对数测度例外集. 假设f(z) 和g(z)为非常数亚纯函数,a为任意复数. 如果f(z)−a和g(z)−a有相同的零点, 且重数也相同, 则称a为f(z) 和g(z)的 CM 分担值; 若不计零点的重数, 则称a为f(z) 和g(z)的 IM分担值. 另外, 设p是正整数, 用表示关于f−a的零点的计数函数, 假设z0是f−a的m重零点. 若m≤p, 则f−a的零点记为m重; 若m>p, 则f−a的零点记为p重.
定义 1[5]令是非零多项式, 其中是复常数,Γ0=m1+2m2, 这里的m1表示P(z)的单重零点的个数,m2表示P(z) 的多重零点的个数. 记d=gcd(λ0,λ1,···,λn), 其中
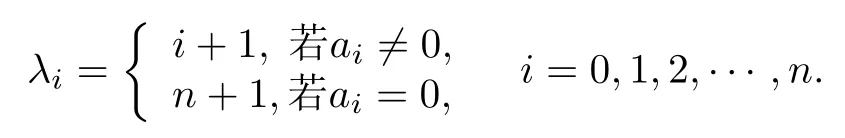
1959年, Hayman[6]在f(z) 是有限级亚纯函数的条件下, 得出了两种特殊形式的微分多项式和的值分布. 之后, 许多学者研究了一般形式的微分多项式的值分布, 并取得了一些重要成果. 近年来, Halburd-Korhonen[7]及蒋翼迈和冯绍继[8]分别独立地建立了差分Nevanlinna值分布理论, Laine-Yang[9]得到了涉及差分多项式的Clunie引理. 应用这些理论, 许多学者对有限级超越整函数的差分多项式的值分布问题和唯一性问题进行了深入研究[10-18], 推动了复域差分值分布理论的发展.
2010年, 在文献[11]中祁晓光等得到了如下唯一性结果.
定理 A[11]假设f(z),g(z)是两个有限级超越整函数, 并且c是非零复常数. 若n≥6 ,fn(z)f(z+c)和gn(z)g(z+c)是 CM 分 担 1的, 那么 有f(z)g(z)=t1或者f(z)=t2g(z), 其中t1,t2是常数, 并且满足.
2011年, 在文献[5]中罗旭丹和林伟川得到了如下唯一性结果.
定理 B[5]假设f(z),g(z)是两个有限级超越整函数, 并且c是非零复常数. 若n>2Γ0+1 ,P(f)f(z+η)和P(g)g(z+η)是 CM 分担 1 的, 那么下列结果必有一个成立:
(i)f=tg, 其中t为常数且满足td=1 ;
(ii)f和g满足代数方程, 其中R(f,g)≡0R(w1,w2)=P(w1)w1(z+c)−P(w2)w2(z+c);
(iii)f(z)=eα(z),g(z)=eβ(z), 其中α(z),β(z)是多项式,b是使α(z)+β(z)=b成立的常数, 且满足.
定理 1假设f(z),g(z)是有限级超越整函数, 令, 其中ci(i=1,2,···,k)是互不相同的非零复常数,ti(i=1,2,···,k) 是非零常数,P(z)是一个多项式,m是集合{z:P(z)=0}的势, 且满足n≥4m+5. 如果H1(z)和G1(z)是 CM 分担1的, 那么下列结果必有一个成立:
(i) ,f=tg其中t为常数, 且满足td=1;
(ii)f和g满足代数方程R(f,g)≡0, 其中ci).
2019年, Laine在文献[18]中考虑了一类差分多项式的零点分布情况, 得到下列定理C.
定理 C[18]假设f(z)是有限级超越整函数, 记, 其中ci(i=1,2,···,k)是互不相同的非零复常数,bi(z)(i=0,1,···,k)是关于f(z)的小函数. 如果n≥2,s≥1,那么F(z)−b0(z) 有无穷多个零点.
定理 2假设f(z)是有限级超越整函数, 记, 其中ci(i=1,2,···,k)是互不相同的非零复常数,bi(z)(i=0,1,···,k)是关于f(z)的小函数,P(z) 是一个多项式,m是集合{z:P(z)=0}的势且满足n>m+1,s≥1, 那么Hn(z)−b0(z) 有无穷多个零点.
1 引 理
引理 1[4]假设f(z)为亚纯函数, 且为函数f(z) 的小函数, 则,其中

引理 2[8]设c1c2,f(z) 为不同复数,为有限级亚纯函数, 且满足σ(f)=ρ, 则对任意的ε>0, 有

引理 3如果p(z) 是一个次数大于零的多项式函数, 且存在某一复常数A, 使得

其中0, 那么一定有 degp(z)=1 .
证 明假设, 其中an,an−1,···,a0是p(z)的系数,an0, 因此有

由于p(z+c)−p(z)=A, 可得, 因此c=0 或an=0 , 矛盾.
引理 4[9]设f(x)是有限级超越亚纯函数, 其增长级为ρ=ρ(f)<∞, 且满足方程

其中U(z,f),P(z,f)和Q(z,f)是f(z)及其平移算子的差分多项式, 满足 degU(z,f)=n(≥1) ,degQ(z,f)≤n. 若U(z,f)中具有f(z)及其平移算子的最高次数的项只有一项, 则任给ε>0, 有

最多可能除去一个具有有限对数测度的例外集.
引理 5[19]设fj(j=1,2,3) 是亚纯函数, 并且满足

如果f1不是常数, 并且

其中 0≤λ<1, 并且T(r)=max1≤j≤3{T(r,fj(z))},I∗为具有无穷线性测度的集合, 那么可以得到f2(z)≡1或f3(z)≡1.
引理 6[4]设fj(z)(j=1,···,n)(n≥2)是亚纯函数,gj(z)(j=1,···,n) 都是整函数, 且满足下面三个条件:
(ii)当 1≤j 1≤j≤n1≤h (iii) 当,时, 其中E⊂(1,∞), 且E的线性测度和对数测度都有穷. 那么fj(z)≡0(j=1,···,n). 由于H1(z),G1(z)是 CM 分担 1 的, 故有 其中β(z) 为多项式. 将式(1)变形之后可得 由于 因而 同理可得,nT(r,g)+S(r,g)≤Tr,G1(z). 由式(2)和定理1的条件可得 由式(5)—(8)可得 因为n≥4m+5, 所以根据引理5可得T2(z)≡1或T3(z)≡1. 下面分两种情形讨论. 情形一若T2(z)≡1, 则 eβ(z)≡1, 那么H1(z)≡G1(z), 即 假设an是式(12)中唯一的非零系数, 因为g是超越整函数, 所以hn+1=1. 假设an不是式(12)中唯一的非零系数, 如果hn+11, 根据式(12)和引理1, 有T(r,g)=S(r,g), 矛盾, 因此hn+1=1. 同理,对任意的非零系数ak(k=0,1,···,n), 可以得到hk+1=1. 因此,f(z)=hg(z),h是常数且满足hd=1 ,其中d由定义1给出. 若t(z)不是常数, 那么由式(11)可知f和g满足代数方程R(f,g)≡0, 其中R(w1,w2)= 情形二若, 则, 即G1(z)H1(z)≡1. 假设β1,β2,···,βm是P(z)=0的根, 并且对应重数为l1,l2,···,lm, 则有 由式(13)可以得到β1,β2,···,βm是Picard例外值. 如果m≥2,βj0(j=1,2,···,m), 根据整函数的Picard定理可知,f(z)的Picard例外值至少有2个. 因此, 得出矛盾. 当m=1,l1=n时, 则存在复常数γ, 使得 那么 因为f(z),g(z)是超越整函数, 所以由Picard定理可知没有零点. 那么 其中µ(z),ν(z)是多项式. 于是 以下分两种情况进行证明. (a) 如果对I={c1,c2,···,ck}中的任意元素ci都有µ(z+ci)−ν(z) 不等于常数, 那么根据引理6,可得t1=t2=···=tk≡0, 这显然矛盾. (b) 如果I={c1,c2,···,ck}中存在有限多个元素ci, 使得µ(z+ci)−ν(z) 等于常数, 事实上, 最多存在一项这样的项. 不妨设I中存在元素ci,cj满足 其中C1,C2为常数. 根据式(16), 有 C1−C2是一个常数, 这与引理3矛盾. 因此必存在I={c1,c2,···,ck}中的某个元素cp, 使得 由式(15)和式(17)可得 先证Hn(z)−b0(z)0. 若Hn(z)−b0(z)0 , 即 对式(19)应用引理4, 则任给ε>0 , 有 另外, 再由Valiron-Mokhon’ko定理可得 由n>m+1可知式(19)不可能成立. 因此 假设Hn(z)−b0(z)仅有有限多个零点, 那么 由于 故得到 根据式(23)和Nevanlinna第二基本定理, 可得 由式(25)—(26), 有 与n>m+1矛盾. 因此Hn(z)−b0(z)有无穷多个零点.
2 定理的证明
2.1 定理1的证明






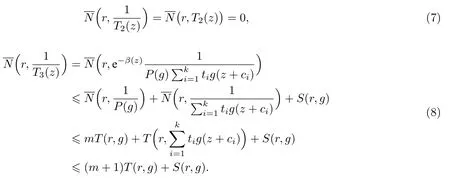


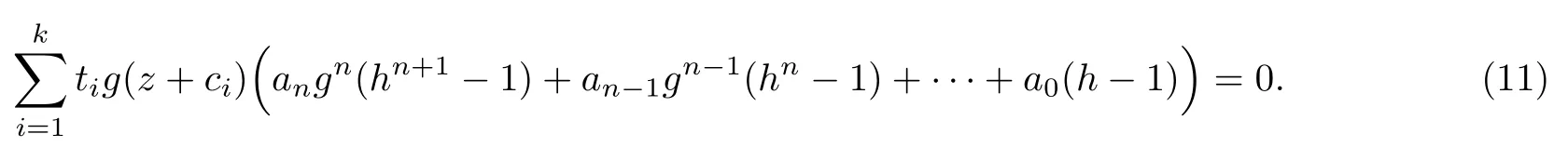



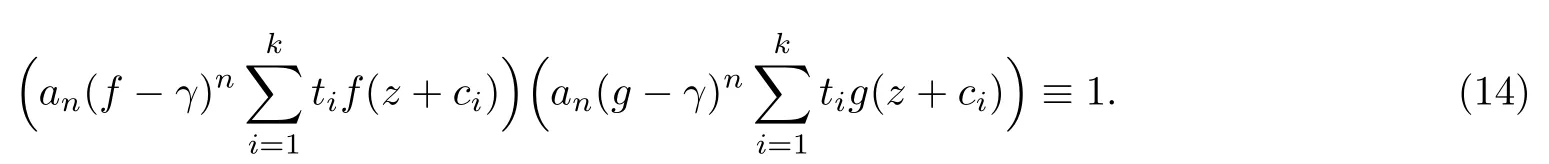






2.2 定理2的证明