风力发电机锁紧盘内外环锥角的有限元分析*
张康智, 毕永强, 曹鹏飞
(1.西安航空学院 机械工程学院,陕西 西安 710077;2.西安兴航航空科技股份有限公司,陕西 西安 710077)
0 引 言
风能作为一种对科学技术要求高,保护自然与环境的新能源,使风力发电机成为科学家与企业研究的方向。锁紧盘作为风力发电机的一个主要设备需要满足能承受较大冲击载荷与传递扭矩的要求。
Pedersen[1]利用应力基础理论公式计算得到过盈连接的径向与轴向应力,还给出应力分布图。宁可等[2]将风电锁紧盘作为实例,构建了多层过盈联接的力学模型,得到考虑承载性能和过盈层结构强度的可靠度数学模型,并以此为基础进行参数灵敏度分析。Wang等[3-6]基于过盈联接的计算方法,发明了4种风电锁紧盘的设计计算方法,形成了一套锁紧盘的设计方法与理论,并应用数值模拟等方法进行了不同方法的对比研究,开发了风电锁紧盘的应用程序,基于锁紧盘设计理论建立了考虑温度、转动的N层过盈连接设计理论。
锁紧盘内外环锥面锥角对锁紧盘的内外环摩擦力影响较大,但目前其数值缺乏相关的理论分析支撑。本文将通过有限元仿真分析,对锁紧盘过盈连接后内外环不同锥角的应力分布、变形范围、应力变化进行理论分析,并对仿真数据与理论计算数据进行比较,计算理论与仿真的误差率,作出折线图,得到内外环锥面的优化锥角。
1 锁紧盘的工作原理
风力发电机锁紧盘结构原理示意图如图1所示。锁紧盘由主轴、轴套、内环、外环和螺栓组成。为了便于装配,主轴、轴套、内环以及外环之间均为间隙配合,在工作时由轴向的螺栓拧紧力使内外环紧密结合,由外向内产生过盈量与接触压力,内环与外环、轴套与内环、主轴与轴套的配合面也由间隙配合转化为过盈配合,以传递主轴转矩。

图1 风力发电机锁紧盘结构原理示意图
图1中,d0为主轴内径,d1为主轴与轴套接触面直径,d2为轴套与内环接触面直径,d3为外环直径。
2 锁紧盘几何建模
锁紧盘装配时内外环、轴套与主轴均为回转体零件,因此可以按照轴对称方法处理问题,以简化模型[7]。本文主要研究不同内外环锥角的锁紧盘主轴与轴套过盈接触引起的应力、应变、作用力、反作用力与位移变化,取主轴与轴套接触部位建立模型。模型基本参数如表1所示。内环与外环的主要承载区域为长圆锥接触配合面。采用UG NX软件建立5个锥角不同,其他尺寸参数相同的锁紧盘模型。选取5°、4.17°、3°、2.7°与1.9°形成角度梯度,进行曲线图绘制与数值分析。

表1 模型基本尺寸参数 mm
3 锁紧盘有限元仿真分析
在装配时通过拧紧内环左端面螺栓,螺栓的轴向力转化为径向力,锁紧盘各组件由外向内产生挤压,达到过盈配合状态,挤压力主要集中于3个接触面[8]。因此,锁紧盘各组件的接触配合面将产生载荷,约束必须施加于各组件的另一圆柱面,主轴与轴套内圆面径向固定约束,在外圆面施加载荷;内环内圆面设置径向固定约束,在外圆锥面施加挤压力;外环右端设置轴向固定约束,在左端施加螺栓拧紧力。其中,装配体模型边界条件设置如图2所示。
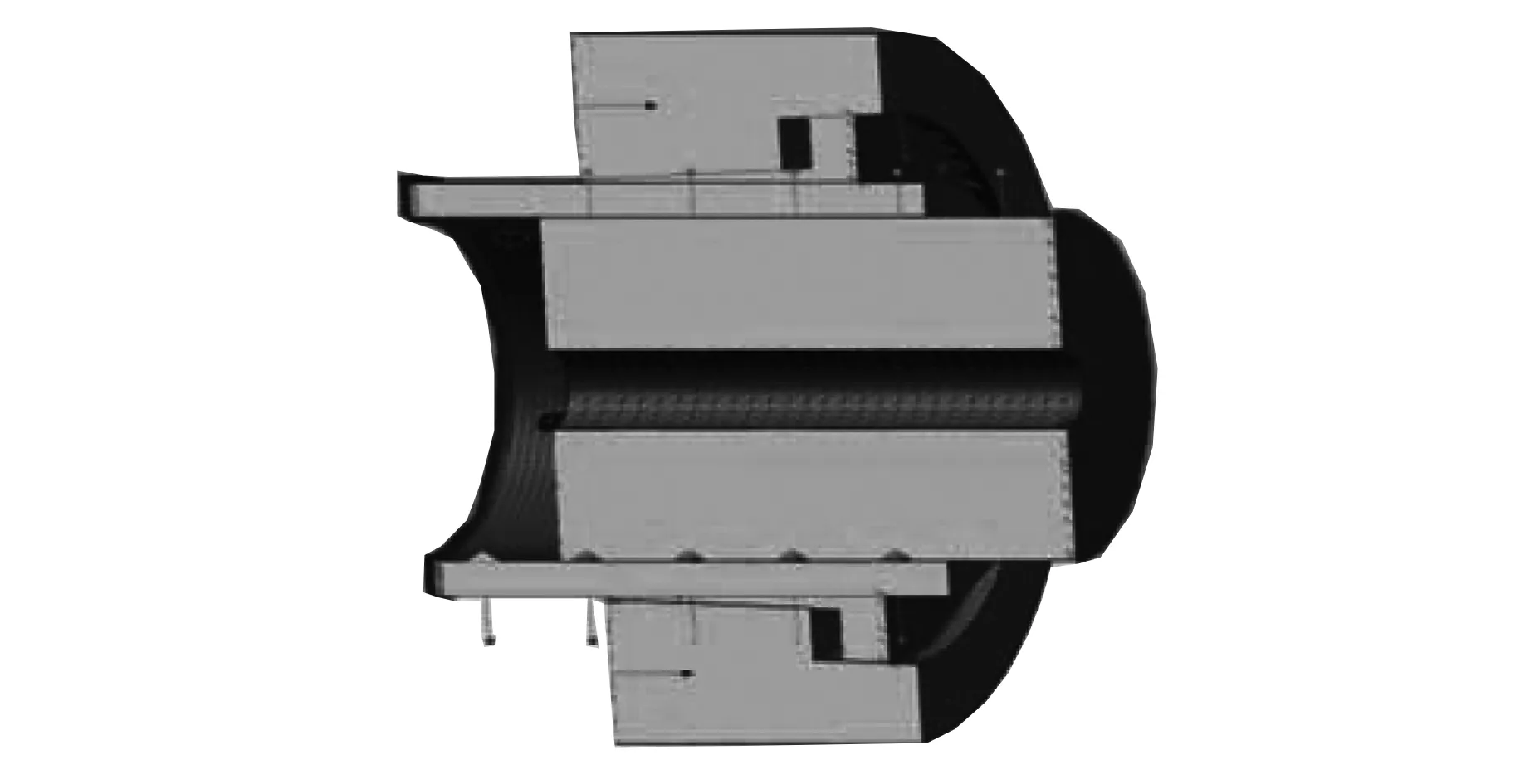
图2 装配体模型边界条件设置
建模得到组件接触面上的反作用力云图、位移云图、应变云图、应力云图、作用力云图。本文仅给出内外环锥面角度为4°13′41″锁紧盘的应变、应力、反作用力、作用力、位移云图,如图3~图7所示。
锁紧盘各组件在受到接触压力后形状与尺寸的相对改变为应变。当螺栓拧紧力卸除后,锁紧盘组件内部产生的应变能够全部恢复到原来的状态,称为弹性应变;只能部分地恢复到原来的状态,则称为塑性应变。满足使用要求的锁紧盘各组件应为弹性应变,但由于使用老化,锁紧盘会产生不可恢复的变形与磨损,塑性变形逐渐增多,直至失效。由图3可知,应变最大值集中于内外环长圆锥面与主轴、轴套的端部,这些部位是检验锁紧盘因塑性变形失效的主要部位。

图3 锁紧盘各组件的应变云图
图4为内外环锥面角度为4°13′41″锁紧盘各组件的应力云图。内环与外环采用材料为42CrMo4,屈服强度≥900 MPa。轴套采用材料为EN-GJS-700-2,屈服强度≥900 MPa。各组件的最大应力值小于其对应的屈服强度值,完全满足强度校核标准,不会发生屈服失效。由图4可知,各组件的最大应力集中于端部,在组件的中部区域,应力分布均匀连续,且应力值最小,这是由于在组件端部存在应力集中的情况。内环与外环的长圆锥左端应力最大,这是由于内外环长圆锥面的径向变形大于短圆锥面,相当于在内环与外环的长圆锥左端施加了一个逆时针扭矩。而内环与外环的短圆锥面起辅助连接作用,其对应的内环与轴套的接触面接触压力较小。

图4 锁紧盘各组件的应力云图
图5为内外环锥面角度为4°13′41″锁紧盘各组件的反作用力云图。根据牛顿第三定律可知,每一个作用力均对应着一个相等反作用力。这个反作用力即方向相反的接触压力。由图5可知,反作用力最大值位于施加力载荷的接触面,最小值位于未施加力载荷的另一面。外环的反作用力值最大,内环、轴套的反作用力值次之,主轴的反作用力值最小。这反映了由外向内,螺栓拧紧力从外环到内环、轴套与主轴进行传递时的一种衰减特征。内外环接触面是接触压力产生部位,而主轴与轴套接触面是被动受到接触压力,只要满足连接要求即可。

图5 锁紧盘各组件的反作用力云图
图6为内外环锥面角度为4°13′41″锁紧盘各组件的作用力云图。作用力即接触压力。各组件的作用力与反作用力值基本接近,但存在一定程度的误差。有限元仿真时对各组件逐个研究,且主轴与轴套的轴向长度不同,在2组件的过盈配合面施加相同的挤压力,会导致单个节点的作用力与反作用力值产生误差。

图6 锁紧盘各组件的作用力云图
图7为内外环锥面角度为4°13′41″锁紧盘各组件的位移云图。锁紧盘在装配完成之后,各组件的工作面,即过盈配合面受到挤压变形,产生过盈量,形成过盈配合。位移量基本反映了各接触面的过盈配合状况,位移最大值位于施加力载荷的接触面,最小值位于未施加力载荷的一面。外环的位移值最大,内环、轴套的位移值次之,主轴的位移值最小。这反映了由外向内,各接触面过盈量的一种变化特征,内环与外环接触面过盈量最大,是锁紧盘过盈连接的主要区域,其合理的过盈量使内外环紧密配合,达到过盈连接的要求。主轴与轴套的位移值最小,是因为该接触面不是最早产生过盈配合的位置,但其过盈量满足过盈连接要求,可以实现主轴与轴套的锁紧配合,以确保风力发电机的正常工作。同时,可以看出:主轴与轴套的中部区域位移量相同,在两侧棱边的位移量发生了突变;内环与外环的位移量从长圆锥面左端向右发生连续而均匀的递减。由此可知,内外环的长圆锥面是锁紧盘产生过盈的主要工作面,最先发生失效与不可恢复的变形,主轴、轴套的端部次之。这一特征与符合应力集中的特点。

图7 锁紧盘各组件的位移云图
由于UG NX软件放大模型在有限元仿真分析后变形程度的特征,上述云图中变形状态直观明确地表达了锁紧盘在发生失效后的形状特征。
在这些云图上,选取接触面上固定点的数值,在得到100个数据后(如表2~表5所示),选取位移量数值(即接触面过盈量),制作折线图如图8~图10所示。通过分析图8~图10可得,角度值越靠近3°,过盈量的理论计算值与仿真结果值的误差率最小。因此,风力发电锁紧盘内外环锥面角度约为3°最合适。

表2 内外环锥面角度为4°13′41″的主轴相关数值
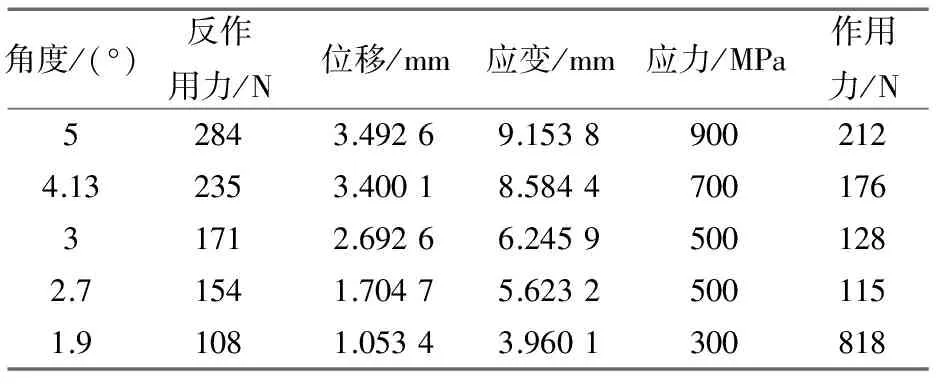
表3 内外环锥面角度为4°13′41″的轴套相关数值
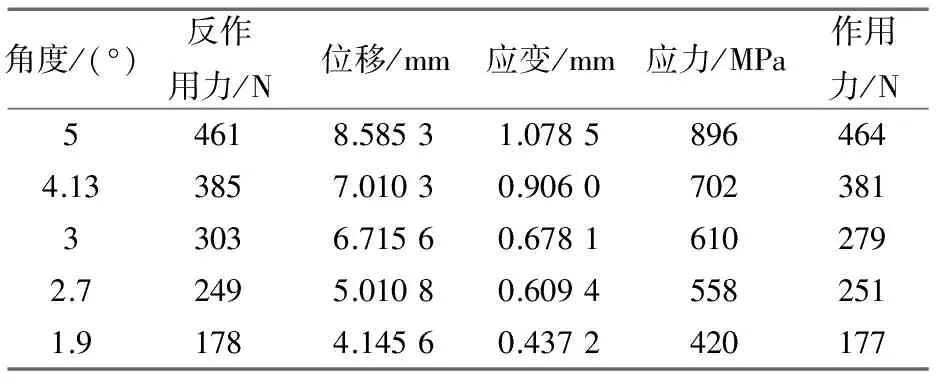
表4 内外环锥面角度为4°13′41″的内环相关数值

表5 内外环锥面角度为4°13′41″的外环相关数值
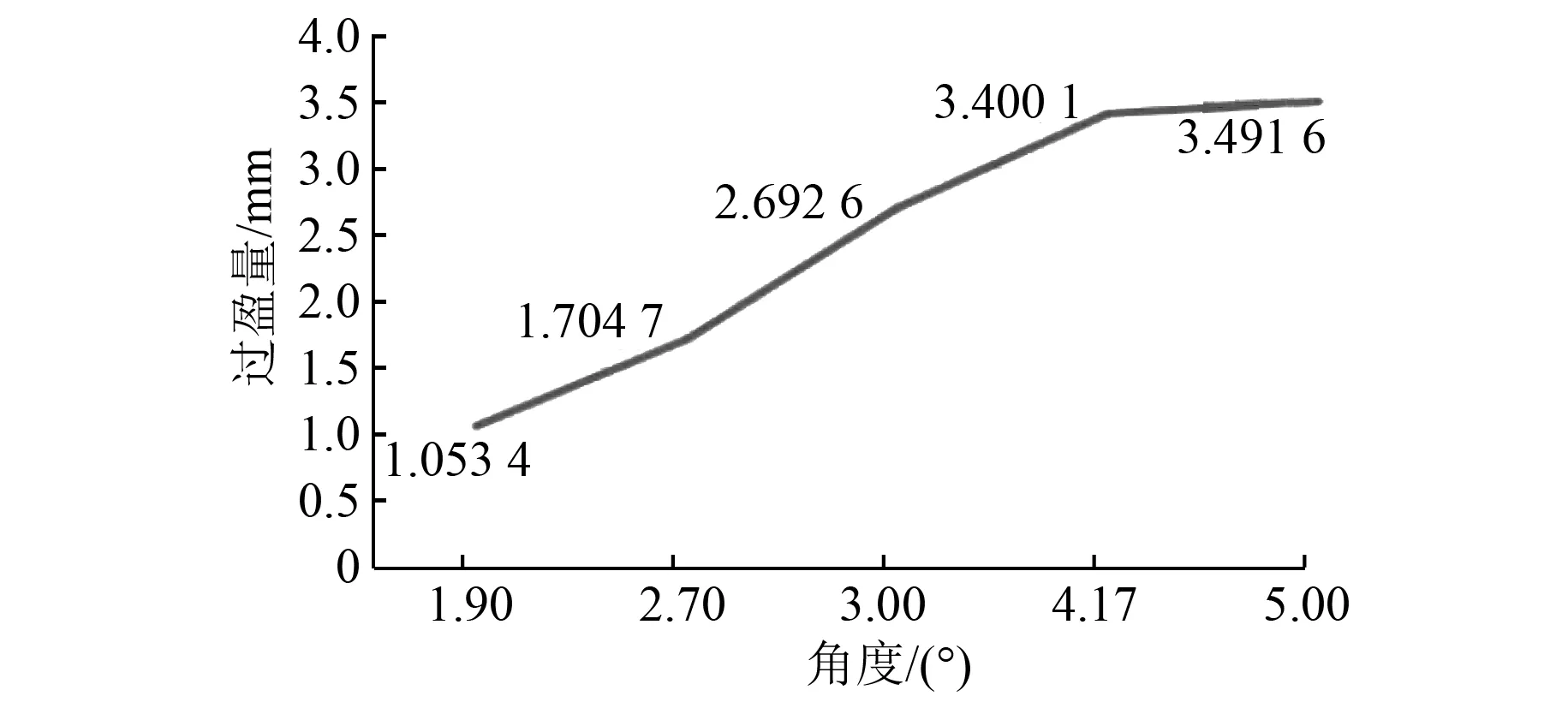
图8 主轴与轴套接触面过盈量

图9 轴套与内环接触面过盈量
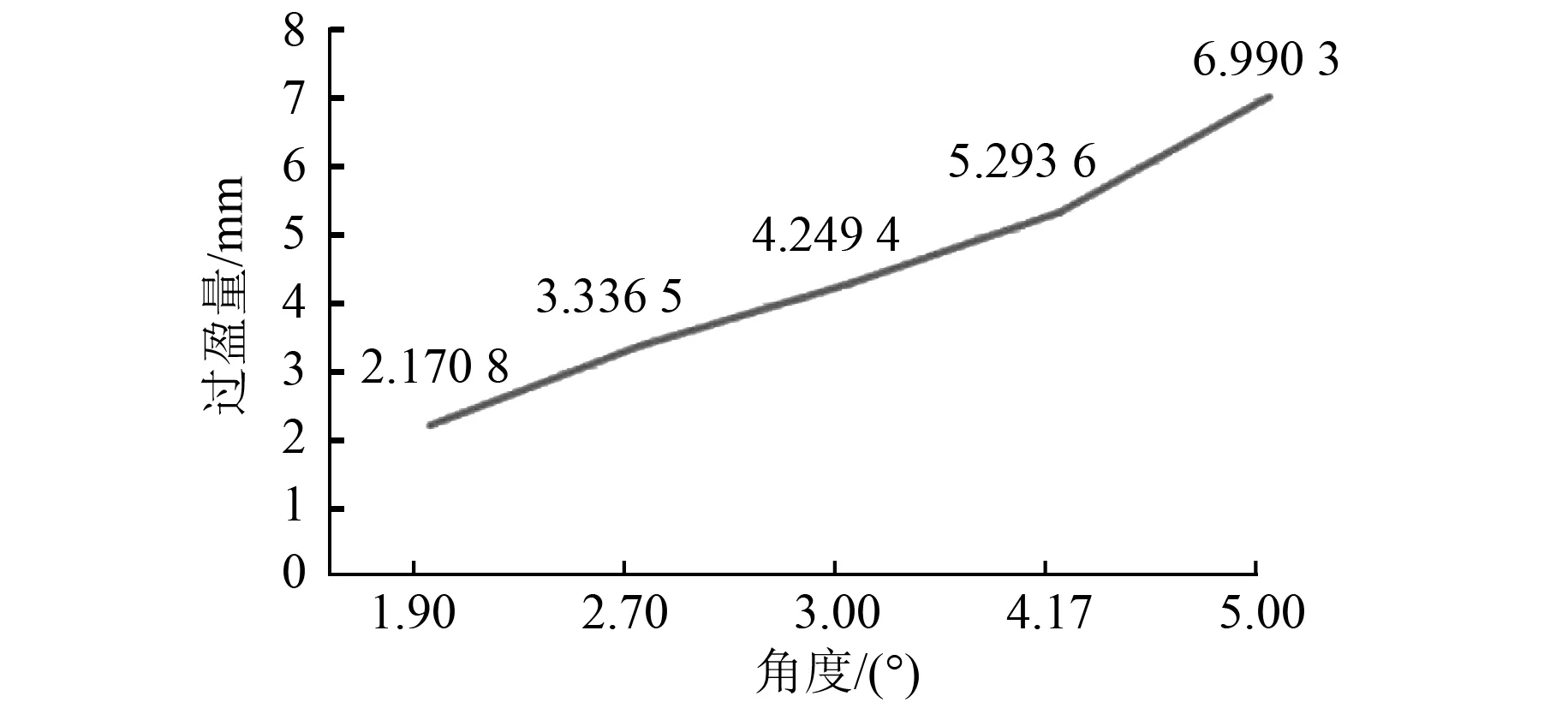
图10 内环与外环接触面过盈量
由图8可以看出,3个接触面的过盈量随内外环锥面角度的增加而增加,这种增加是趋势性的,而非纯线性增加。根据表1模型基本尺寸参数及锁紧盘过盈量计算公式[9],计算得到主轴与轴套、轴套与内环、内环与外环接触面过盈量分别为2.713、6.170、4.690 mm,将这3个数据与上述折线图进行对比可以发现,角度值越逼近3°,理论计算的过盈量值与仿真分析的过盈量值误差率最小。
一般情况,由外而内,锁紧盘3个接触面接触压力值逐渐递减,其对应的接触面过盈量值也逐渐递减。由图9可知,轴套与内环接触面过盈量明显整体高于内环与外环接触面过盈量,而理论计算中亦是如此。这是由于内环独特的锥面结构以及内外表面均受到接触压力导致的。
由图10可知,在外环与内环接触面上,过盈量关于角度变化的线性程度最高,这是由于内外环接触面是锁紧盘的主要工作面,变形程度最大与受力情况最明确。过盈量与角度值之比约为1.38,这一特性是锁紧盘今后研究的新方向。
4 结 语
本文通过对内外环锥面角度为4°13′41″锁紧盘仿真分析,得出过盈量随内外环锥面角度的增加非纯线性增加。配合件取不同的过盈量,角度值越逼近3°,理论计算的过盈量值与仿真分析的过盈量值的误差率最小。随着接触压力值逐渐递减,其对应的接触面过盈量值也逐渐递减。在外环与内环接触面上,过盈量关于角度变化的线性程度最高,过盈量与角度值之比约为1.38,这一特性将是锁紧盘未来研究的新方向。

