基于核主成分分析和深度置信网络的暂态稳定评估*

唐文权， 徐 武， 文 聪， 郭 兴

(云南民族大学 电气信息工程学院，云南 昆明 650500)

0 引 言

电力系统的规模不断扩大以及电网结构的高复杂性，准确、快速评估电力系统暂态稳定愈发困难[1]。传统评估方法分为暂态能量函数法和时域仿真法。但是前者计算量大，评估速度慢；后者在复杂系统中的能量函数难以准确计算，将产生较大偏差，导致评估准确性较差，难以满足现实要求[2]。通过人工智能方法进行暂态稳定评估可以摆脱特定的网络物理模型，避免评估过程中复杂的失稳机制[3]。该方法通过训练大量数据更新分类参数处理非线性问题，具有精度高、实时性好的优点。但上述算法基于复杂原始特征数据进行评估时，由于传统模型的泛化能力有限，需要较长时间才能满足暂态稳定评估精度的要求。

针对暂态稳定评估准确性和实时性较差的问题，众多学者进行了改进研究。文献[4]基于神经网络进行特征提取，提取出的特征能够通过暂态稳定评估模型进行检测分析；文献[5]通过二进粒子群优化算法对系统暂态数据进行分析，提取出正确反映暂态稳定性能的关键特征数据集；文献[6]基于半监督神经网络方法来判定稳定状态，提高了系统模型评估的准确性；文献[7]结合了径向基网络和Kohonen网络进行稳定评估，对比几种不同的神经网络性能。上述方法对评估模型以及特征提取方法进行改进研究，提升了暂态稳定评估性能，但分析处理高维数据时，由于浅层模型的特征提取能力受限，影响了数据特征提取效果，降低了评估的准确率。

本文提出了一种基于核主成分分析(KPCA)结合深度置信网络(DBN)的暂态稳定评估方法。根据测量的反映网络结构、运行状态和暂态稳定的电气物理量等相关特征，构建46维特征量作为原始数据特征集，然后对基于核主成分分析的特征向量进行降维，将降维后的特征向量输入到DBN网络中进行训练测试。新英格兰39节点系统仿真结果表明，该方法能有效减少暂态稳定评估的数据维数，降低评估错误率和评估时间。

1 核主成分分析法

电力系统是一个非线性系统，故障发生后，线路物理量参数为非线性关系，用传统线性方法处理非线性参数时计算效率较低[8]。因此，应考虑电气参数特征的非线性降维。KPCA利用核函数的思想引入非线性映射函数，将原始样本的空间映射到高维空间，在高维空间中进行特征降维。

对于给定矩阵X=[x1,x2,…，xn]，向量xi∈Rm，非线性特征映射：Rm→H，其中H是一个表述特征的希尔伯特空间，在特征空间H上得到Φ(x)=[Φ(x1),Φ(x2),…，Φ(xn)][9]。当Φ(xi)的均值为零时，特征空间H上协方差矩阵的样本表示为

(1)

然后计算Φ(x)中的线性主成分，得到：

(2)

定义K=Φ(x)TΦ(x)，K=(kij)n×n，kij=Φ(xi)Φ(xj)，其中K是正半定核矩阵，核函数可以计算在特征空间H上的内积，不需要得到映射函数Φ(x)，得到：

(3)

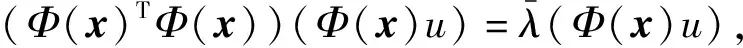
(4)

Z=wTΦ(x)=uTΦ(x)Φ(x)T=uTK

(5)

主成分分析过程中，核函数的选择尤为重要，常用的核函数有高斯径向基核函数、神经网络核函数和多项式核函数[10]。其中，高斯径向基核函数计算简单，分类效果好，因此将高斯径向基函数作为核函数。计算如下：

(6)

2 深度置信网络

DBN由Geoffrey Hinton在2006年提出，其结构如图1所示[11]。DBN网络结构是由多个受限玻尔兹曼机(RBM)和一个监督反向传播网络组成的概率生成模型，用于建立观测数据和标签之间的联合分布[12]。训练过程包括预训练和微调，预训练过程为无监督RBM从下到上逐层进行训练，将底层RBM隐含层的输出作为上层RBM可见层的输入；微调过程为将BP网络的训练和实际分类状态与预期分类状态进行比较，得到误差并向下传播，对DBN参数进行微调。

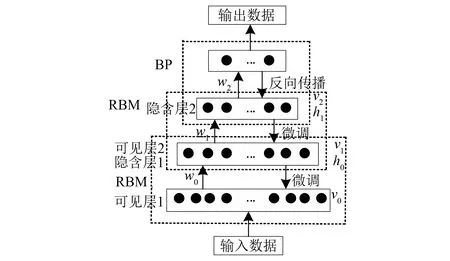
图1 DBN网络结构

2.1 预训练处理

RBM结构由可见层和隐藏层组成，两层之间的神经元采用双向连接方式，如图2所示，v和h分别代表可见层和隐含层，w为连接权重，同层之间各神经元不连接[13]。元素为二进制变量，变量的状态值为0或1。

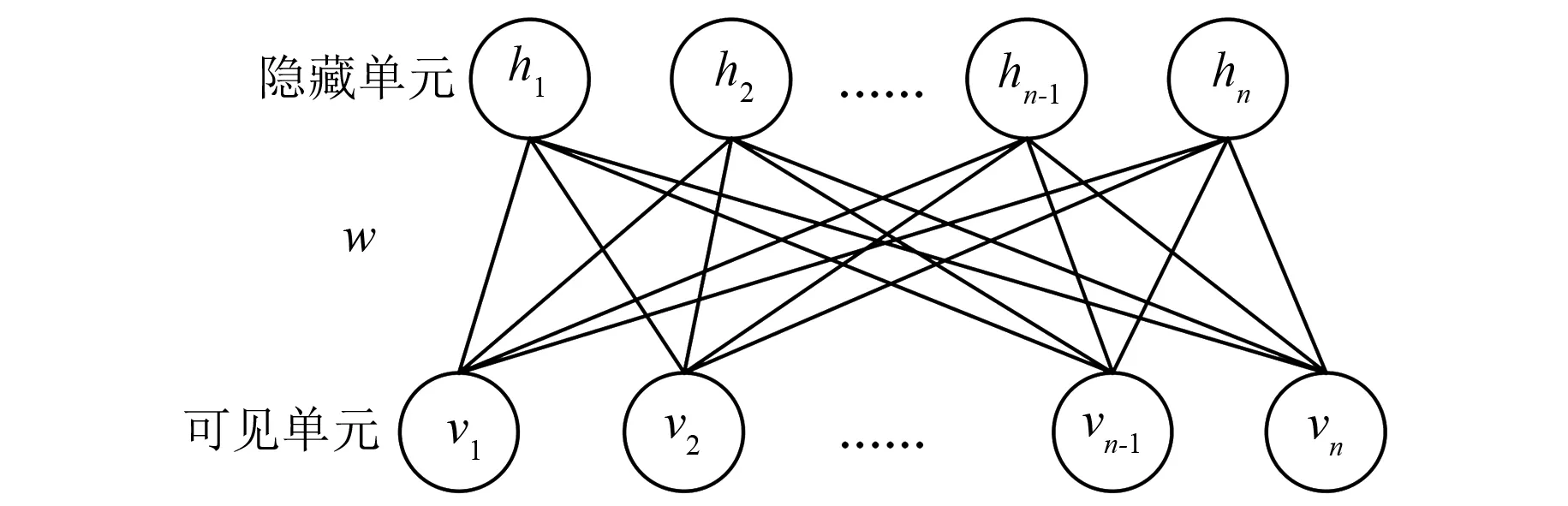
图2 RBM网络结构

对于特定的集合(v,h)，RBM能量函数为

(7)

式中：θ为模型参数，θ=(w,a,b)；ai、bj分别为可见单元和隐层单元的偏置；vi和hj分别为可见单元和隐层单元的状态；wij为vi和hj的连接权值[14]。

该网络状态概率服从正则分布，对于任何组合(v,h)，其联合概率分布为

(8)

其中：Z(θ)=∑v∑hexp(-E(v,h|θ))是标准化项。

由于同一RBM层的神经元各不连通，各隐含层神经元的激活状态相互独立，则第一个隐含层神经元的激活概率为

(9)

式中:σ(x)为sigmoid函数，σ(x)=1/(1+exp(-x))。

则第i个可见单位vi的激活概率为

(10)

RBM通过训练和学习参数值对给定的训练数据集进行拟合(w,a,b)，假设样本个数为M，通过对训练集取最大对数似然函数得到近似参数，则有：

(11)

利用比散度算法得到：

Δwij=η(data-model)

(12)

Δai=η(data-model)

(13)

Δbij=η(data-model)

(14)

式中：η为期望训练的学习率；data为训练数据的分布期望；model为RBM 模型定义的期望[15]。

采用吉布斯一次性采样数据分布作为模型定义的分布定义，利用上述定义的RBM算法，逐层训练所有RBM网络结构。

2.2 微 调

BP网络是DBN网络中最后一层，训练分为2部分：(1)接受上层RBM的输出特征向量，得到预测的分类状态；(2)将实际分类状态与期望分类状态进行比较，得到误差，并向下传播误差，对DBN参数进行微调。

3 电力系统暂态稳定评估

通过仿真获得的大量数据样本，将其作为输入特征集，随机划分为训练数据和测试数据，利用训练数据训练DBN网络的暂态稳定评估模型，然后利用测试数据对模型的性能进行测试和评估。

3.1 稳定裕度等级划分

利用发电机转子功角来判断系统暂态稳定状态Tm，计算过程如下:

(15)

式中：Δδmax为系统任意2台发电机的最大相对功角差，若Tm> 0，判定系统暂态稳定；若Tm=0，则处于临界稳定状态，否则判定为暂态失稳。

结合效用理论对系统稳定严重度等级进行划分，给定阈值α，通过比较稳定裕度Tm和阈值α，判断系统状态。

(1)若Tm>α，判定系统没有暂态失稳风险，处于绝对稳定状态，严重度指标值为0；

(2)若Tm处于[0，α]区域中，通过下式计算得到严重度指标值K：

K=a1e-Tm+a2

(16)

(3)若Tm<0，判定系统暂态失稳，此时严重度指标值为3。

通过分析可知，系统的暂态稳定严重度函数在定义域内是一直连续的，因此严重度函数必然经过边界点(α，0)和(0，3)，代入到式(16)中计算得到a1、a2值，得到新的严重度函数如下：

(17)

根据分析结果得到所有裕度Tm各个范围内的严重度函数如下:

(18)

针对电力系统运行复杂情况，对评估分析的系统稳定严重度划分5个等级，用Ks表示。严重度等级划分过程如下：

(19)

其中，当Ks值为0、1和2时，说明系统处于暂态稳定状态，且稳定裕度较高；当Ks值为3时，表示系统处于稳定与不稳定边界区域，系统稳定得不到保障，稳定裕度较低；当Ks值为4时，表示此时系统已处于暂态失稳或临界稳定状态。对此，将严重度指标为3和4的情况及时反馈给电力系统调度人员，进行故障预防排查处理，维护系统安全稳定运行。

通过划分系统暂态稳定等级，确定系统的稳定裕度，实现定性以及定量分析。

3.2 建立输入特征数据集

暂态稳定评估的一个重要步骤是构造合理的特征量。分析现有文献的特征指标，包括支路的有功功率、无功功率以及支路电流，还有节点的有功功率和无功功率，发电机的无功功率，节点电压的幅值和相角[16]。实际电网中的支路数和节点数均很大，如果将整个网络的所有特征量直接作为输入，会造成维度灾。选取以上8个特征的统计量作为输入，具体特征量如表1所示。构造了46维的特征，1～12是故障发生前的稳态特征，反应了电力系统运行方式的影响；13～23是故障期间的电气特征量特征，反应系统功率平衡被破坏所造成的影响；25～36为故障清除时刻对暂态的影响；37～46表示故障清除过程中功率不平衡对暂态稳定的影响。

表1 46维特征量

利用KPCA对46维特征数据集进行降维，有效消除冗余特征，降低网络输入的特征维数，提高了算法的效率。

3.3 基于DBN的暂态稳定性评估

DBN网络整体评估步骤如下。

Step 1：在分析处理原始数据前，需要进行归一化预处理，归一化方法为

(20)

其中：xij表示第i个样本的第j个特征，归一化处理不会造成数据偏差，能精确保存数据中所有特征之间的关系。对原始数据样本随机划分，分为训练样本和测试样本。

Step 2：利用发电机转子功角来判断系统暂态稳定状态Tm，根据系统在故障期间的参数信息进行分析，不仅得到系统的暂态稳定状态，还进一步划分暂态稳定等级。

Step 3：预训练处理，将原始特征训练数据按照自底向下的方式逐次训练每一层RBM网络结构参数。每层RBM网络中，wk根据第k-1层计算得到的数据构建，通过式(9)和式(10)计算各个单元的状态。

Step 4：微调处理，将标注的样本特征数据集作为DBN网络模型的输入，训练优化网络参数，将发电机最大相对功角差作为输出指标。选择交叉熵作为代价函数，通过梯度下降方法不断微调模型参数，直至迭代次数达到限定值。

Step 5：通过测试数据检测训练得到的DBN网络，为了满足电力系统暂态稳定评估准确性和实时性的要求，采用错误率和测试时间来衡量 DBN网络性能指标。

4 仿真分析

利用BPA软件对新英格兰10机39节点系统进行仿真验证，系统结构如图3所示。设置负载模式分别为额定负荷的80%、85%、90%、95%、100%、105%、110%、115%、120%，故障为三相短路，故障发生时间为0.2 s，清除时间为0.4 s。从上述仿真模拟结果中，选取4 000个有效样本，其中稳定样本2 251个，不稳定样本1 749个。

图3 新英格兰10机39节点系统结构图

4.1 KPCA特征降维

采用KPCA算法对模拟得到的4 000个样本进行降维。通过对46维特征数据根据累计方差贡献率≥99%进行分析，提取出13个数据变量，各主成分的特征值、方差贡献率、累积方差贡献率如表2所示。

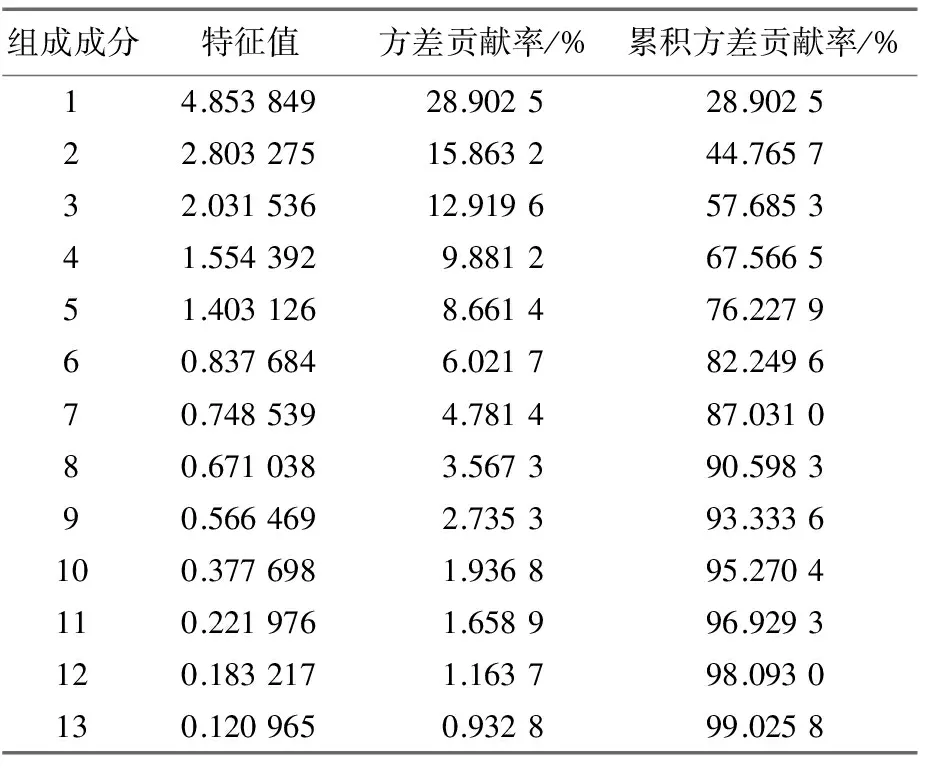
表2 主要成分信息

由表2结果可以看出，第13个主成分的方差贡献率已经很小。对比降维效果信息与保留信息，发现主成分方差贡献率最大的13个主成分可以代表99%以上的原始数据。

根据主成分方程计算得到各个主成分与特征数据的关系：

(21)

式中：bij为影响权重；Xi为系统的特征数据。

通过式(21)进行特征提取，根据表2结果可得前13个特征信息已能代表原始数据中99%的特征，因此分析了前13个特征信息Y1～Y13，在统计特征提取结果中，对特征占比较小的因素进行忽略删除，用省略号代替，则各个主成分与对应的特征指标关系为

Y1=0.932 6X44-0.274 5X43+0.163 2X8+…

Y2=0.928 3X43+…

Y3=0.736 2X19+0.658 9X20+0.632 8X21-

0.237 1X25+0.184 3X6+…

Y4=0.853 2X37+0.742 1X38+0.548 9X39+

0.146 6X6-0.109 2X36+…

Y5=0.736 8X44+0.117 3X4-0.103 5X29+…

Y6=0.853 7X44+0.242 6X15+…

Y7=0.782 5X40+0.698 1X41+0.663 2X42-

0.216 3X27-0.137 6X24

Y8=0.853 2X25+0.736 4X26+0.692 1X27-

0.167 4X22+…

Y9=0.736 5X6-0.259 8X29+…

Y10=0.674 3X5+0.223 7X21-0.135 8X27+…

Y11=0.532 1X37+0.428 3X38+0.376 5X39-

0.137 6X29+…

Y12=0.643 5X43+0.173 6X30+…

Y13=0.683 7X5-0.125 6X24+…

根据表2结果，结合系统具体特征，例如在Y1中占比最大的特征参数为X44为支路无功功率的变化特征，对系统所有支路无功特征进行比较，其中支路14～15传输无功较多，从而将其作为第一个主成分；另外，如Y3特征信息中包含了3个特征比重较大的参量X19、X20和X21，对于多个特征参量，综合考虑这3个特征信息，得到29号节点电压幅值变化较多，上述Y1～Y13的特征信息结合表1中的46维特征，保留比重较大的特征信息，各个主成分对应的关键特征如表3所示。

通过表3可以看出，影响暂态稳定过程的特征变量中主要是系统各个支路传输的有功、无功功率以及节点电压变化特征，其中故障期间各个支路传输的有功功率和无功功率所占成分最多，影响最大。这主要是因为在暂态过程中发生短路故障导致系统功率分布变化较大，各条支路传输功率变化较大，显著影响了系统暂态过程。

表3 各个主成分对应的原始特征

根据结果分析可知，在保留原始数据99%以上信息的情况下，前13个主成分可以代表99%以上的信息，将维数从46维降至13维，大大提高了算法的计算效率。

4.2 DBN训练结果分析

将4 000个原始数据样本集随机划分为3 000个训练样本和1 000个测试样本，KPCA提取的13维特征样本集进行训练分析。DBN隐层结构设置为25-20-8，学习率设为1，动量为0.5，监督训练次数为100，训练步骤为50，然后搜索合适的DBN网络参数。DBN网络的不同无监督训练次数仿真结果如图4所示。

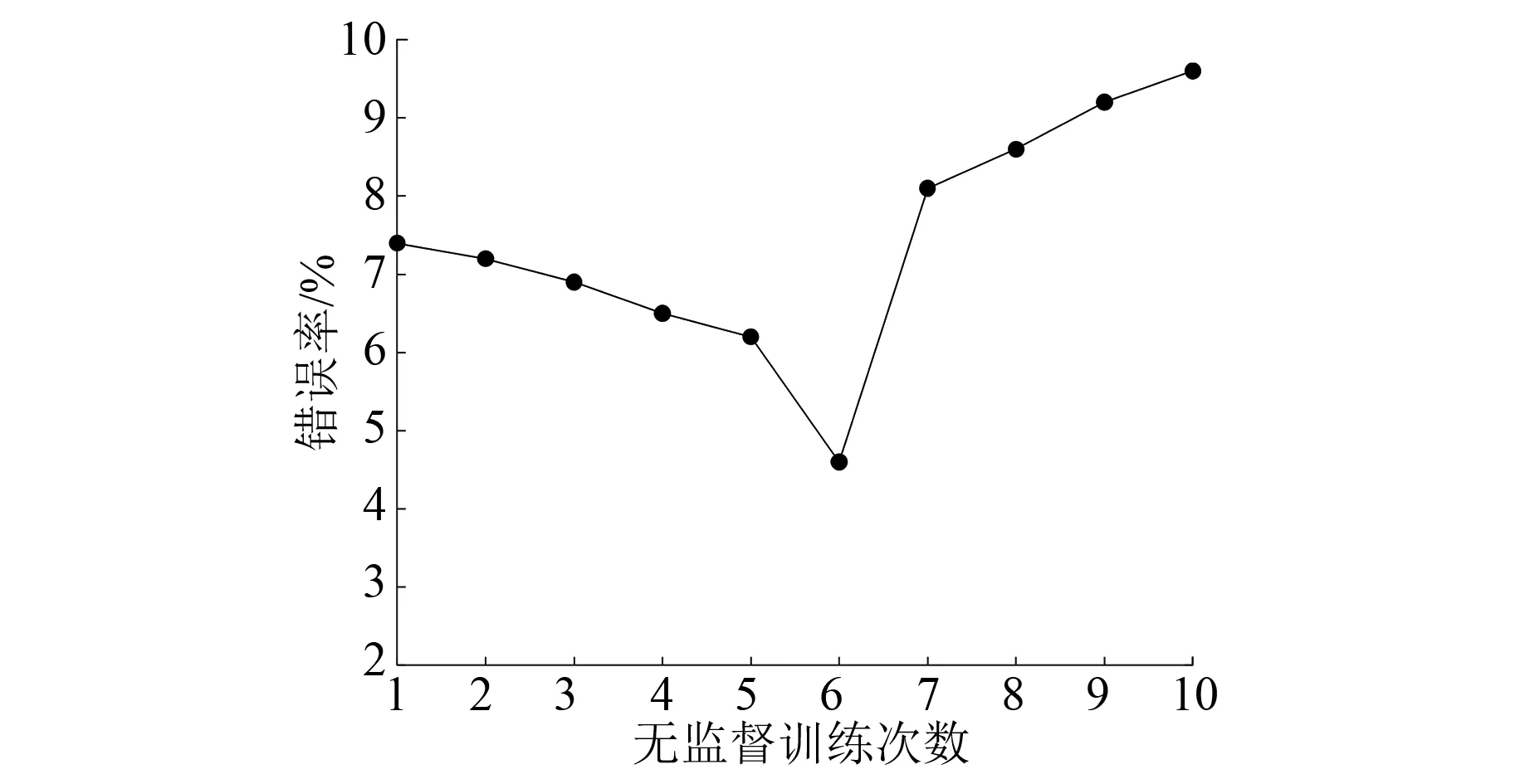
图4 不同无监督训练次数仿真结果

根据图4可知，无监督迭代次数增加，暂态稳定评估的错误率呈现先减小后增大的趋势。当无监督迭代次数较小时，原始数据的特征提取效果并不明显，错误率较高。随着次数的增加，特征提取效果逐渐变好，错误率下降。当迭代次数达到6次时，错误率达到4.6%的最小值。在6次之后，错误率随着迭代次数的增加而增加，这是由于过度提取特征导致一些重要的特征信息丢失，从而导致评估错误率上升。因此，根据DBN网络训练分析结果，采用6次无监督迭代次数。

通过无监督训练网络模型参数，通过仿真测试得到在1～10次范围内训练次数为6次时，网络模型的错误率为最低，此时模型性能最优。

4.3 网络性能分析

将融合算法与其他学习模型方法进行对比分析，考虑堆叠降噪自动编码器(SDAE)和支持向量机(SVM)，评估对比结果如表4所示。

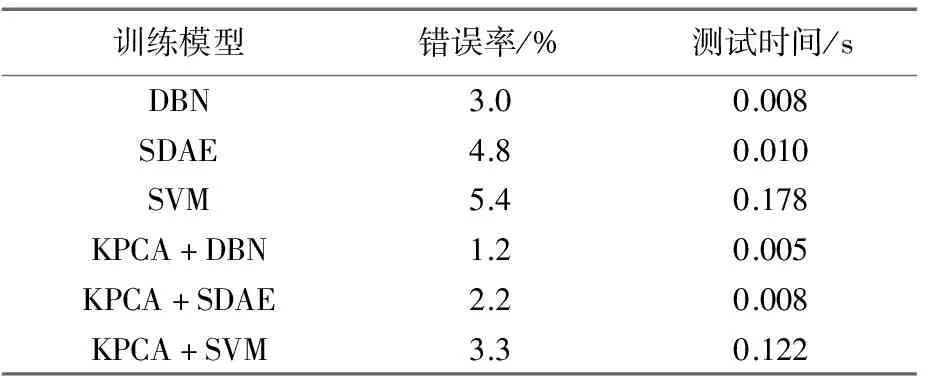
表4 暂态稳定性能评估结果

根据表4结果可知，KPCA特征降维处理后的结果对比未处理前，各模型的评估错误率平均降低了约2%，说明KPCA降维消除了数据中的冗余成分，提高了分类精度。经过KPCA降维后，每个模型的测试时间减少，这表明KPCA降维更有利于满足瞬态系统的暂态稳定评估的要求。对比不同模型的评估结果，DBN网络评估错误率(1.2%)低于SDAE和SVM，测试时间(0.005 s)也远小于SDAE和SVM，有效提高了暂态稳定评估的准确性和实时性。

5 结 语

本文提出了一种基于KPCA结合DBN网络的暂态稳定评估方法。新英格兰10机39节点系统仿真结果表明，该方法可以去除冗余特征，具有错误率低、测试时间短等优点。对比SDAE和SVM网络，暂态稳定评估错误率更低，测试时间更短。提出的基于KPCA结合DBN的暂态稳定评估方法，在评估准确率和实时性能上更优，能满足电力系统暂态稳定精度和实时性的要求。