张量表达下的多模态交通缺失数据补全算法

胡 雪，彭敦陆

(上海理工大学 光电信息与计算机工程学院，上海 200093)

1 引 言

近年来，汽车数量的快速增长导致道路拥挤现象越来越严重，对交通管理的智能化迫在眉睫.行车数据是进行智能交通网络规划、避免拥堵等应用的基础，完整的数据有利于提取有价值的交通信息.然而，实际采集的真实数据，由于检测器故障、通信处理错误等各种因素，往往使得来自多源感知设备的交通数据产生丢失的情况，甚至在一些情况下非常普遍[1].同时，高速公路摄像头(监控视频、图像等)、流量检测器等所采集的多模态交通数据，其编码方式、语义、标识存在差异，导致了信息无法融合，形成一个个信息孤岛.如何高效地实现多模态交通数据缺失值补全具有明显的现实应用意义.

国内外学者提出了许多交通数据缺失的补全方法.研究人员最初将历史(最近邻)归责方法[2]应用到交通数据补全上.随后基于主成分分析提出了大量数据补全方法，如贝叶斯主成分分析(BPCA)[3]和概率主成分分析法(PPCA)[4].作为一种能够综合表达数据的工具，近年来张量在数据处理领域中快速发展，尤其是在交通数据处理和挖掘领域应用越来越广.Acar[5]等人提出了用加权优化的CP分解(CP-WOPT) 处理缺失值，通过实验验证具有很好的性能.

尽管在单一数据源时具有较好的表现，但这些方法没有对多模态数据集合进行缺失数据补全的进一步研究.基于此，本文针对交通监控视频(非结构化数据)与车流量探测数据(结构化数据)，建立了用以描述多模态交通数据的张量模型，同时提出了基于Tucker-Crossover的多模态数据补全算法(Tucker-Crossover based Multimodal Data Imputation Algorithm，TCMD-IA).该方法融合了非结构化与结构化数据，通过张量对不同类型的数据进行统一表达，并改进Tucker分解所得的因子矩阵，将其与另一阶上所得的核矩阵进行特征融合，从而进一步提高数据补全的准确性.结合真实的多模态交通数据集实验，结果证明TCMD-IA对于多模态缺失数据的补全效果优于其他方法，且鲁棒性好.

论文其余部分的组织如下：第2部分介绍近年来交通数据缺失值估计的研究结果；第3部分给出本文所用符号的含义、张量理论基础、多模态交通数据及问题定义；第4部分给出多模态交通数据的表达和本文提出的基于Tucker-Crossover的多模态数据补全算法(TCMD-IA)；第5部分在真实数据集上进行实验，对所提算法进行有效性验证；第6部分给出论文的结论.

2 相关工作

过去几十年中，学者们提出了各种补全算法已经被应用到缺失值补全中.历史(最近邻)归责方法[2]通常用邻近几天同一时间、地点的已知数据，通过取平均值等简单操作进行填补.Qu[3，4]等人提出了BPCA和PPCA，综合考虑了交通数据的日周期性和区间变化，是解决交通流量数据估计的经典方法，并通过实验证明了其有效性.Liu[6]等人首次提出了一种基于迹范数最小化的张量补全方法(HaLRTC).他们推广了矩阵迹范数并定义了张量跟踪范数，从而将张量补全问题表示为一个凸优化问题.Zhao[7]提出了一种基于分布式减法聚类的数据填充方法，通过利用云计算技术优化聚类算法，根据聚类结果和加权距离进行填充.Han[8]等人提出了一种基于不完备集的双向聚类的算法，通过双聚类的完美簇的特性来构造属性差异矩阵，保存了对象之间的最大相似属性集，进而以双聚类的结果对缺失数据进行填补.Li[9]等人使用同类簇的均值对不完备数据进行预填充，通过形成初始完备数据集，进一步对数据集聚类，并运用同类簇的均值修正初始充填值.

在交通数据分析上，Tan[10]等人提出了多模式关联张量模型，将交通数据分为链路、周、天、小时4个不同模式，构建了四阶张量交通数据表达模型.并提出了基于Tucker分解的流量数据注入方法(TDI)，用于处理缺失数据的问题.该方法在保留矩阵模型优点的基础上，更好地挖掘了交通数据的潜在相关性.Asif[11]等人通过提取大型路网中常见的交通模式来估计缺失值，采用定点连续的近似奇异值分解、正则多进分解、最小二乘和变分贝叶斯主成分分析，提出了多种基于矩阵和张量的交通数据补全方法.Chen[12]等人将贝叶斯概率矩阵分解模型推广到高阶张量，并将其应用于时空交通数据的输入任务，通过大量实验探讨了不同的数据表示方式对归责性能的影响.Lin[13]等人提出了一种基于张量分解的张量补全算法，并在算法中引入了时空正则化约束，提高了算法的补全性能，该算法利用该代数框架对交通数据的缺失进行处理效率更高.

目前交通数据的补全研究绝大多数是针对结构化数据，对于多模态交通数据的研究相对较少，而多源的异构数据进行融合处理对于交通数据的利用十分重要.因此，在本项研究中，我们提出了TCMD-IA方法，对结构化和非结构化两种类型的数据缺失值进行补全.该方法通过构造合适的三阶张量来表达包含时空信息的多模态交通数据，结合Tucker分解，对其进行最小二乘法分解所得的因子矩阵与核矩阵进行交叉相乘，融合了不同阶之间的潜在相关信息，从而提高对缺失数据的补全效果，通过实验证明该方法的估计效果优于其他方法，且具有较好的鲁棒性.

3 准备工作

本节主要介绍多模态交通数据，并且给出下文所需张量理论基础、多模态交通数据知识，同时定义了如何对缺失数据进行补全.3.1节给出所需张量理论基础.3.2节介绍了多模态交通数据.3.3定义了本文所研究的问题.文章用到的符号以及其所代表的含义见表1.

表1 文章中所用符号其含义Table 1 Explanation of words used in paper

3.1 张量理论基础

矩阵乘积：给定矩阵A∈RI×J和矩阵B∈RJ×K，我们称C∈RI×K为A和B的乘积，用AB表示，其第(i，k)项如公式(1)所示.当A的列数与B的行数相同时，矩阵乘积才有意义.

(1)

n-Mode展开：对于张量X∈RI1×I2×…×Ir，从指定的第n阶上进行切割得到若干数据切片，其中1≤n≤r.将得到的切片以In为行，按顺序展开合并成矩阵，我们将这一过程称为张量的n-Mode展开.本文用Γ(X,n)表示张量在第n阶的展开矩阵，如公式(2)所示：

(2)

n阶模乘：给定张量X∈RI1×I2×…×Ir和矩阵M∈RIn×J，先将张量X在第n阶上进行n-Mode展开，然后将M与展开得到的矩阵相乘得到矩阵乘积，最后将得到的矩阵在第n阶上重建张量，表达式如公式(3)所示：

X×nM∈RI1×In-1×J×In+1×…×Ir

(3)

图1 Tucker分解Fig.1 Tucker decomposition

Tucker：以三阶张量X∈RI1×I2×I3为例，如图1所示，将X分解为一个核张量G∈RL1×L2×L3和3个因子矩阵U1∈RI1×L1，U2∈RI2×L2，U3∈RI3×L3，核张量G包含了不同阶之间的潜在相关性，因子矩阵U1，U2，U3可以理解为张量模型在各个阶的主成分，他们通常是两两正交的，三阶张量的Tucker分解表达式如公式(4)所示：

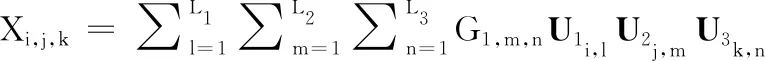
(4)

3.2 多模态交通数据

生活中，交通数据的完整性对于进一步数据分析、智能交通的优化等具有十分重要的作用，如图2所示.随着技术的发展，我们收集交通数据的方法也越来越多，道路监控数据、流量检测、GPS定位等设备都收集了成千上万的数据.这些数据由于来源的不同，导致了他们的编码方式、语义的差异，构成了信息孤岛.但来自于不同平台的异构数据，往往存在着相关性.例如对于同一路口的监控录像和车流量对于该路段的实时车况有着很高的价值，同时经过该路段的GPS数据对于我们交通规划也有很大的帮助.因此，将不同类型的交通数据通过特定的方法，本文采用张量进行融合后，将原本无法交互的信息进行统一映射，便于后续进一步挖掘交通信息的相关性，提高交通数据的利用率，这一过程对于智能交通规划、拥塞避免、智慧城市有着很大的意义.

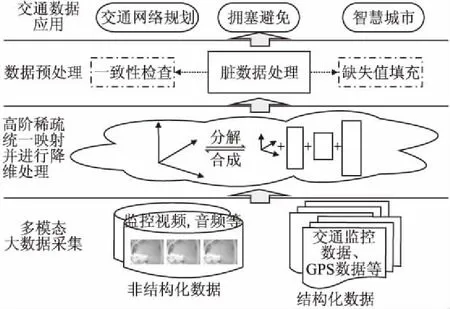
图2 多模态交通数据Fig.2 Multimodal traffic data

数据融合技术已在多传感器环境中广泛应用，目的是通过使用多源数据来获得较高的可靠性.但由于各种传感器的特点以及数据类型的差异，以更小的代价获取更高质量的信息并不是一件简单的事情.在过去的十几年中，学者们对数据融合做了较多的研究，主要包括信息融合的方法、结构、层次以及信息的表示和转换.但对于多模态交通数据的融合目前的研究本不是很多.本文针对非结构化(道路监控视频)和结构化(车流量)两大类交通数据，进行张量建模，并对其所包含的缺失数据进行补全.

3.3 问题定义

结合上文提出的多模态交通数据张量模型，我们分别用P，W∈RI1×I2×I3表示完整数据和缺失权重张量.便于分析，我们将P分成实验数据和检验数据两部分.实验数据(即缺失数据)用于验证缺失值估计的误差，用Wi1,i2,i3=0表示.已知数据用用Wi1,i2,i3=1表示，所有已知数据的集合用Ω表示，如公式(5)所示：

(5)

我们可以根据P，W得到包含缺失的实验数据集A，表达如公式(6)所示：

Ai1,i2,i3=Pi1,i2,i3Wi1,i2,i3

(6)

多模态交通数据张量化后，估计缺失数据可以视为一个张量补全问题，其目标是通过张量分解对缺失值进行估计，并且使估计值尽可能地接近真实值.用X表示填充后的数据集，那么，我们可以用公式(7)来表示目标函数：

min|P-X|，s.t.PΩ=XΩ

(7)

4 TCMD-IA

4.1 多模态交通数据的表达

结合交通数据，本文针对两种不同类型的数据进行缺失值估计：1) 非结构化数据，主要包含道路监控视频；2) 结构化数据，主要针对车流量检测数据.交通监控视频主要包括视频帧、分辨率、色彩空间等特征.其中分辨率由像素宽和高组成，色彩空间可用RGB表示.又可利用灰度值将三维RGB转化为一维灰度值.转化公式如公式(8)所示：

Gray=0.299Red+0.587Green+0.114Blue

(8)

因此，视频数据可用三阶张量T∈RIWI×IHI×IFR表示，其中IWI表示水平像素点，IHI表示垂直像素点，IFR表示视频帧数，对应的数据为该像素点的灰度值.

车流量检测数据通过道路检测设备采集，每间隔一段时间收集通过车辆数目，可根据不同时间间隔分成不同的时间片数据.根据文献[14]中提出车流量信息以天和周为时间切割单位时具有一定的循环性和相关性，因此本文构造F∈RITI×IDA×IWE来表达车流量数据，其中ITI表示一天中测试车流量次数，IDA表示按天为单位划分，IWE表示按周为单位划分，对应的每个单元数据为车流量.

得到上述两种不同类型的交通数据张量模型后，我们观察可知，视频数据的水平和垂直像素维数是固定的，帧数可随着监控时长增加.同时，车流量数据划分之后，每天的测试次数与每周的天数是固定的，测试的周数是可增加的.即T,F第一、二阶上的维度是不变的，第三阶的维度会随着时间的增加而变大.基于此，我们将上述两种不同类型数据映射到同一张量P中，在第一阶上取T,F维度之和，对其进行叠加映射.在第二阶上取T,F对应维度的较大值，较小张量的对应缺失数据置空.第三阶的维数取决于时间长短.得到融合了结构化与非结构化数据统一表达张量P.

4.2 基于Tucker-Crossover的多模态数据补全算法

上节我们已经将两种不同类型的交通数据统一映射到张量空间中，本节我们将重点介绍Tucker-Crossover模型，并将其应用到多模态张量表达下的交通数据补全上，并提出基于Tucker-Crossover的多模态交通数据补全算法(TCMD-IA).该方法利用了最小二乘法Tucker分解，计算三阶张量模型的核张量和各阶的因子矩阵.并提取核矩阵与另一阶的因子矩阵进行交叉相乘，将各阶的潜在相关性融合到因子矩阵中，使其更具有特征性，增加了缺失数据补全的准确性.

结合前文定义的P和W，构造包含缺失的多模态交通数据集A∈RI1×I2×I3，通过最小二乘法的Tucker选取合适的初始核张量B∈RL1×L2×L3.将张量进行n-Mode展开后与初始因子矩阵相乘，计算该次迭代的特征值与特征向量，排序后选取前n个特征值所对应特征向量作为因子矩阵组成.迭代至收敛，可以得到最终的核张量B和因子矩阵Ut，即算法1中的Ft.

Ft∈RIt×Lt，wheret=1,2,3

(9)

核张量B表达了各阶上数据之间的潜在相关性，因子矩阵则代表着各阶的主要特征.针对不同的数据，核张量不同.为了进一步利用各阶之间的潜在相关性，本文定义了核张量在第t阶的特征矩阵为核矩阵Ct.

Ct∈RLt×Lt，wheret=1,2,3

(10)

为了更好地利用各阶之间的潜在相关性，我们将因子矩阵Ft与下一阶的核矩阵Ct进行交叉相乘，得到特征矩阵Rt，最后结合Tucker进行张量的重建，得到的X为补全缺失值后的完整数据集.该操作再次利用不同阶之间的潜在相关性，将阶之间的特征融合到特征矩阵中，从而提高了算法对于数据补全的准确性.

Rt=FtCk，where k=(t+1)mod 3

(11)

X=B×1R1×2R2×3R3

(12)

TCMD-IA的伪代码如算法1所示.算法第1行通过缺失权重张量W构造了包含缺失的实验数据集A，如公式(6)所示.第2-12行为最小二乘法的Tucker分解，通过迭代将实验数据集分解成核张量B和因子矩阵Ft两部分.第13-18行构造了核矩阵Ct，将因子矩阵与下一阶的核矩阵进行信息融合，计算特征矩阵Rt.第19行重建完整张量，X可视为补全后的数据集.第20-22行，通过不同的评价指标对缺失值补全效果进行估计.

算法1.基于Tucker-Crossover的多模态交通数据补全算法

输入：包含完整数据和缺失权重张量P,W∈RI1×I2×I3和最大迭代次数maxIterate

输出：补全评价指标Δ

1. A←(P,W);

#通过最小二乘法Tucker分解构建核张量与因子矩阵

2. InitialU;

3. For iterate i in 1:maxIterate do

4. For order n in 1:3 do

5. U=ttm(A，U，-n);

6.U{n}=nvecs(U，n);

7. End For

8. C=ttm(U，U，n);

9. End For

10. Ttensor=ttensor(C，U);

11.N=ndims(C);#计算核张量各阶维数

12. B=Ttensor.C;

13. For order t in 1:3 do

14.Ft=C.Ttensor.Ut#因子矩阵

15.Ct=Ft(1:N{t},:);#核矩阵

16. k=(t+1) mod 3;

17.Rt=FtCk;#特征矩阵

18. End For

19. X=B×1R1×2R2×3R3;#重构张量

20. For missing item in A do

21. Δ=Eval(P，X);

22. End for

5 实验分析

5.1 数据来源

实验道路监控视频与车流量数据采集于上海市杨浦区某路段.车流量数据选取的时间节点为2019年9月1日-2019年9月30日，每天的13点-21点，以1分钟为单位采集通过车辆数，共14，400条数据.道路监控视频像素656*656，共650帧.

5.2 评价指标

(13)

(14)

错误率(Error Ratio，ER)用来度量估计后张量项的恢复误差，其表达式如公式(15)所示，值域为[0，1]，值越接近0表示数据补全的效果越接近真实值.

(15)

5.3 实验结果与分析

实验1.核张量大小对实验结果影响

实验通过设置核张量在各个阶上维数的不同，探究了核张量大小对缺失数据估计的影响.本节根据核张量各阶维数的比例，选取了[50～300，50～200，50～70]的取值范围，通过随机组合共设置了12组不同大小的核张量来探究核张量对缺失数据估计效果的影响，如表2所示.图3给出不同核张量大小对缺失数据的补全效果RMSE折线对比图.从图中可以看出，C1-C4的RMSE较大，保持在112.3左右.随着第二阶维数的增加，C5-C8的RMSE下降至110附近.C9-C12四组的RMSE相对较小，且C10所包含的数据最少.因此，在后续实验中，我们选取C10所对应的核张量大小，即[200，200，50].

表2 核张量表Table 2 Core tensor Table

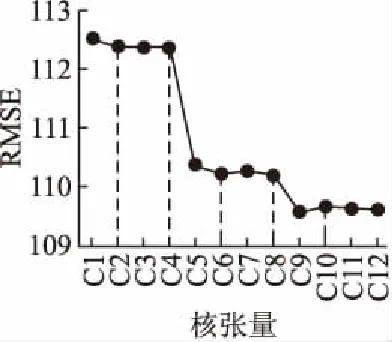
图3 核张量对补全效果影响Fig.3 Effects of core tensor on completion

实验2.与其他缺失值填充方法的比较

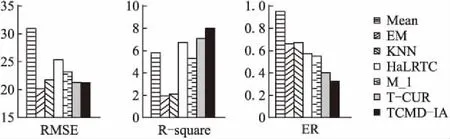
图4 不同补全方法效果对比图Fig.4 Comparison of different completion methods

实验设定P[：，：，90：100]为缺失数据，其余数据为已知数据，结果如图4所示.RMSE子图中，最大期望法的误差最小，TCMD-IA仅次于最大期望法，且与前者差距较小，平均值法的误差最大.R-square子图中，TCMD-IA的得分最大，拟合效果最好，最大期望值得分最小.ER子图中，TCMD-IA的错误率最小，平均值法最大.综合3种评价指标，我们可知T-CURE与TCMD-IA两种基于张量的方法，相比于传统方法对于缺失值处理的整体效果更佳，进一步验证了前文给出的张量在数据处理领域的表现.TCMD-IA通过Tucker分解所得的各阶特征矩阵和不同阶之间的相关性，更好地利用了已知数据，从而提高了数据补全的准确性，整体效果均优于T-CURE.

实验3.不同缺失率下的数据补全效果

实验通过选取了不同的缺失率(Missing Ratio，MR)来进一步衡量TCMD-IA对于多模态交通数据的补全效果.缺失率从10%-80%，每增加10%计算数据估计的RMSE、R-square和ER值，实验结果如表3所示.从表中可知，随着缺失率不断增加，TCMD-IA的补全效果在3种评价指标下均表现优秀，其RMSE稳定在23左右，R-square维持在0.7，ER恒定在0.3，具有较高的鲁棒性.这表明TCMD-IA在对数据补全的过程中，通过采用Tucker分解，对已知数据的比例要求并不是十分严格，仅需要少量已知数据即可进行高质量数据估计，因此更适合于缺失率较大的情况.

表3 不同缺失率下的数据补全实验结果Table 3 Experimental results of data completion under different miss rates

6 结 论

多模态交通数据的表达有利于数据的统一处理，同时，交通数据的补全可以帮助我们更好地挖掘数据的相关性和潜在价值，进一步为智能交通网络规划、避免拥堵等应用提供可靠数据.本文所提的模型将结构化与非结构化数据通过张量方法进行融合表达，并在此基础上提出了基于Tucker-Crossover的多模态数据补全算法(TCMD-IA).该方法通过Tucker分解，将因子矩阵与另一阶分解所得核矩阵交叉相乘，更好地融合了阶与阶的特征，进一步利用了不同阶的潜在相关性，从而提高算法的补全效果.在真实数据集上实验表明，文本所提算法具有更好地补全效果和鲁棒性.下一步工作将继续考虑更多不同类型的数据进行融合，提高缺失数据统一补全的效果.