基于正交试验和神经网络的液压杆稳定性研究
易 帅,孙巧雷,冯 定,周 兰,靳祖文
(1.长江大学 机械工程学院,湖北 荆州 434023;2.湖北省油气钻完井工具工程技术研究中心,湖北 荆州 434023;3.非常规油气湖北省协同创新中心,湖北 武汉 430100)
引言
液压杆位于动力猫道翻板处,当动力猫道在自动上、下管柱至钻台时,液压杆会受到较大的载荷作用,当载荷超过液压杆的临界载荷时,液压杆就会发生稳定性失效,可能导致钻井事故的发生,影响石油天然气的勘探开发,造成人员和经济的损失[1]。因此,有必要对液压杆的稳定性进行研究。SYSOEV A S等[2]对变刚度可压缩可弯曲刚性杆的稳定性问题进行了研究和解决,建立了杆件临界载荷的带根超方程体系;CAI Yong等[3]在考虑初始缺陷对杆件的影响的同时,采用了近似解法和稳定周期解的傅里叶法,从理论上分析了周期瞬态荷载作用下杆件的动力稳定性,通过对杆件不同挠度的研究,用Maple软件计算了杆件的动力不稳定性;LEONID K等[4]提出了一种利用数值解析的边界元法(MGE)求解连续梁等杆系稳定性问题的算法,并在MATLAB环境下进行了临界力的计算;冯超等[5]利用有限元软件对受压杆件的稳定性进行分析,并对其临界载荷进行了ANSYS验证;李琳等[6]以Koiter稳定性理论为研究基础,分别分析了不同约束的压杆在欧拉临界载荷作用下的稳定性;周奇才等[7]基于压杆稳定性定义,在欧拉描述方式下提出了一种轴向刚度判别法,通过对刚架模型进行数值分析,验证了该轴向刚度判别法的有效性和适用性;包卫平等[8]从强度和压杆稳定的观点对升降桅杆进行弯曲强度和压曲稳定性分析,采用能量法和等效刚度法推导出变截面压杆的刚度求解公式。
国内外学者对受压杆件的稳定性进行了广泛的理论计算分析和有限元仿真模拟[9-14]。但在实践过程中发现:由于环境因素的影响,会在液压杆上产生缺陷,如图1所示,缺陷使液压杆发生弯曲破坏的临界载荷减小,更易发生稳定性失效。所以本研究针对含有缺陷的液压杆分析了影响压杆稳定性的因素,并利用正交试验法得到了各个因素对液压杆稳定性的影响趋势及其显著性,同时利用BP神经网络建立了液压杆屈曲载荷预测模型,为含缺陷的液压杆在使用过程中的稳定性提供比较准确的预测,以减少事故的发生。

图1 液压杆上的缺陷
1 液压杆有限元计算模型
根据杆端位移的欧拉公式[15],当液压杆的材料和使用工况确定后,液压杆的屈曲载荷大小取决于液压杆最小截面惯性矩。液压杆最小截面惯性矩与缺陷的形状、深度、位置以及缺陷的面积有关,为了得到不同缺陷因素对液压杆稳定性的影响规律与影响显著性,有必要对液压杆进行数值模拟来研究缺陷与液压杆稳定性之间的关系。液压杆上出现的缺陷形状一般是不规则的,数值模拟时将缺陷的表面规则化处理为圆、椭圆、矩形。
1.1 模型建立
建立的液压杆三维模型如图2所示,材料为42CrMo,其密度为7850 kg/m3,弹性模量为206 GPa,泊松比为0.3,中间部分直径为12 mm,长度为150 mm。对现场使用的液压杆缺陷进行测量与记录,选取缺陷的深度为0.8,1.6,2.4,3.2,4.0 mm;缺陷的面积为4.5,8,12,18,25 mm2;缺陷距底端的距离为35,65,75,85,115 mm。以此为基础建立液压杆的有限元模型,对不同缺陷的液压杆临界载荷进行了有限元计算。

图2 液压杆三维模型
1.2 网格划分及边界条件与载荷
运用静态结构模块和线性屈曲模块对液压杆的临界载荷进行求解,将建立的液压杆三维模型导入有限元软件中,采用四面体单元对结构进行网格划分,由于模型的计算对计算机内存要求较高,所以网格数不宜过密,经网格无关性检查,最终的网格数约为24万,不同类型缺陷局部细化网格如图3所示。根据实际工作状况对液压杆进行约束,即对液压杆的底端进行固定约束,上端施加一轴向的压力,液压杆约束与受力如图4所示。由于有限元软件计算的临界载荷为加载值与屈曲因子的乘积,所以在液压杆上端加单位载荷,有限元分析得到的屈曲因子即为液压杆的屈曲载荷。

图3 不同类型缺陷局部细化网格图

图4 液压杆约束与受力图
2 试验设计与分析
2.1 正交试验分析
由于将所有因素全部进行有限元分析需要375次试验,为了减少试验次数且不影响试验的准确性,采用正交试验的方法对影响液压杆稳定性的因素进行分析[16]。影响含有缺陷的液压杆稳定性的因素主要有缺陷的形状、深度、位置、面积,因此,本研究选取的正交表为L25(3×53),各个因素水平表如表1所示。
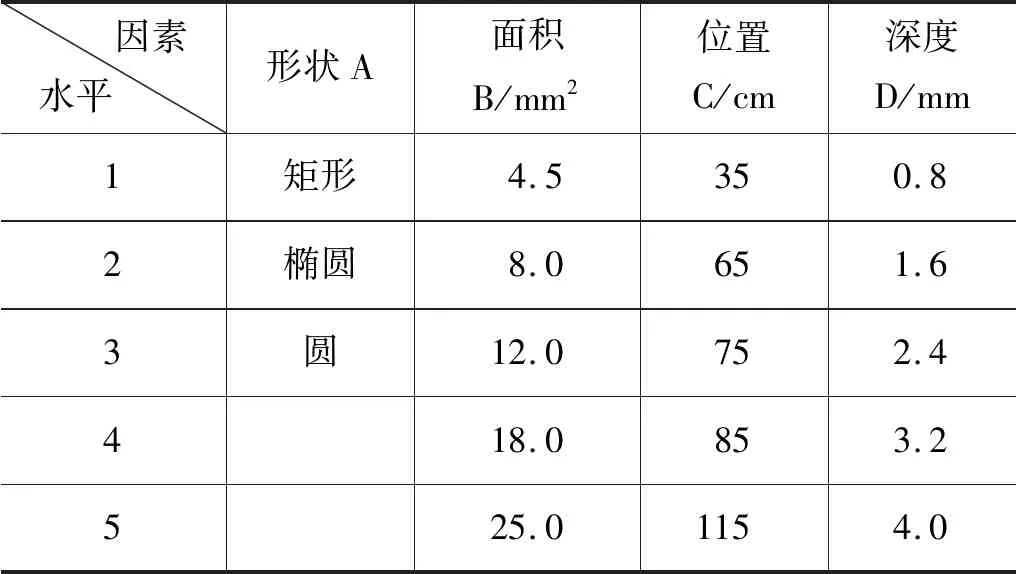
表1 因素水平表
表2为混合正交表,需要进行25次试验,对每次试验运用有限元分析软件计算液压杆的临界载荷,试验方案和有限元计算的结果如表2所示。

表2 试验方案及分析结果表

(续表2)
2.2 直观分析
由于液压杆的屈曲载荷受4个因素的影响,故需要考虑多目标正交试验结果的直观分析。运用直观分析法对试验数据进行处理如表3所示。其中,Kij(i=1,2,3,4,5;j=1,2,3,4)表示表1的第j列中水平为i对应的试验结果之和;kij为Kij的算术平均值;极差Rj=maxkij-minkij。

表3 数据分析计算表
极差Rj可以衡量各个因素对试验指标影响的大小,极差越大,表明这个因素对液压杆稳性的影响越大。从表3可以看出,缺陷深度、缺陷相对底端的距离和面积所对应的极差较大,故缺陷深度、缺陷相对底端的距离和缺陷面积对液压杆稳定性影响较大,而缺陷的形状对液压杆稳定性影响较小;由于k31
2.3 方差分析
对试验数据方差分析结果如表4所示,其中,P值表示该因素对结果影响出现不显著情况的概率,设缺陷形状、缺陷面积、缺陷位置、缺陷深度的P值分别为P1,P2,P3,P4。若P<0.01时,则表明该因素对试验结果具有高度显著影响;若0.01 表4 方差分析表 图5 液压杆屈曲载荷预测模型结构图 基于MATLAB软件,对液压杆屈曲载荷的预测模型常用3×3×1×1的BP神经网络进行训练与预测。训练样本总计37组,将正交试验中的25组作为学习样本,将缺陷面积、位置和深度进行单因素分析的12组作为预测样本。为了使模拟结果收敛且能较好地模拟预测样本,选择的神经网络误差精度为0.001,学习速率为0.01,训练次数为1000。BP神经网络预测输出与期望输出如图6所示,横坐标为仿真预测样本序号g,预测误差δ如图7所示。 图6 BP神经网络预测与期望输出折线图 从图6可以看出,12组预测输出和期望输出的变化趋势一致,预测输出的12个点在期望输出12个点附近且数值相差不大。由图7可知,该神经网络预测模型的预测值与期望值的误差在-0.1%~0.1%之间,说明根据正交数据训练的BP神经网络具有很高的精确度。 图7 BP神经网络预测误差百分比 如图8所示,在液压杆屈曲载荷的BP神经网络拟合表征中,横坐标为预测值x,纵坐标为实际值y,在神经网络训练时将数据进行了规范化,使预测值与实际值在-1~1之间。参考曲线代表预测值与实际值相等,拟合曲线的斜率为R,R值为预测输出与期望输出的相关系数,R值越接近1说明预测输出与目标输出的相关性越大,即神经网络预测模型的拟合程度越高,拟合曲线表达式为y=0.99754x+0.0031,则该液压杆屈曲载荷预测模型的相关系数R=0.99754,表明该BP神经网络预测模型能够对液压杆屈曲载荷进行很好的拟合,利用该神经网络对出现缺陷的液压杆屈曲载荷进行预测是可行的。 图8 BP神经网络误差拟合结果 为了深入验证模型的正确性,应用本研究的BP神经网络模型,对参考文献[20]相关数据进行验证和分析。该文献研究了含缺陷液压杆的屈曲载荷和缺陷的面积、位置和深度间的关系,基于该文225组实验数据,将200组作为训练样本,25组作为预测样本,对建立的BP神经网络进行训练,训练结果如图9、图10所示,横坐标为实验预测样本序号h。 图9 BP神经网络预测与期望输出折线图 从图9可以看出,建立的BP神经网络模型能够比较准确地预测含缺陷液压杆的屈曲载荷,且实验值与预测值的差值不超过150 N,所以在此范围内对含缺陷液压杆屈曲载荷的预测是可行的。由图10可知,该神经网络预测值与实验值的最大相对误差为1.002%,相对误差控制在5%以内。表明该BP神经网络模型对含缺陷液压杆屈曲载荷的预测精度较高,同时也说明缺陷的面积、位置及深度对含缺陷液压杆的屈曲载荷有重要影响。 图10 BP神经网络预测误差百分比 (1) 首先根据杆端位移的欧拉公式,得到可能影响含缺陷液压杆稳定性的因素。运用正交试验方法和有限元仿真研究了缺陷的结构与尺寸对液压杆稳定性的影响规律,发现缺陷的面积、位置、深度对液压杆的稳定性具有显著影响,且液压杆的临界载荷与缺陷面积和深度负相关,与缺陷到底端的距离正相关;缺陷的形状对液压杆的稳性影响较小; (2) 通过正交试验数据建立的BP神经网络模型对液压杆屈曲载荷仿真的预测具有很高的精确度,最大相对误差在0.1%内,且预测输出与期望输出相关系数为0.99754; (3) 将建立的BP神经网络模型通过实验数据的训练,最大相对误差为1.002%,即能够较准确地对杆件的屈曲载荷进行预测,说明该BP神经网络能够运用于现场预测含缺陷液压杆屈曲载荷,防止液压杆因载荷过大而屈曲破坏。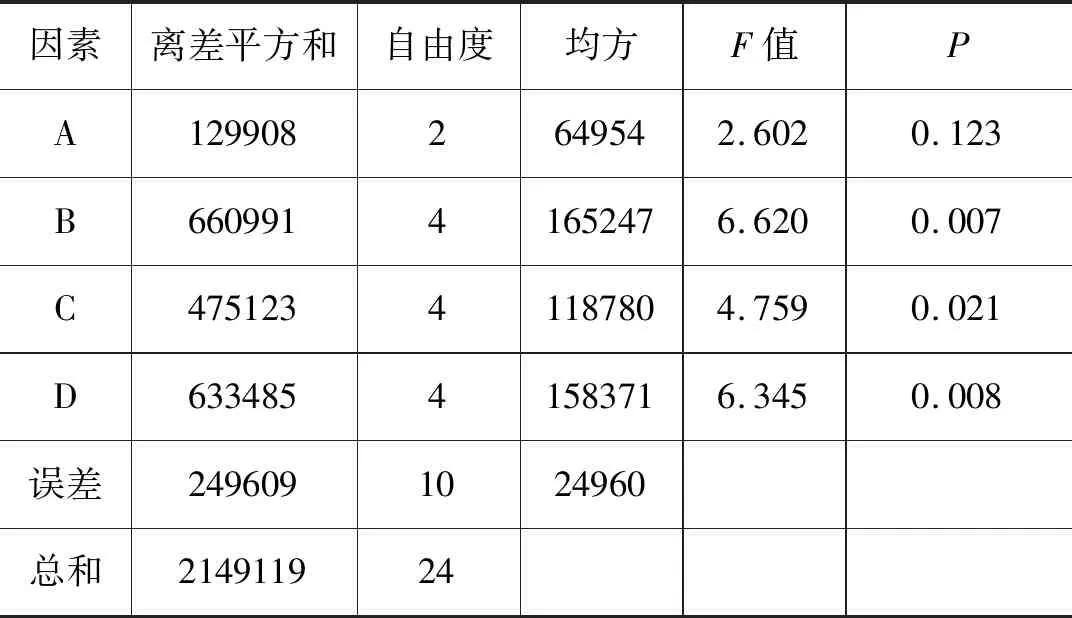
3 液压杆屈曲载荷预测
3.1 预测模型的选取


3.2 液压杆屈曲载荷的预测与检验



3.3 模型验证与分析


4 结论

