基于姿态枚举算法的混凝土布料机械臂轨迹控制
方梓帆,钱剑勇,苏 琦,徐 兵
(浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310027)
引言
混凝土布料机具有布料范围大、机动性高、灵活性强的特点,是建筑行业中至关重要的工程机械之一[1]。如今,我国混凝土布料臂架广泛采用操作工人单关节独立遥控的控制方式。为减少劳动力投入,提高浇筑质量,避免因布料机械臂支撑体系坍塌等极端情况导致的人员伤亡事故,建筑施工上对全自动混凝土布料机器人的需求日渐提高,其核心问题就是如何实现末端轨迹控制,即全自动布料[2]。
国内外已经有诸多学者对混凝土布料机械臂的末端轨迹控制进行了研究,均取得了较好的成果。KEATING S J等[3]实现了泡沫式建筑材料浇筑喷头的末端轨迹控制;AYTEN等[4]基于能量消耗最少的原则进行了最优轨迹规划方面的研究,提出了效率高且复杂度低的优化算法;黄罡等[5]基于正解模型推导了油缸行程和关节角变化的关系,并通过位移传感器测量液压缸的伸出长度,运用前馈补偿的控制策略,优化了臂架的控制系统;周淑文等[6-8]基于正解模型采用插补算法实现对臂架出料口的智能化控制,并进行了仿真与实验;杜冰晖等[9]依据最优控制原理制定了臂架运动过程中的关节角限制条件,并进行了避障控制的研究;王珊[10]将臂架的整体形态与臂架逆解相结合,使臂架保持流动阻力较小的弧形;张思奇等[11]运用最小范数法使关节运动连续平稳,并进行了联合仿真优化;郭立新等[12]采用以各执行构件变化时间最大者最小的最优化控制原理进行运动学逆解;俞志鹏[13]基于遍历算法对上个离散点关节角附近的角度进行遍历,以各关节角绝对值之和最小作为限制条件;朱云峰等[14]基于数值迭代算法,依次固定所求夹角中的3个而转动另一角,使得末端逐步逼近目标点,该方法适用于PLC控制,能够明显使臂架运动快于人工手动调试。但是上述研究多是针对布料机刚性臂架,而在实际应用中,布料机臂架末端常通过布料软管对混凝土进行导向,若臂架进行大幅度摆动,容易导致布料软管出现甩动,影响混凝土出料落点的位置。因此,在进行轨迹控制时,还应考虑最后一节臂的摆动对布料软管产生的影响。
针对混凝土布料机的轨迹控制,提出一种基于姿态枚举算法的机械臂轨迹控制方法,采用该方法对某13m-3Z型混凝土布料机进行了末端轨迹控制,并基于AMESim-MATLAB-ADAMS模型对其进行了联合仿真分析,得到了末端轨迹以及布料倾角的变化规律。该方法以布料机械臂的运动学逆解模型为基础,求解得到目标关节角度,适用于具有多自由度的布料机械臂的PLC控制。
1 混凝土布料机械臂结构与运动学模型
1.1 混凝土布料机械臂结构
混凝土布料机械臂通常是一个多自由度机械臂系统,本研究以具有三节臂的混凝土布料机械臂为例,阐述其基本结构及运动学逆解模型的建立过程。该混凝土布料机械臂结构如图1所示,其主要组成部分为回转台、1#关节、1#臂、2#关节、2#臂、3#关节、3#臂、末端软管。末端软管基本不具有混凝土承载能力,仅为末端混凝土出料口起导向作用,在施工过程中,基本保持垂直朝向工作平面,可暂忽略其自由度,因此可将该系统视为回转台+三节臂组成的四自由度系统。

1.回转台 2.1#关节 3.1#臂 4.2#关节 5.2#臂 6.3#关节 7.3#臂 8.末端出料口 9.末端软管图1 混凝土布料机械臂结构示意图
1.2 混凝土布料机械臂运动学正解模型
为研究关节补偿角对末端出料口位置的影响,以D-H矩阵法为理论基础,建立各臂段关节角度变化和臂架末端空间位姿的关系。在该混凝土布料机械臂上建立的D-H坐标系如图2所示。

图2 混凝土布料机械臂D-H坐标系示意图


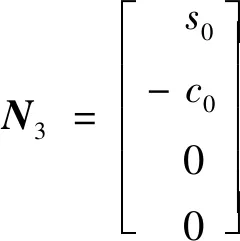
(1)
1.3 混凝土布料机械臂运动学逆解模型
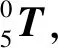
T=[N5N6N7N8]

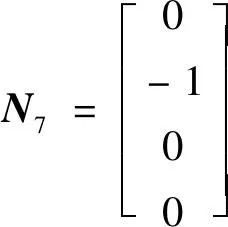
(2)
以基坐标原点为原点设置圆柱坐标系如图3所示。在该坐标系中,为便于建立末端位姿与关节角的函数关系,设定4个布料参数如下:布料高度H为末端坐标系原点在圆柱坐标系z轴方向的尺度;布料半径R为末端坐标系原点在圆柱坐标系的径向尺度;布料倾角θ为末端坐标系x轴与水平面之间的夹角;此时θ0也称布料转角。
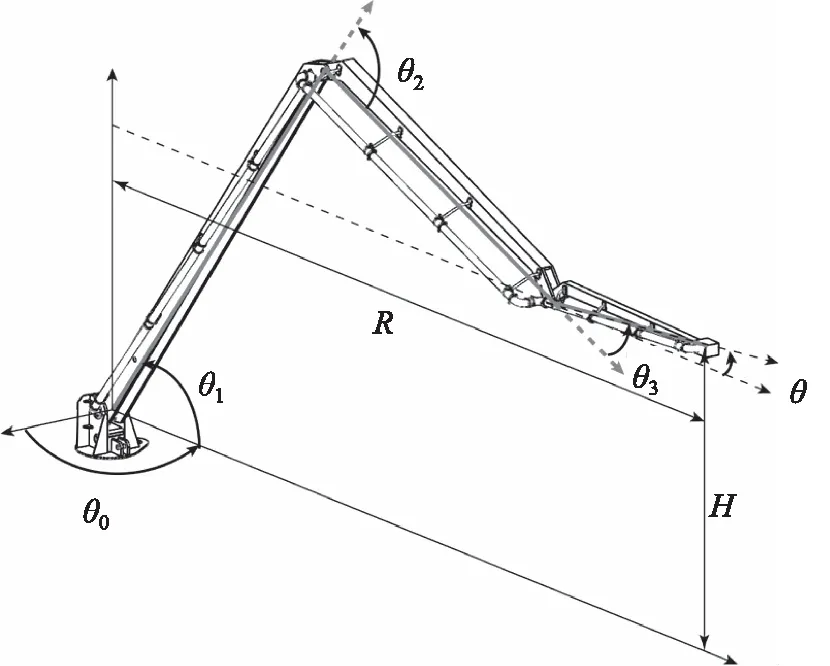
图3 圆柱系与布料参数示意图
(3)
式中,R3×3——末端旋转矩阵
P3×1——末端位置矢量
经过降维简化处理后,根据末端旋转矩阵、末端位置矢量的数值意义可建立二维平面内3个关节角与4个布料参数的关系如下:
即:
(5)
整理可得混凝土布料机械臂逆运动学求解方程:
(6)
得到3个关节角和设定的4个布料参数之间的关系:
(7)
2 基于姿态枚举算法的混凝土布料机械臂轨迹控制方法
2.1 姿态枚举算法的思想及步骤
本研究所提出的基于姿态枚举算法的混凝土布料机械臂轨迹控制方法,其目的在于减小布料倾角θ的变化量,进而减少末端软管相对于3#臂架铰点的转角变化量,降低混凝土出料时因末端软管径向甩动产生的离心力。
现以某13m-3Z型混凝土布料机械臂为例对该控制方法进行阐述,部分参数如表1所示。

表1 13m-3Z型混凝土布料机械臂参数
令笛卡尔坐标系原点、z轴、x轴分别与圆柱坐标系原点、z轴、方位角基准轴重合,可建立笛卡尔坐标系中布料参数与臂架末端位置的关系如下:
(8)
当给定一段布料机械臂末端运动轨迹时,利用插值法可将该目标运动轨迹离散化为不同的离散点。通过控制臂架末端依次跟随离散点,最终实现臂架末端从目标起点经目标轨迹抵达目标终点的布料操作。离散化过程中,各离散点之间的距离应根据实际工程需要来确定。若距离过小,产生的离散点则过多,容易导致控制器运算量较大,末端频繁动作而不稳定等问题;若距离过大,则离散点过少,会使末端轨迹跟踪的精度降低。
以控制末端按照某一直线轨迹进行运动为例,给定离散点之间的距离,可求得离散点个数,并进一步确定相邻离散点坐标差值如下:
(9)
式中, Δx——各离散点在笛卡尔坐标系x轴的差值
Δy——各离散点在笛卡尔坐标系y轴的差值
Δz——各离散点在笛卡尔坐标系z轴的差值
n——轨迹路径上的离散点个数
(xt,yt,zt)——目标轨迹终点坐标
(x0,y0,z0)——目标轨迹起点坐标
布料倾角与各关节角的关系如下:
θ=θ1+θ2+θ3
(10)
对于目标轨迹上任一对正向运行的相邻离散点而言,布料半径的变化量满足下式:
(11)
根据ΔR的正负判断相邻2点布料半径的变化方向,作为末端姿态即布料倾角枚举方向的判定依据:

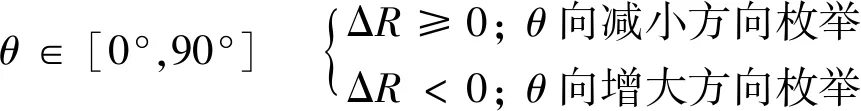
(12)
设定初始布料倾角θ以及每次枚举时的倾角变化量Δθ。为使混凝土浇筑出料顺畅,通常令θ=-90°,同时将各离散点笛卡尔坐标转换为柱坐标,即计算各离散点坐标对应R,H,θ0的值代入布料机械臂逆运动学模型,可求解得到各关节角度值。
当求解得到的θ1,θ2,θ3不满足表1所示关节角范围条件时,按照枚举方向对θ进行枚举直到其逆运动学求解结果符合范围条件。其中,目标轨迹起点到第2个离散点的求解过程流程图如图4所示。令所有离散点均按此方法求解得到相应的关节角度值从而生成预设路径,即完成了本研究所提出的基于姿态枚举算法的混凝土布料机械臂轨迹控制。
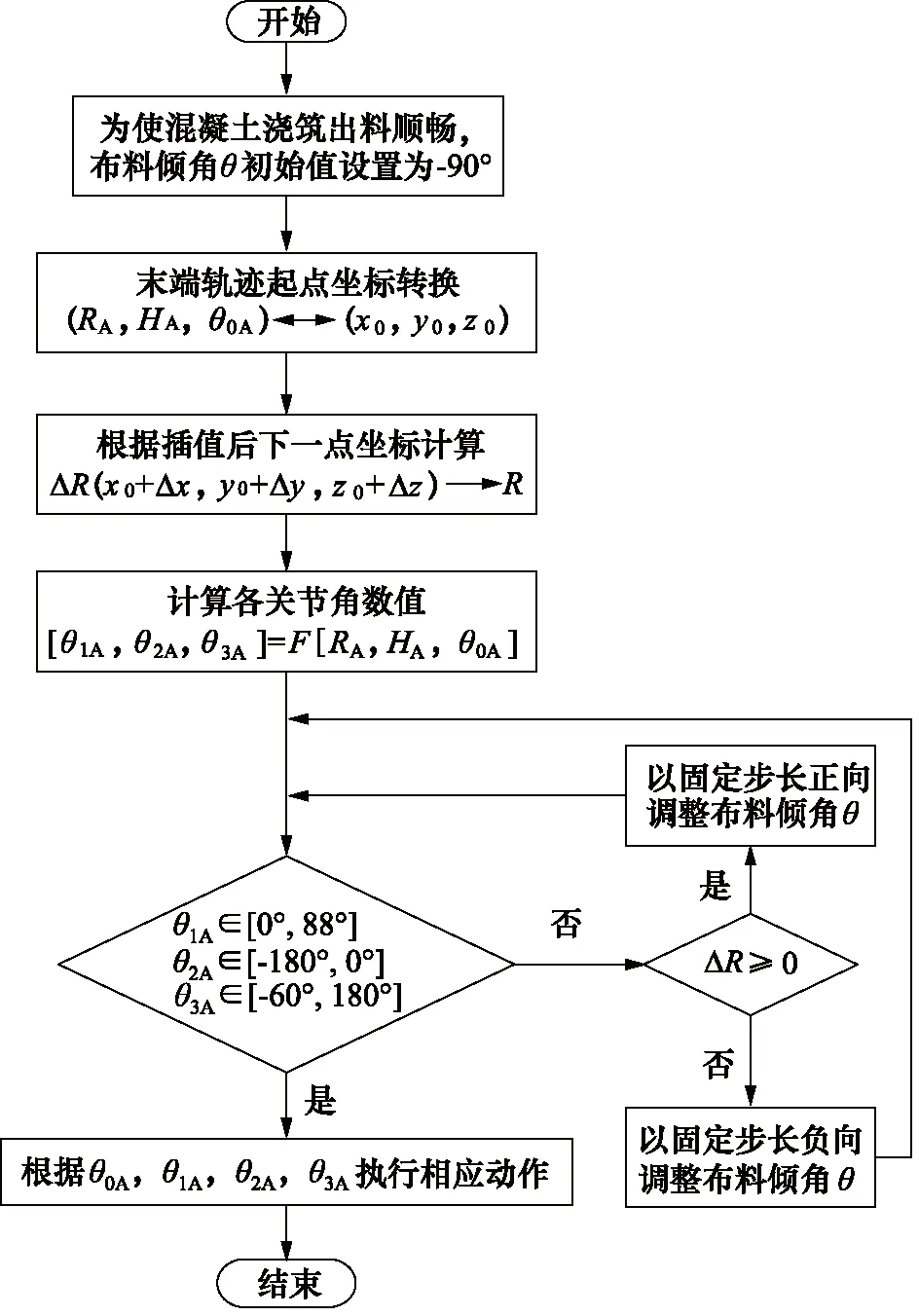
图4 基于姿态枚举算法末端轨迹控制程序流程图
2.2 姿态枚举算法的参数选取
应用姿态枚举算法对多自由度混凝土布料机械臂进行轨迹控制的过程中,对预设路径产生影响的参数,包括离散点个数n、初始布料倾角θ及倾角枚举步长Δθ。其中,初始布料倾角θ对预设路径的精度以及平滑性影响较小。
现以表1所述布料机械臂为对象,设置3组不同的参数如表2所示,采用基于姿态枚举算法的控制策略对轨迹进行控制,得到3#臂关节角θ3的变化曲线如图5所示。其中,设置初始倾角θ=-90°,起始点坐标:R=7000,H=0,θ0=0°,终点坐标:R=127000,H=0,θ0=30°。
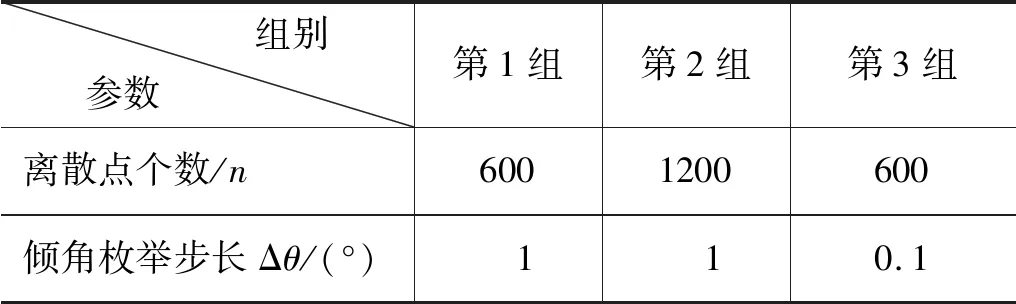
表2 基于姿态枚举算法的轨迹控制参数
分析图5可得,在该条件下,当倾角枚举步长保持在1°时,通过逆解模型求得的3#臂关节角波动在5°以上,且增加离散点个数对于预设轨迹的平滑性改善并不明显;当倾角枚举步长设为0.1°时,关节角波动减少至2°左右,预设轨迹的平滑性和稳定性大大改善。因此,在倾角传感器分辨率足够的情况下,采用姿态枚举算法对布料机械臂轨迹进行控制时,应尽可能减小倾角枚举步长Δθ的设置。
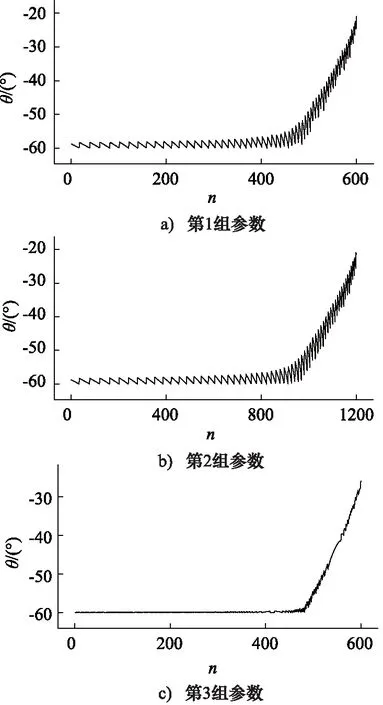
图5 不同参数下3#臂关节角变化曲线图
3 基于姿态枚举算法的混凝土布料机械臂轨迹控制联合仿真
3.1 AMESim-MATLAB-ADAMS联合仿真模型
为了验证基于姿态枚举算法的混凝土布料机械臂轨迹控制方法在实际工程应用中的可行性,以表1所述某13m-3Z型混凝土布料机械臂为对象,建立了基于AMESim-MATLAB-ADAMS的混凝土布料机械臂联合仿真模型。
通过在AMESim中建立阀控缸模型,在ADAMS中建立布料机械臂机械结构模型,在MATLAB/Simulink环境下建立机械臂控制模型并将三者结合进行联合仿真的方式,使仿真模型更加贴合实际。该联合仿真模型以MATLAB/Simulink为主体,并添加了AMESim与ADAMS的联仿接口。各个模块以及模块间的信息传递路径如图6所示。

图6 联合仿真模型各模块及信息传递路径
其中,轨迹的控制基于插值法进行,实时轨迹控制模块在每个仿真步中读取ADAMS模块经运动学求解得到的关节角度值。在控制精度允许的范围内,当关节角度达到目标位置时,应用基于姿态枚举算法的轨迹控制方法,实时地更新各关节目标角度,以供控制信号产生模块计算阀控信号值。
3.2 联合仿真结果及分析
首先,以本研究所提出的姿态枚举算法作为轨迹控制策略对一弧形目标轨迹进行仿真,其中的主要参数设置如表3所示。
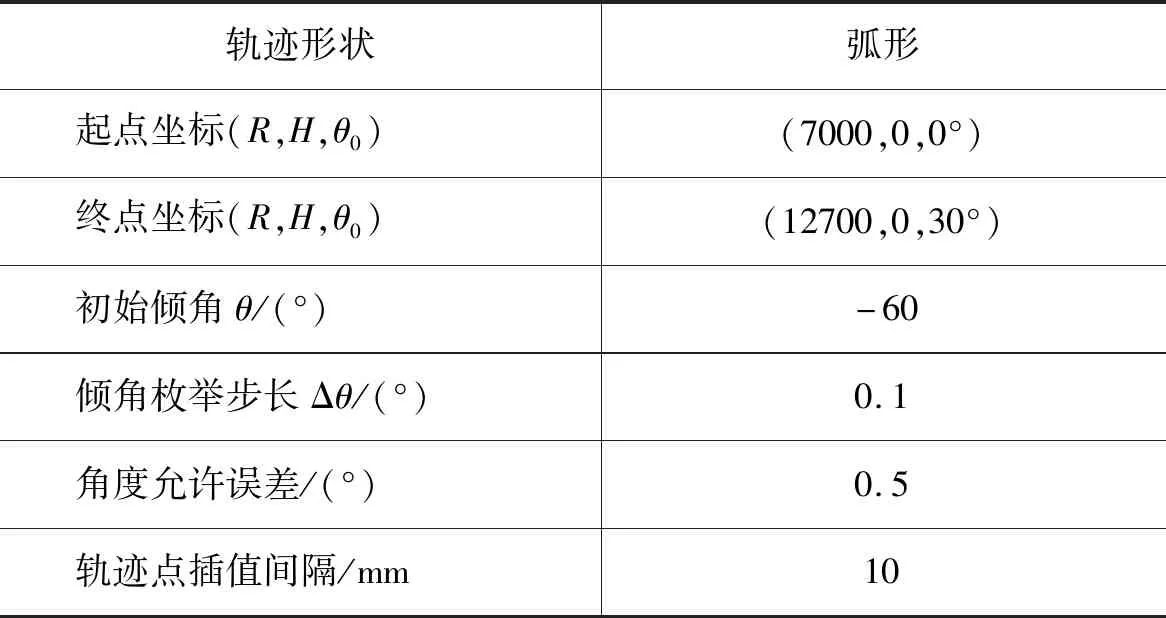
表3 基于姿态枚举算法的联合仿真主要参数设置
其次,对于具有多自由度的机械臂轨迹控制而言,遍历算法是一种简单且通用的控制算法。该算法和枚举算法具有相似性,两者均按一定步长对机械臂逆运动学进行求解结果的搜索,并依据附加的限定条件从结果解集中筛选出最优解。本研究以遍历算法作为轨迹控制策略进行仿真对比,布料倾角θ的遍历范围设置为[-70°,-1°],遍历步长设置为0.1°,初始倾角设置为-60°,最优解约束条件设置为各关节角变化量之和最小。得到2种不同控制策略下的末端轨迹曲线如图7所示,布料倾角随布料半径变化曲线如图8所示。

图7 末端轨迹曲线对比
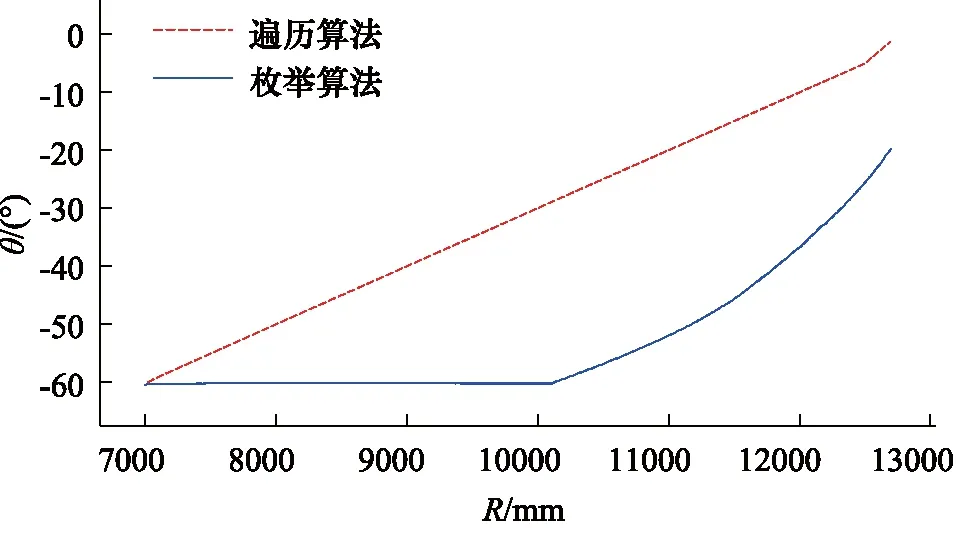
图8 布料倾角变化曲线图对比
从图7可以看出,在布料机械臂运动学逆解模型的基础上,2种不同的控制策略均能实现布料机械臂按照预定目标路线运动。
从图8可以看出,当采用基于遍历算法的轨迹控制策略时,布料倾角θ随布料半径增加而增加,最小值为-60.14°,最大值为-1.33°,倾角变化量为58.81°。当采用基于枚举算法的轨迹控制策略时,在布料半径为7000~10100 mm的运动段里,布料倾角最小值为-60.50°,最大值为-60.19°,波动仅为0.31°,基本稳定在-60°左右,证明在该运动段内软管-3#臂铰点与3# 臂一起以近似平移的方式移动;在布料半径大于10100 mm的运动段里,由于臂架伸展距离较远,布料倾角不能保持在-60°,并随布料半径增加而增加;但得益于姿态枚举的控制策略,从起点运行到终点的过程中,布料倾角最大值为-19.83°,倾角变化量为40.67°,与基于遍历算法的控制策略相比,变化量减少了30.8%。结果表明,尽管采用以各关节角变化量之和最小作限制条件的遍历算法有利于缩短油缸行程,减少能耗,但与混凝土出料口直接相关的3#臂摆动幅度较大。本研究提出的基于姿态枚举算法的混凝土布料机械臂轨迹控制方法限制了3#臂的摆动,减少了末端软管的径向甩动,增加了混凝土出料的稳定性。
4 结论
本研究以13m-3Z型混凝土布料机械臂为例,建立了该机械臂的运动学正、逆解模型,提出了基于姿态枚举算法的轨迹控制方法,分析了该方法不同参数对控制结果的影响规律,搭建了联合仿真模型,对比分析姿态枚举算法和遍历算法的仿真结果,得到以下结论:
(1) 倾角变化量反映布料机最后一节臂与水平面间夹角的波动情况。倾角变化量越小,则波动越小,末端软管随最后一节臂摆动的幅度越小,混凝土出料落点的控制精度越高;
(2) 与遍历算法相比,采用本研究提出的姿态枚举算法,可使布料倾角变化量减少30.8%。证明该算法可减少末端布料软管相对最后一节臂的转动,从而降低末端布料软管的径向甩动;
(3) 选取姿态枚举算法的参数时,减小倾角枚举步长Δθ可改善轨迹控制的平滑性和稳定性。

