基于SolidWorks调节阀Kv值数字化建模预测分析
王楚辉,凌 飞,孙 建,盛叶飞,吕 溢
(1.浙江三方控制阀股份有限公司,浙江 杭州 310000;2.浙江三方控制阀研究院,浙江 杭州 310000)
引言
调节阀作为一种节流机构,主要对流体流量、压力、流向等进行调控,通过阀芯、阀座改变流道的截面积,形成局部阻力,从而改变流体的压力和速度,达到调控效果,流体流过节流孔时压力和速度变化如图1所示[1]。流体在流过调节阀时,由于流阻问题,产生能量损失,通常用阀前后的压差来表示阻力损失的大小。要使调节阀能起到调节作用,就必须使阀前后有一定的压差。
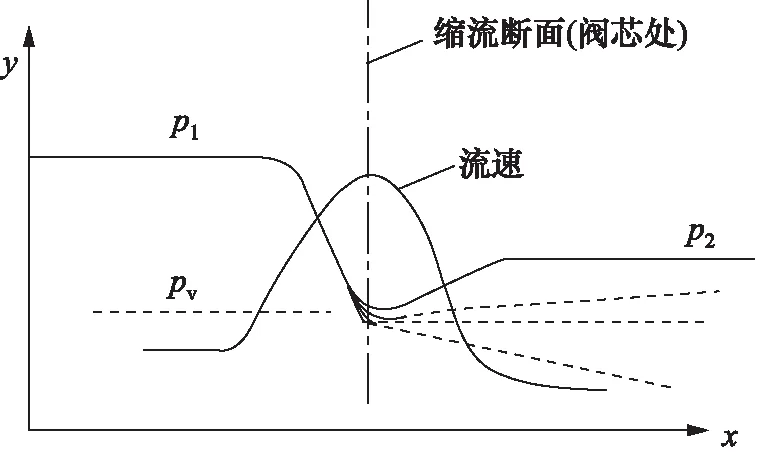
图1 流体流过节流孔时压力和速度的变化[1]
阀门在启闭和工作状态时,通过阀门的流体流场会改变并形成涡流,流场的变化是引起阀门振动和噪声的主要因素,对阀门流体流动特性的研究尤显重要。国内外学者对阀门进行了大量研究,屈铎等[2]通过有限元手段对球体内部流场进行了仿真分析,研究了阀腔结构对流体流动的影响,得出了阀内涡流形成的特点,为阀门流道设计及优化提供了理论依据;刘兆领等[3]基于PumpLinx进行某型齿轮泵的内流场特性模拟仿真,并将仿真结果与试验数据进行对比分析,验证了采用的仿真技术能够有效实现该型泵的特性分析;王阳阳[4]基于Fluent仿真软件,对安全阀启、闭全过程进行自适应动网格瞬态分析,结果表明,仿真分析可以观测到开启瞬间阀芯的回弹趋势,还能提供安全阀内部流场信息,是研究瞬态流场的有效手段;张玉祥等[5]应用k-ε标准湍流模型,模拟分析了球阀在不同阀芯开度下的阀门内部流场,得出阀门开度较小时,阀门内部会产生较大速度梯度和压力梯度,当阀门开度逐渐增大时,节流效应减弱,阀门下游压力变化减小,漩涡减小直至消失;刘兆领等[6]针对内缩型平衡阀的噪声问题,建立了内部流场的数学模型,利用Fluent仿真软件进行了液气两相流仿真,研究了流道壁面的噪声分布情况;张宏等[7]针对大流量多路阀稳态液动力问题,对阀芯受力情况进行了数值模拟仿真,通过对比不同湍流模型对仿真结果的影响,得出Realizablek-ε模型在大流量多路阀稳态液动力仿真中能够更好的拟合试验数据;任恒等[8]通过L9(34)正交试验与数值模拟相结合的方法对比例减压阀进行了优化设计,有效改善了比例减压阀的动态特性;金伟等[9]针对旋转阀的工作原理及其在工作过程中阀体内部流体流动特性,利用 Fluent 软件对旋转阀进行流场分析,得到了流体在旋转阀中的运动规律及流体压差变化情况;SRIKANTH C等[10]应用CFD流动网格技术对阀门内流体流动情况进行了仿真研究;MORITA R等[11]应用CFD技术对蒸汽调节阀内部流体流动情况进行了仿真研究,分析了引起阀门振动的因素,并进行了试验验证。本研究针对调节阀流量特性,应用SolidWorks 软件对阀内流体流动进行模拟分析,提取流体通过阀门的流量及压差,求得其Kv值,并在相同条件下进行流量试验,通过试验对比验证仿真结果的可靠性,为应用CFD技术研究阀门内部流体流动问题提供了理论参考。
1 SolidWorks 数字化建模
调节阀调节过程就是阀前、后形成压差的过程,进而达到改变流体的通过能力。应用SolidWorks软件模拟流体在调节阀内的流动过程,提取仿真数据,构建流体力学数字化模型,为调节阀调控机理的研究提供理论参考。
1.1 几何模型建立
应用SolidWorks软件构建调节阀三维模型,并在CFD模块中进行仿真分析。调节阀的内件(阀座/套筒、阀芯)是保证调节能力的核心部件,在建模时要保证其尺寸的准确性并保证装配关系。本研究只研究调节阀的Kv值,在构建调节阀三维模型时可以进行简化,只保留与介质接触的主要部件;同时根据调节阀流量测试试验标准,在调节阀入口、出口处分别加装长度为2倍、6倍管径(2D,6D)的管道,避免流体在阀体内发生扰动对试验结果产生影响。调节阀模型如图2所示,图2a为调节阀三维模型,图2b为调节阀三维简化模型,图2c为加装管道后调节阀简化模型。
1.2 流体数学模型
在研究流体流动问题时,都会引入一系列控制方程,通过构建流体数学模型进行求解,常用到的有连续性方程、动量方程等。流体运动的控制方程根据质量守恒、动量守恒和能量守恒得出。试验研究介质为不可压缩流体,且流体的黏度系数和热传导数为定值,因此得到如下流体控制方程[12]:
连续性方程:
V=0
(1)
动量方程:

(2)
式中,ρ——流体密度,g·cm-3
V——流体速度矢量
F——体积力
标准k-ε湍流模型[13],湍动能k方程:
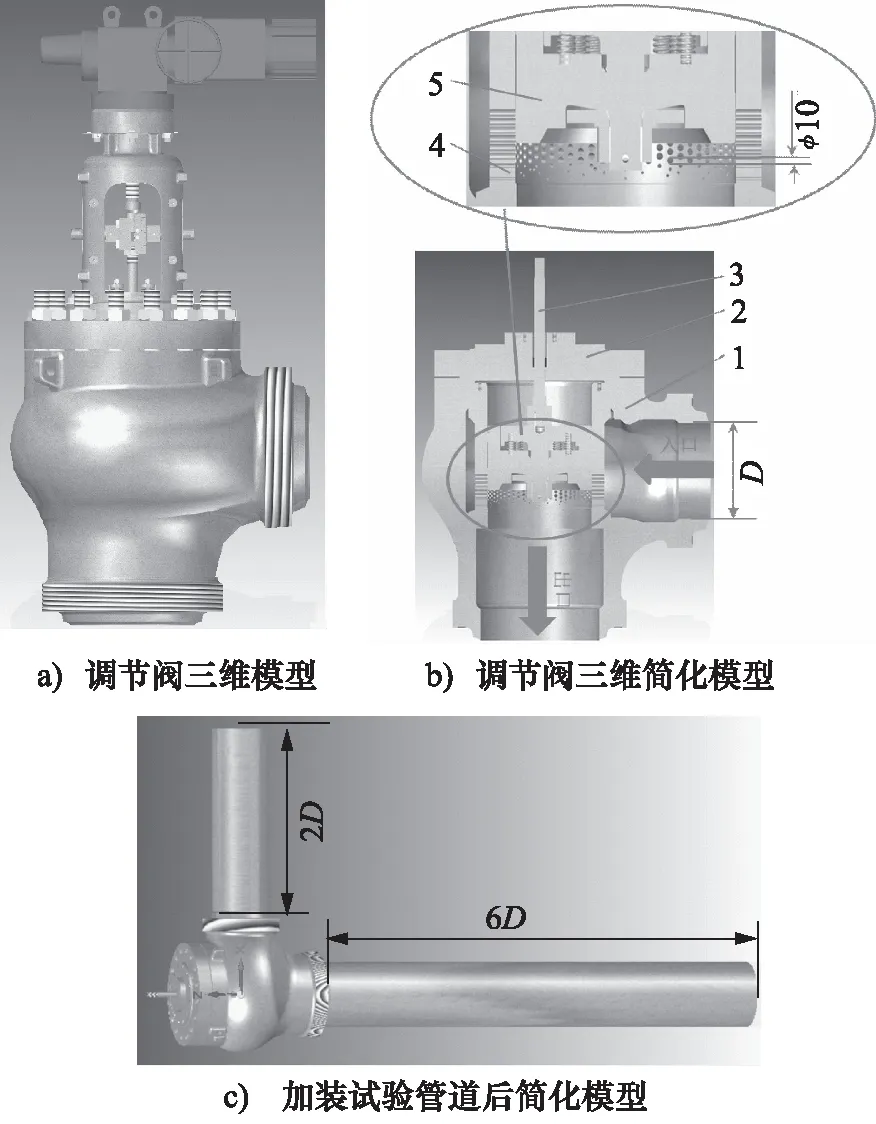
1.阀体 2.阀盖 3.阀杆 4.套筒 5.阀芯图2 调节阀模型
(3)
耗散率ε方程:
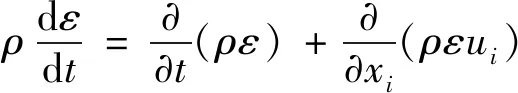
(4)
式中,xi,xj——坐标分量
ui——速度分量
Ym——湍流脉动膨胀对耗散率影响
μ——分子黏度
C1ε,C2g,C3g——常数
μ1——湍流系数
σε,σk——湍流普朗特数
Gk——速度引起的湍动能
Sk,Sε——源项
Gb——浮力引起的湍动能
通过对以上控制方程进行离散变换,得出其数学模型,将模型图分解成无数个小网格(微元化处理),将研究问题的初始条件和边界条件代入,求得方程的解。该求解过程可以通过CFD技术,在仿真软件中完成,直接得到仿真结果。
1.3 边界条件设置
本试验研究流体的流动问题,对其Kv值进行求解,而Kv值又是流量与压差的函数;只需确定流体流量或压差,即可对研究的流体流动问题进行求解。试验只讨论了边界以内的流体流动问题,设置了静态压力边界条件。
流体Kv值计算过程:
对于不可压缩流体,当流体流过阀门时,会产生能量损失;对于不可压缩流体,根据能量守恒可得:
H=(p1-p2)/ρg
(5)
当阀门开度不变时,流经阀门流体的能量损失与流体动能成正比:
H=Cdw2/2g
(6)
w=Q/A
(7)
式中,H——能量损失
p1,p2——阀前、后压力,kPa
g——重力加速度
w——平均流速
Q——体积流量,m3/h
A——阀流道横截面积,cm2
Cd——阀阻力系数
将单位带入式(5)~式(7)中,计算后得:
(8)
令:
(9)
将式(9)中的密度ρ单位化成kg/m3,阀门压力p1,p2单位转化成MPa,即可得:
(10)
式中,ρ——介质密度,kg/m3
1.4 网格划分
工件网格划分质量对仿真结果有着重要影响,网格划分的疏密度既要考虑仿真的精度,又要考虑模拟的时间,结合实际,确定合适的网格尺寸[14]。针对流体分析,在流道截面上的网格数量不少于3层,通常将网格最小单元尺寸设为流道最小截面尺寸的1/3,并调控网格的最大、最小单元尺寸比例,给定网格自适应划分的标准。图3为调节阀截面网格模型,其最小流道截面尺寸为 10 mm,最大流道截面尺寸为 350 mm,故最小网格单元尺寸设为3 mm,网格的最大、最小单元尺寸比例设为 7,比例过大会引起仿真失真、不收敛,通常比例不大于12。
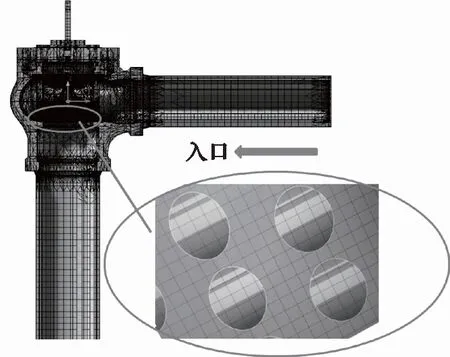
图3 调节阀截面网格模型
2 调节阀Kv值预测分析及试验对比
CFD技术的应用,使流体流动问题的研究进入了数字化、可视化阶段,极大降低了研究成本,节约了研究时间。本研究基于SolidWorks软件,对调节阀的流量特性进行仿真分析,求解其在不同开度时的仿真Kv值,得出其理论流量特性曲线;再在同等条件下进行流量试验,检测对应开度时的流量,计算得出试验Kv值,并与仿真结果进行对比分析,验证仿真结果的可靠性。
2.1 调节阀Kv值预测分析
本研究的调节阀基本参数:DN350,PN160,最大调节行程100 mm。应用 SolidWorks 软件完成调节阀三维简化模型构建后,直接进入流体仿真模块(flow simulation)。流体介质设为水(常温),管道摩擦因数0.3,管道壁面设为绝热,介质自重影响忽略。根据1.3节完成初始条件设置并划分网格。载荷参数设置见表1。

表1 仿真载荷参数设置
将载荷数值带入到仿真模型中进行求解运算,提取仿真数据进行分析。图4为流体在阀门内流动速度云图。

图4 流体在阀门内流速云图
从图4中可以看出,流体在进入阀腔前的加装管道内流速稳定,在进入阀腔后流速出现较大波动,这是因为阀芯与套筒改变了流道的截面积,使流体流动遇阻,流体在通过阀芯时出现压力变动,引起流速改变。当流体离开阀腔后,流速开始缓慢恢复稳定,这是因为流体离开阀腔后,压力开始恢复直至稳定,流速亦趋于稳定。图4中流体在距离阀腔后约2.5倍管径管道处,流速基本稳定,4.5倍处流速完全稳定,因此,在调节阀入口、出口处分别加装长度为2倍、6倍管径的管道,可以有效避免流体在阀体内发生扰动,对仿真结果产生影响。
图5为阀芯100%开度时流体质量流量M,图6为阀芯100%开度时阀门出、入口压力。
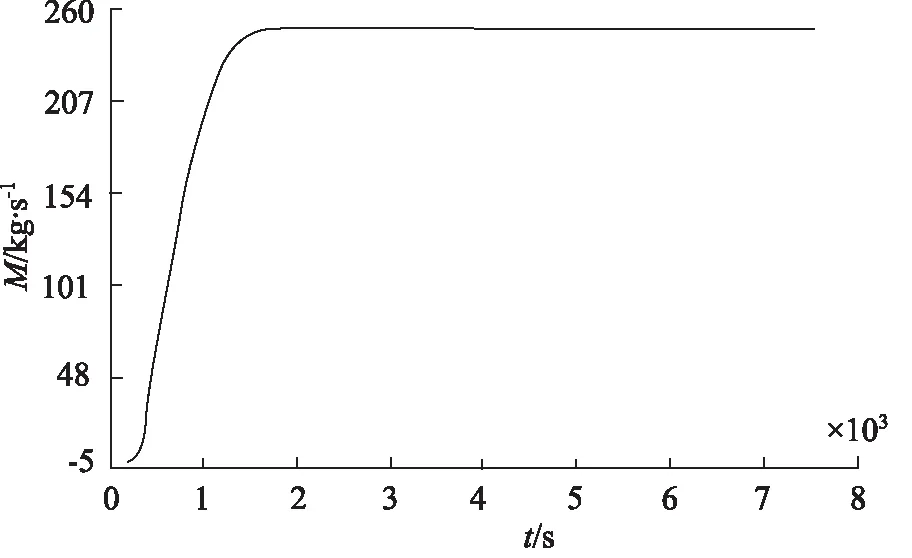
图5 阀芯 100%开度时流体质量流量

图6 阀芯 100%开度时管道出、入口压力
由图5可以看出,在流体流动稳定后,流体通过阀门的质量流量保持稳定,符合调节阀的调控功能要求;图6可以看出,在仿真的全过程中,管道取压口处压力稳定不变,保证了仿真数据的可靠性。
根据以上仿真方法,建模求解出所有开度的流体质量流量,并将仿真数据带入式(10)求得Kv值。阀芯不同开度时的质量流量与Kv仿真值见表2。
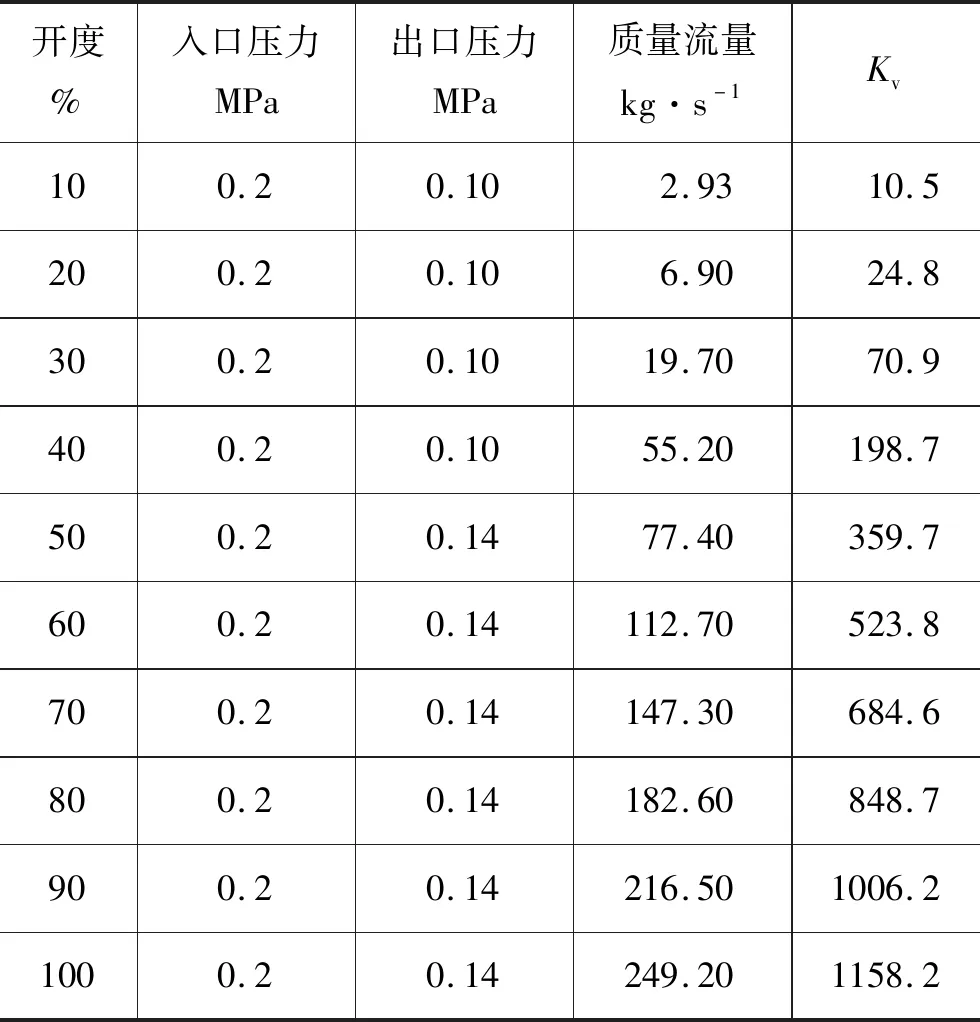
表2 阀芯不同开度时的质量流量与Kv仿真值
2.2 调节阀 Kv值试验检测及对比分析
通过CFD技术仿真得到的数据,还处于理论阶段,为验证仿真数据的可靠性和实用性,在相同条件下(流体介质、边界条件、载荷条件等),对以上调节阀进行流量测量试验,得到不同阀芯开度时的流量和压差值。图7为流量试验系统简图,通过“上/下游节流阀”控制流入“试验样品阀”的介质流量[15]。

图7 流量试验系统[15]
图8a为调节阀流量试验实物,图8b为阀门流量测量系统。通过该系统可以将试验过程中的流量与压强实时显示出来,便于条件控制和数据提取。

图8 阀门流量试验
将试验测得的流量与压差带入式(10)求出Kv试验值,并与仿真值进行对比。图9为Kv试验值与仿真值对比曲线。

图9 Kv试验/仿真值曲线
从图9可以看出,当阀门开度较小时(不大于30%),Kv试验与仿真偏差较大,且开度越小偏差越大,这是因为较小开度时通过阀门的流量较小,在相同偏差量情况下,流量基数越小,偏差的百分比就越大;当阀门开度较大时(大于30%),试验与仿真比较吻合,偏差值小于5%。调节阀在实际应用过程中,其实际应用阀门开度在40%~80%之间。因此,通过CFD技术仿真得到的阀门Kv值曲线,可以作为阀门设计时的理论参考,这将极大提高了设计效率和经济效益。
3 结论
Kv值作为调节阀设计和应用的主要参数,是判定调节阀是否合格的重要指标。本研究应用SolidWorks软件对调节阀进行数字化建模,完成了调节阀流量仿真分析,得到了阀门不同开度时的Kv值。通过将仿真与试验进行对比分析,得出在阀门开度大于30%时,试验与仿真偏差值皆小于5%,验证了仿真数据的可靠性。为应用CFD技术进行阀门流量研究提供了理论参考,对提高阀门设计效率具有指导意义。

