不确定失效阈值影响下考虑设备剩余寿命预测信息的最优替换策略*
王泽洲,陈云翔,蔡忠义,王莉莉,项华春
(1.空军工程大学 装备管理与无人机工程学院,陕西 西安 710051;2.中国人民解放军93920部队,陕西 汉中 723200)
随着科技的进步,航空、航天、核能等诸多高新技术领域得到快速发展,同时也对相关装备提出了更高的安全性要求。为了切实提升装备的可靠性,减少系统运营维护费用,预测与健康管理(Prognostics and Health Management,PHM)技术应运而生,并取得了良好效益[1-3]。PHM技术的核心是通过监测系统关键组成设备的性能退化数据来预测其剩余使用寿命,并提出相应的维修保障策略,从而提升装备运行的安全性与可靠性,降低故障或失效带来的风险。
传统的维修决策研究多基于随机过程描述设备的退化规律,进而依据设备的可靠性指标进行维修策略优化。Kallen等[4]采用Gamma过程描述设备的退化过程,并分析了检测周期与预防性维修阈值对失效风险和费用的影响。van der Weide等[5]通过几何过程预测设备的退化趋势,并优化了设备的维修时间。Ho等[6]则基于Markov过程构建设备性能退化状态转移方程,并以费用为目标函数建立优化模型,从而确定最优检测时间和维修时间。然而,上述研究对设备实际退化过程的描述并不完善,均是基于经验公式构建退化模型,而未能充分利用设备运行过程中的状态监测数据来进行退化建模,这将导致所建模型难以准确反映设备的真实退化规律,进而影响维修决策结果的科学性与合理性。
针对传统维修决策方法存在的不足,利用状态监测数据准确构建设备退化模型,并基于设备剩余寿命预测信息进行维修决策的方法开始逐步得到研究者的关注[7-9]。Guo等[7]通过引入残余退化量描述维修活动对设备退化量的影响,并推导出对应的剩余寿命函数,进而通过建立优化模型确定最优预防性维护阈值。Zhang等[8]通过引入改善因子描述维修活动对设备退化速率的影响,并以退化速率为对象分析了设备的最优维修策略。然而,文献[7]和文献[8]仅单独研究了退化速率或退化量对维修决策的影响,未能分析二者对维修决策的综合作用。为了进一步提升维修决策的科学性,裴洪等[9]在综合考虑维修活动对退化速率和退化量影响的基础上,基于设备的剩余寿命预测信息,构建了维修决策模型,从而确定了最优检测时间和预防性维护阈值,降低了设备的寿命周期费用。然而,文献[9]所提维修决策方法仅适用于可修复设备,难以满足不可修复设备制定最优维修策略的需求;且该方法在剩余寿命预测过程中认为设备性能退化失效阈值满足固定值假设,忽略了不确定失效阈值对剩余寿命预测的影响,这可能降低剩余寿命预测的准确性[10-12],进而对制定科学合理的维修策略产生消极影响。此外,目前针对不确定失效阈值分布系数确定方法的研究尚不充分,文献[13]提出采用极大似然估计(Maximum Likelihood Estimation,MLE)对不确定失效阈值的分布系数进行估算,然而该方法在似然函数不存在解析形式时,仅能通过泰勒级数展开得到近似解,降低了参数估计的准确性,也对设备最优维修决策造成了不利影响。
针对上述问题,本文以不可修复设备为研究对象,开展了基于剩余寿命预测数据与不确定失效阈值的设备最优替换策略研究,主要创新点有:
1)基于期望最大(Expectation Maximization,EM)算法提出一种新型不确定失效阈值分布系数估计法,相较于传统MLE方法,能有效提升参数估计的准确性;
2)基于设备的剩余寿命预测数据,依据更新报酬理论建立维修决策模型,分析不确定失效阈值对最优替换时机的影响。
1 设备剩余寿命预测
1.1 退化建模
Wiener过程可以准确描述具有非单调退化特征设备的退化规律,且具备良好的数学特性,现已被广泛应用于退化建模研究[14]。
理想状态下,Wiener过程可表示为:
X(t)=X(0)+at+bB(t)
(1)
其中:X(t)表示设备在t时刻的性能退化量;a为漂移系数;b为扩散系数;B(t)表示标准布朗运动;X(0)表示初始时刻的性能退化量,通常认为X(0)=0。
在实际运行过程中,受设备内外部应力影响以及非理想测量手段制约,通常难以准确描述设备的退化过程。为了解决该问题,现有研究多通过将非线性、个体差异以及测量误差融入退化建模过程,形成改进的Wiener退化模型,其具体表达式如式(2)所示。
Y(t)=aγ(t,θ)+bB(t)+ε
(2)
1.2 参数估计
1.2.1 退化模型参数估计
(3)
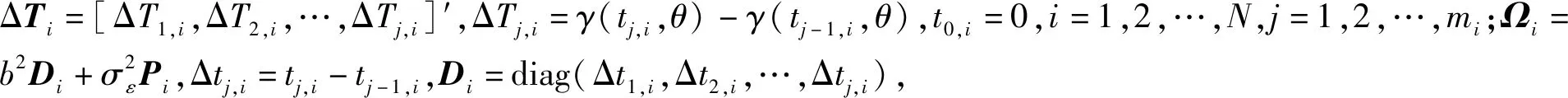
令Y=[ΔY1,ΔY2,…,ΔYN],则Y表示全部性能退化监测数据,其对数似然函数可表示为:
(4)
lnL(Y)=
(5)
(6)
(7)
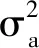
(8)
(9)
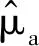
1.2.2 不确定失效阈值分布系数估计
在真实使用环境下,同类设备不同个体间往往存在差异性,这种个体差异在退化过程中多体现为设备退化速率(漂移系数a)的随机性,而在失效过程中则体现为失效阈值ω的不确定性。例如,弹簧的伸缩极限、铣刀的磨损上限、风机的振动阈值等,不同个体间失效阈值相似但不完全相等,难以采用一个固定值进行明确,因而多采用具有不确定性的区间值进行描述。为了科学分析失效阈值的不确定性,现有研究多采用随机变量来描述设备的不确定失效阈值,其中正态随机变量成了当前的研究热点[11-12]。
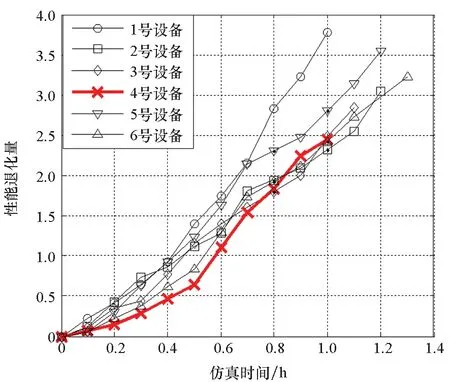
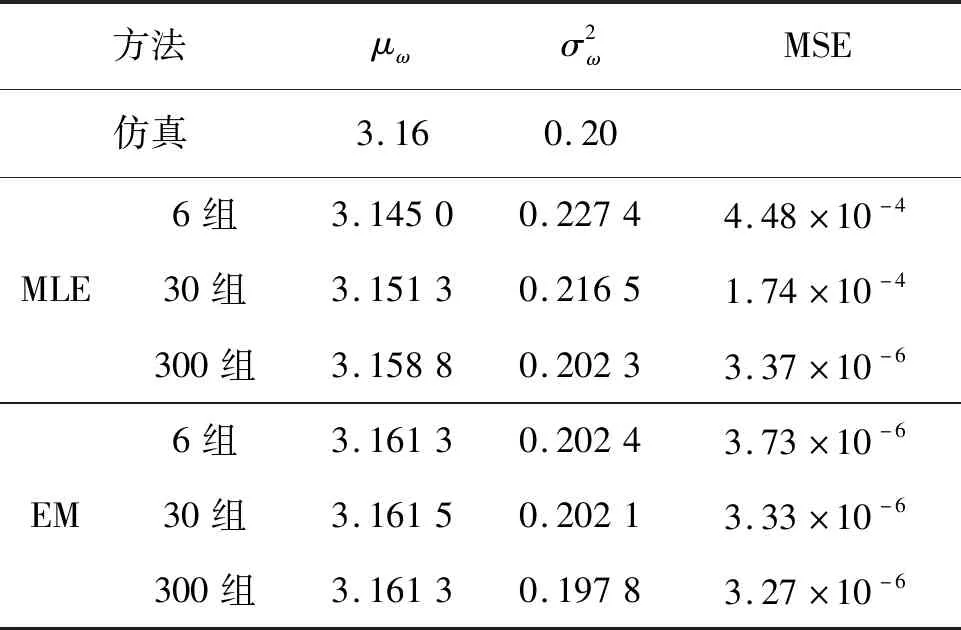
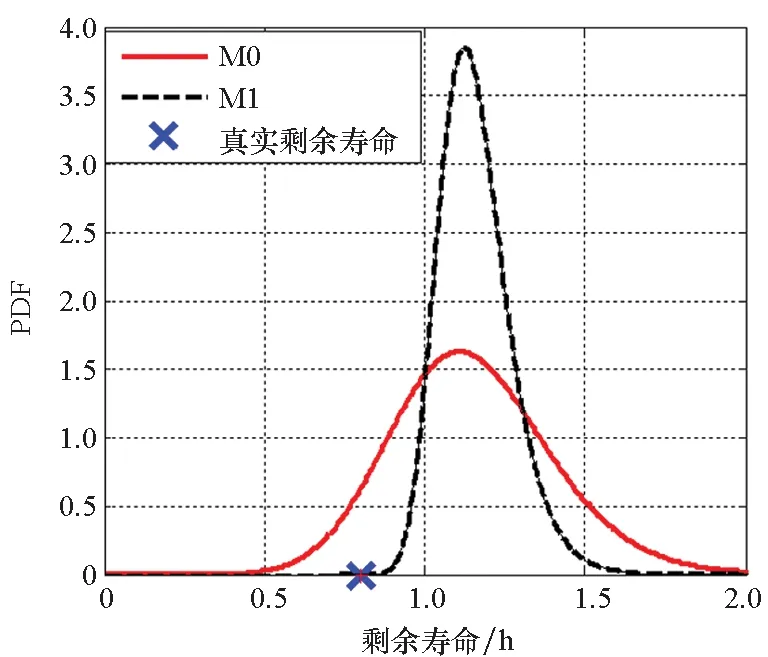
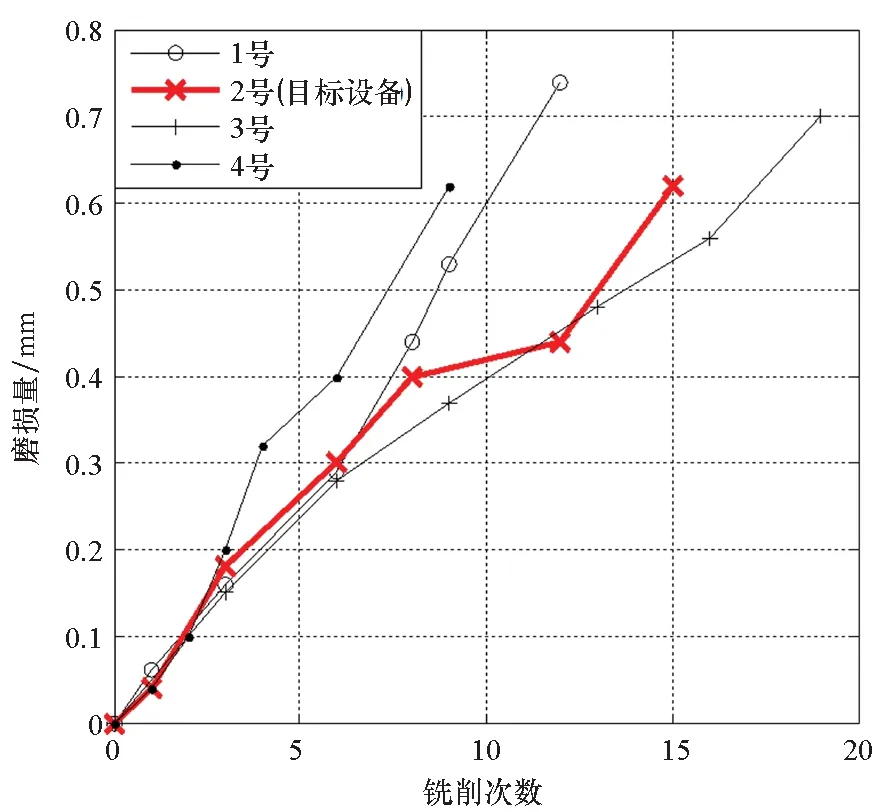
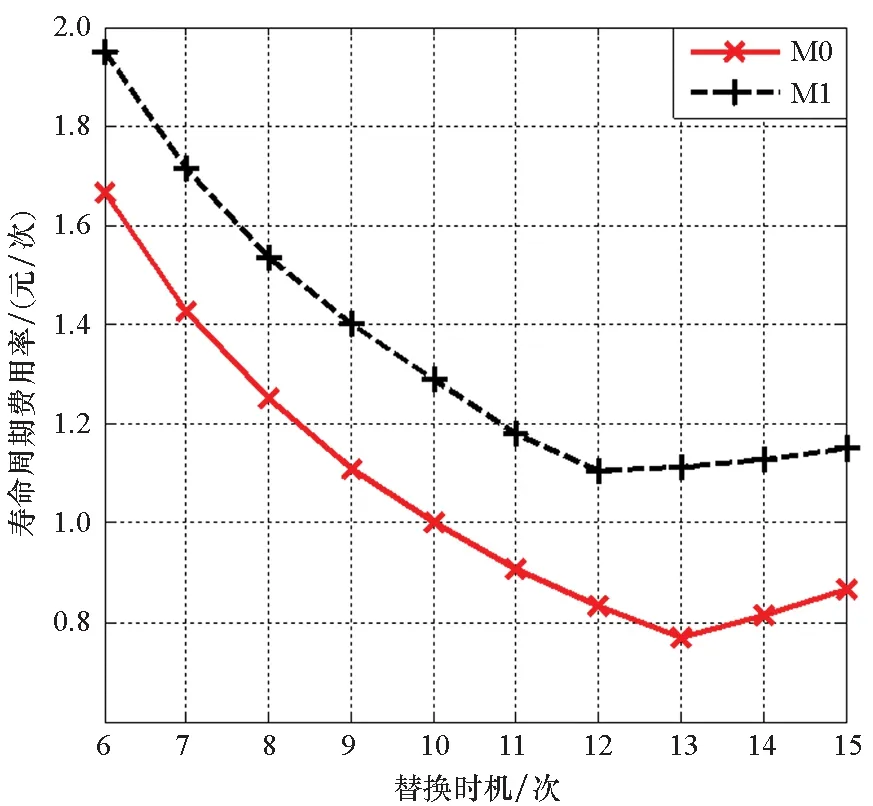
在设备的实际退化过程中,易知设备性能退化的失效阈值应大于设备失效前一时刻的性能退化量X(t*),0 f(ω)= (11) 其中:Φ(·)为标准正态分布的累积分布函数。 由于Φ(·)不存在解析表达式,难以采用传统MLE法来对其进行参数估计,为此,本文提出一种基于EM算法的不确定失效阈值分布系数估计方法。EM算法针对缺失/隐含数据情形下的参数估计具有良好效果,因此适用于估算截断正态分布的参数估计值。 E步:对式(12)求虚拟失效阈值ω′的期望,可得 (13) 由截断正态分布的性质可知,对于任意ω′i均满足: (14) (15) (16) (17) (18) 令式(17)、式(18)等于零,可得 (19) 由于R未知,因此还需计算E(R)。文献[15]给出了E(R)的计算方法,如式(21)所示。 (21) 将式(21)代入式(19)、式(20)即可得到M步的迭代公式: (22) 其中: (24) 设备的寿命通常被定义为性能退化量首次达到失效阈值的时间,也被称为首达时间(First Hitting Time,FHT)。基于上述定义,设备的寿命可表示为: T=inf{t:X(t)≥ω|X(0)<ω} (25) 对于式(2)所描述的退化模型,在不考虑测量误差ε的前提下,可证明其寿命T近似服从逆高斯分布,对应的概率分布如式(26)所示[14]。 (26) 进一步可推导出tk时刻设备剩余寿命lk概率分布如式(27)所示。具体证明过程详见文献[16]。 fLk|ω,X1:k(lk|ω,X1:k)≈ (27) 其中:xk表示tk时刻目标设备所对应的真实性能退化数据;X1:k则表示直至tk时刻所获取的全部真实性能退化数据; ψ(lk)=γ(tk+lk,θ)-γ(tk,θ) (28) (29) (30) 引理1的证明过程详见文献[16]。 则基于全概率公式,可得: fLk|ω,Y1:k(lk|ω,Y1:k)= P(X1:k|Y1:k)P(a|Y1:k)dxkda= Ea{Exk[fLk|ω,a,X1:k(lk|ω,a,X1:k)]} (31) 其中:Y1:k表示直至tk时刻所获取的全部性能退化数据监测值;P(·)为求概率。 令xk=D1,a=D2,E=β(lk),F=ψ(lk),G=b2lk,利用引理1,则可求出固定失效阈值条件下设备剩余寿命的PDF为: (32) 为了推导考虑不确定失效阈值条件下设备剩余寿命的PDF,本文给出如下定理1。 定理1若D~TN(μ,σ2),E,F∈R,G∈R+,则 (33) 定理1的证明过程可由文献[16]中引理1的证明经变形得到,这里不再进行单独推导。 基于全概率公式,若Y1:k已知,则考虑不确定失效阈值条件下设备的剩余寿命可表示为: fLk|Y1:k(lk|Y1:k) =Eω[fLk|ω,Y1:k(lk|ω,Y1:k)] (34) 若令ω=D,H4=E,H2=F,H1=G,将其代入式(33),可得设备剩余寿命的PDF为: fLk|Y1:k(lk|Y1:k)≈ (35) 其中: (36) H2=yk+μaψ(lk) (37) (38) (39) 基于上述分析,可得考虑不确定失效阈值条件下设备剩余寿命的累积分布函数为: (40) 基于更新报酬理论[17]建立决策模型,进而确定最优替换时间。具体决策模型可表示为: (41) 其中,C(τ)表示τ时刻进行替换操作对应的期望寿命周期费用率,EC表示设备运行寿命周期总费用的期望,ET表示设备运行总时间的期望。进一步分析可得: EC=c1P(t>τ-tk|Y1:k)+c2P(t<τ-tk|Y1:k) (42) (43) 其中:c1表示预防性替换的费用,c2表示失效性替换的费用,tk为设备当前运行时间,τ为替换时刻,f(l)为变量l的函数且l=τ-tk。 基于Wiener过程的性质,易知lk=τ-tk,则f(l)等价于第1.3小节中设备剩余寿命的概率密度函数fLk|Y1:k(lk|Y1:k),进一步分析可知P(t<τ-tk|Y1:k)等价于FLk|Y1:k(lk|Y1:k)。进而可将替换策略决策模型改写为: (44) 具体证明过程如下: EC=c1P(t>τ-tk|Y1:k)+c2P(t<τ-tk|Y1:k) =c1[1-P(t<τ-tk|Y1:k)]+c2P(t<τ-tk|Y1:k) =c1+(c2-c1)P(t<τ-tk|Y1:k) =c1+(c2-c1)FLk|Y1:k(l|Y1:k) (45) =tk+lk[1-FLk|Y1:k(lk|Y1:k)]+lkFLk|Y1:k(lk|Y1:k)- (46) 由式(45)除以式(46)即可证明式(44)。 通过求解式(44)即可得到设备的最优替换时机。 图1 仿真退化轨迹Fig.1 Simulation of degradation path (a) μω 为了验证前文所提基于EM算法的不确定失效阈值分布系数估计法较传统MLE方法更具优势,本文引入均方误差(Mean Squared Error,MSE)作为判别标准进行分析。MSE的定义式为: (47) 为了进一步消除仿真结果的随机性,在原有仿真参数的基础上,再分别仿真出30组、300组退化数据,对应得到30个、300个仿真退化失效阈值数据,并采用EM与MLE方法分别进行参数估计,得到参数估计结果如表1所示。 表1 不确定失效阈值分布参数估计Tab.1 Estimation of uncertain failure threshold distribution parameters 表1中MLE对应的失效阈值分布系数估计值由MATLAB软件中normfit命令求出。由表1可知,同等仿真数据量条件下,EM算法对应的参数估计值较MLE方法更贴近于实际仿真参数,且MSE值更小,表明EM算法具有更高的估计准确性。进一步分析可以发现,MLE方法对仿真数据量较为敏感,随着仿真数据量的增多,MLE方法的参数估计值逐步接近于真实值,且对应MSE值逐步减小;而EM算法对仿真数据量变化的稳定性更好,随着仿真数据的增多,EM算法估计结果波动较小,参数估计误差变化不明显。基于上述分析可以证明,在中、小样本条件下,EM算法的准确性要明显优于传统的MLE方法。而在工程实际中,退化数据往往具有小样本特性,进一步说明了EM算法具有较高的工程应用价值。 为了进一步分析失效阈值的不确定性对设备剩余寿命预测与维修决策的影响,选取4号设备为目标设备进行研究(目标设备寿命为1 h,失效阈值为2.45)。为便于描述,记考虑不确定失效阈值的最优替换策略模型为M0,考虑固定失效阈值的最优替换策略模型为M1。则针对M0与M1模型,不同状态监测时刻(0.2 h、0.4 h、0.6 h、0.8 h)对应剩余寿命预测情况如图3所示。 (a) tk=0.2 h 由图3可知,在不同状态监测时刻,M0对应的剩余寿命PDF均可以包含设备的真实剩余寿命,而M1对应的PDF均无法包含设备的真实剩余寿命,表明M0较M1的剩余寿命预测准确性更高,体现了在剩余寿命预测过程中考虑不确定失效阈值的必要性。若假设c1=55元、c2=95元,结合上述分析得到的剩余寿命预测数据,将其代入式(44),即可确定最优替换时机,具体结果如图4所示。 图4 M0、M1对应的最优替换策略Fig.4 Optimal replacement strategy under M0 and M1 由图4可知,M1模型的最优替换时机为τ=0.7 h,对应的最小期望寿命周期费用率为8.538元/h;M0模型的最优替换时机为τ=0.8 h,对应的最小期望寿命周期费用率为7.655元/h。由此可以说明,在确定设备最优替换策略的过程中,考虑不确定失效阈值将有助于延长设备的运行时间,减少维修保障的费用消耗。 基于NASA公开数据源中的铣刀退化数据进行分析(如图5所示)[18]。铣刀是典型的不可修复组件,当铣刀的磨损量超过一定阈值时,铣刀发生失效。为避免铣刀失效造成的产品不合格问题与生产安全问题,需要实时监测其退化状态,并适时采取更换策略,确保生产的安全性与经济性。 图5 铣刀退化数据Fig.5 Milling degradation data 假设铣刀预防性替换费用为c1=10元,失效性替换费用为c2=100元,且当前目标铣刀已完成了5次铣削操作。基于本文第2节建立的最优维修决策模型,可得目标铣刀的最优替换时机,详见图6。 图6 铣刀最优替换策略Fig.6 Optimal replacement strategy of milling 由图6可知:M0求解得到的铣刀最优替换时机为第13次,对应寿命周期费用率为0.769 2元/次;而M1得到的铣刀最优替换时机为第12次,对应寿命周期费用率为1.106 3元/次。由此可知,本文所提最优维修决策方法能够延长铣刀的可靠使用寿命并降低其寿命周期费用消耗。该结论与仿真结果相一致,进一步说明了本文所提方法的优越性。 通过研究,建立了基于剩余寿命预测数据与不确定失效阈值的维修决策优化模型,确定了不可维修设备的最优替换时机。主要结论有: 1)设备失效阈值的不确定性真实存在,在设备剩余寿命预测研究中考虑不确定失效阈值具有合理性,能够有效提升设备剩余寿命预测的准确性。 2)针对不确定失效阈值分布系数的估计问题,EM算法较MLE算法在中、小样本条件下适用性更强且准确性更高,更能满足工程应用要求。 3)基于剩余寿命预测数据与不确定失效阈值的维修决策模型可以实现设备的最优替换策略。同不考虑不确定失效阈值的决策结果相比,考虑不确定失效阈值的可靠使用寿命显著延长,设备寿命周期费用率明显降低。 在研究中,不确定失效阈值分布下限值κ多基于工程经验人为给定,这可能引入主观误差,不利于实现科学决策。因此,未来应着重针对κ的估计方法展开研究,以进一步提升维修决策的准确性。
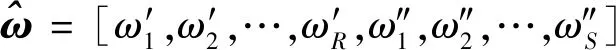
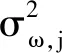


1.3 剩余寿命分布推导
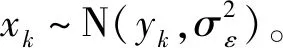
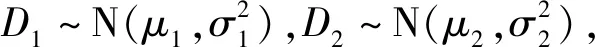

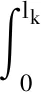
2 最优替换策略决策模型
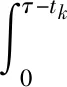
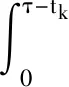
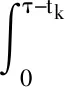
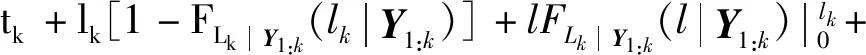
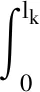
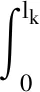
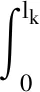
3 算例分析
3.1 仿真退化数据分析
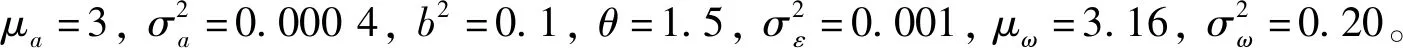
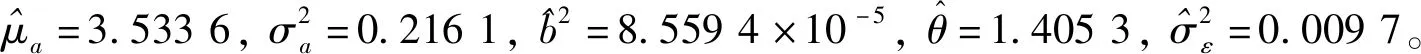
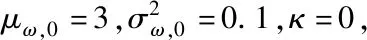
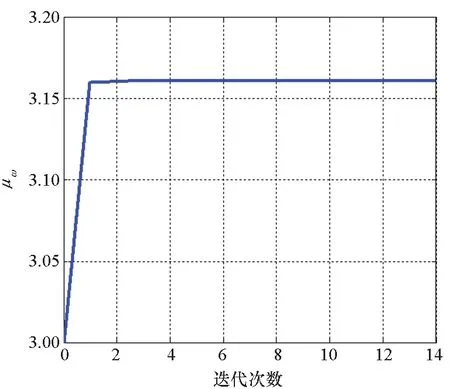
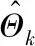

3.2 真实退化数据分析
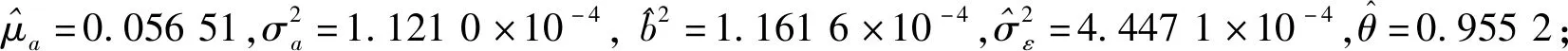
4 结论

