基于序列径向基函数的运载火箭蒙皮桁条结构轻质优化*

王志祥，欧阳兴，王 斌，张大鹏，雷勇军

(1.国防科技大学 空天科学学院，湖南 长沙 410073；2.北京宇航系统工程研究所，北京 100076)

薄壁加筋圆柱壳在飞行器结构中得到了广泛的应用，现有的运载火箭型号有80%的箭体舱段采用整体加筋和桁条加强的薄壁壳体结构，如运载火箭的级间段蒙皮桁条和贮箱等结构[1-2]。作为运载火箭主要承力部件，薄壁加筋柱壳轻量化设计可大幅提高火箭运载能力和节约发射成本，但目前我国箭体加筋柱壳结构的设计手段仍以工程手册和经验设计为主，再辅以有限元校核分析及地面试验，缺乏具有针对性的高效优化设计方法[2-4]。特别地，对于我国目前正在研制的长征九号重型运载火箭，其箭体舱段直径达9.5 m，起飞质量达4 000 t级，起飞推力达5×107N级[5-6]，大直径大载荷的结构特点将给箭体结构轻量化设计带来严峻挑战。

对于承受轴向载荷的薄壁加筋圆柱壳结构，整体失稳往往先于结构强度破坏发生，是结构破坏的主要形式，这就使得轴压稳定性成为设计该类结构的重点[7]。Donnell等[8-9]从求解非线性大挠度方程出发，针对薄壳柱壳结构后屈曲分析方法开展了相关研究。李庆亚等[10-11]从理论上对比研究了隐式弧长法、隐式动力学、显式动力学三种常用分析后屈曲问题的数值方法，并基于显式动力学方法对轴压作用下薄壁圆柱壳结构开展后屈曲分析研究。王博等[12-17]采用非线性显式动力学分析方法，对5 m及以下直径运载火箭中的加筋壳结构进行分析，并基于代理模型和等效刚度模型进行优化设计。范书群等[4]基于非线性显式算法对蒙皮桁条结构的中间框尺寸进行了优选设计，理论分析结果与实验结果一致性较好，验证了该分析方法的有效性。从公开文献来看，目前主要是针对5 m及以下直径的运载火箭薄壁加筋柱壳开展研究，当直径达10 m级甚至以上时，薄壁加筋柱壳径厚比将是以往结构2～3倍，其带来的稳定性问题将更为突出，针对该问题的研究尚少。蒙皮桁条结构设计变量众多，涉及离散的拓扑和连续的尺寸优化，其轻质优化问题是典型的混合整数非线性规划问题，且随着结构尺寸的跨越式提高，大直径蒙皮桁条结构后屈曲分析与优化效率将受到极大挑战[17]，因此亟须针对大直径蒙皮桁条结构开展轻质优化设计研究。

本文以我国未来大型或超大型运载火箭薄壁加筋结构设计为背景，针对大直径大载荷蒙皮桁条结构开展结构轻量化研究。基于Python语言建立蒙皮桁条结构全参数化模型，研究了不同加载速度对大直径蒙皮桁条结构后屈曲行为的影响规律。针对蒙皮桁条结构轻质优化涉及离散的拓扑和连续的尺寸优化问题，将该优化问题转化成含非线性性能约束的参数优化问题，提出了基于径向基近似模型和多岛遗传算法加非线性二次规划算法的混合优化策略求解转化后的优化问题，获得了可行的优化解。

1 轴压后屈曲分析及优化问题描述

1.1 非线性显式后屈曲分析

对于一个显式动力学分析，运动方程如式(1)所示。

(1)

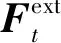
采用中心差分法对控制方程进行显式的时间积分，应用一个增量步的动力学条件去计算下一个增量步的动力学条件。

at=(Ut-Δt-2Ut+Ut+Δt)/Δt2

(2)

Vt=(Ut+Δt-Ut-Δt)/(2Δt)

(3)

其中，Δt为时间增量。

将式(2)和式(3)代入式(1)中，则原运动方程可改写成：

(4)

从式(4)可以看出，增量步结束时的状态仅取决于该增量步开始时的位移、速度和加速度，在时间上“显式地”向前计算位移、速度和加速度，因此不存在收敛性问题。

典型加筋柱壳结构轴压下位移-载荷曲线如图1所示，随着载荷逐步增大，结构可能呈现出线性前屈曲—非线性后屈曲—压溃破坏行为，结构进入线性前屈曲后仍可继续承载，直至整体压溃破坏，压溃破坏后结构承载力急剧下降后趋于稳定[18]。相比于弧长法和隐式动力学方法，显式动力学方法可以稳健地跟踪轴压薄壁结构的后屈曲及后压溃路径及行为，并能与试验结果吻合较好[19]。

图1 典型加筋柱壳轴压位移-载荷曲线Fig.1 Schematic of load versus end-shortening curve for typical stiffened shell

1.2 蒙皮桁条结构有限元建模及其极限载荷计算

作为运载火箭典型的加筋柱壳承力结构，蒙皮桁条结构主要由端框、中间框、桁条和蒙皮组成。蒙皮内侧沿高度方向等间距对称分布4个“Ω”形截面的中间框，2个“L”形截面的端框，同时，蒙皮外侧沿环向均匀分布“工”形截面的竖向桁条，端框、中间框及桁条截面形式如图2所示。

蒙皮桁条结构主要通过桁条来提高结构轴压承载能力，而蒙皮的作用主要是维形和支持桁条。且蒙皮在较小的载荷下会局部失稳和局部进入塑性状态，结构仍能继续承载，直至结构发生整体压溃破坏，其极限承载力由结构整体失稳和后屈曲状态决定。

本文基于Python语言对蒙皮桁条结构进行参数化建模[2]。由于蒙皮桁条结构常使用较薄的蒙皮和桁条，结构上体现为板壳特性，为了能够准确模拟桁条局部截面平动和转动，采用壳单元划分网格，且桁条腹板高度方向划分两层单元[20]。模型边界条件及加载条件如下：模型上下端面中心点各建立一个参考点，并分别与上下端面节点进行刚性耦合，在下参考点处进行固支约束，在上参考点处约束除轴向位移外的其余自由度，轴向匀速施加35 mm强迫位移。模型选用铝合金材料，弹性模量为70 GPa，泊松比为0.3，密度为2.78×10-6kg/mm3，屈服应力440 MPa，强度极限为550 MPa，延伸率为6%。参照以往火箭蒙皮桁条结构设计方法，通过初步结构优化设计，确定蒙皮桁条结构初始设计结构参数，如表1所示。

表1 蒙皮桁条结构初始设计结构参数(1)表格中NHT表示桁条数量，其余设计变量名含义如图2所示。Tab.1 Initial design parameters of skinned purlin structure

采用显式非线性屈曲算法求解该结构极限承载能力时，失稳载荷和失稳模态均与加载速度相关，因此分别采用不同的加载速度对该模型进行分析，并观察结构内部动能与内能的比值，确保加载过程为准静态加载。计算采用4核2.9 GHz主频CPU及8 GB内存的计算机。图3和表2分别给出了加载速度为600 mm/s、300 mm/s、150 mm/s、100 mm/s(即分别在0.05 s、0.1 s、0.2 s、0.3 s内将位移值从0 mm施加到30 mm)时的载荷位移曲线、动能与内能的比值随加载位移的变化曲线、结构失稳位移云图、极限载荷以及计算耗时。

从图3(b)可以看出，对于不同的加载速度，结构内部动能与内能的比值在加载过程中均小于5%，加载之初的峰值是由结构从无载荷状态突然进入到有载荷状态引起的，随着加载继续，该峰值逐渐减小，曲线趋于平稳；加载后期的峰值是由载荷达到结构承载极限后，结构突然发生整体失稳引起的，可以认为是准静态加载。从图3(a)及表2可以看出，随着加载速度变小，结构极限承载能力(曲线的峰值)逐渐减小，对应的加载位移值也逐渐减小，且加载速度越小，峰值点后载荷位移曲线越陡，说明结构达到极限载荷后便迅速发生整体失稳。

(a) 端框(a) End frame

(a) 载荷位移曲线(a) Load-displacement curves

(a) 结构质量灵敏度(a) Sensitivity analysis of the structural mass

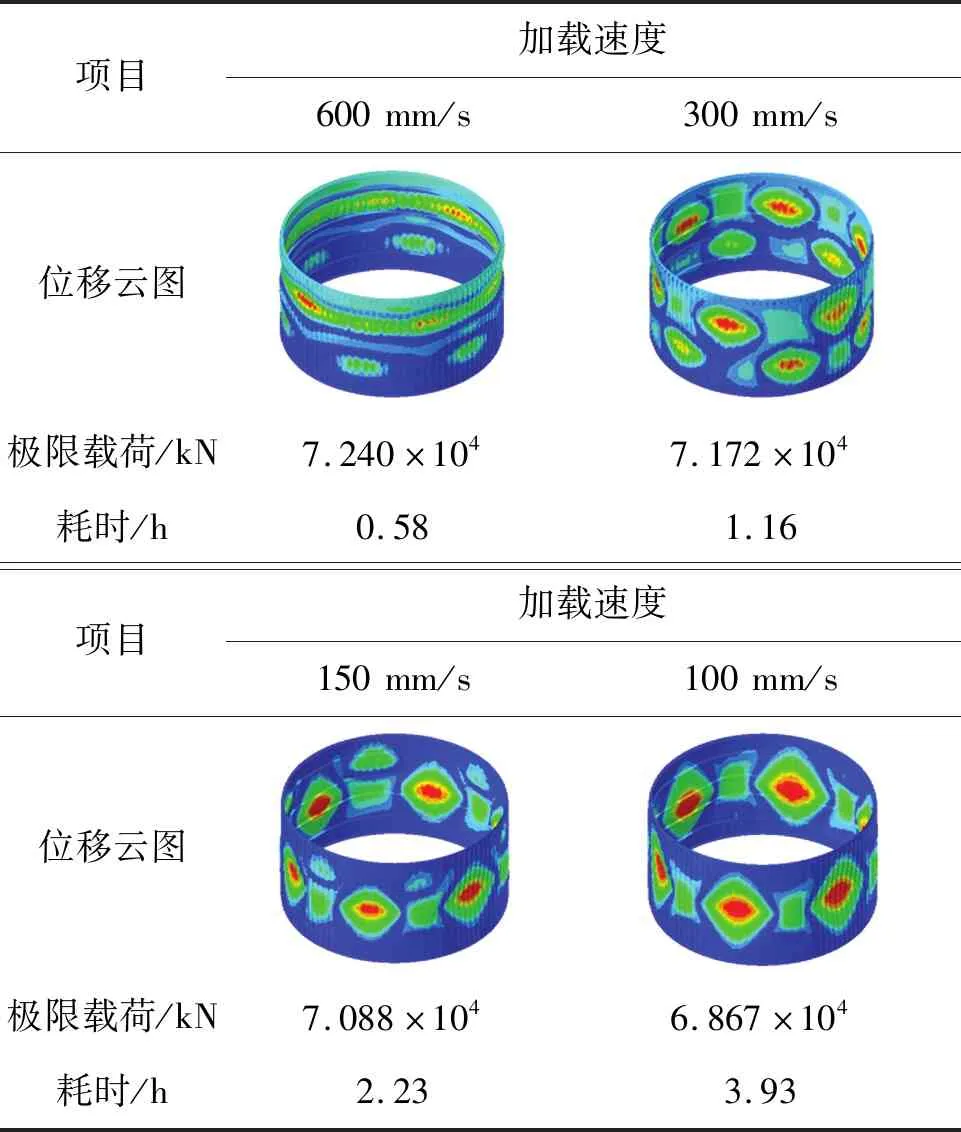
表2 不同加载速度下结构整体失稳情况Tab.2 Overall instability in different loading speed

经大量试算可知，当加载速度小于150 mm/s时，减小加载速度对极限载荷的影响小于4%，结构失稳波形相同，但计算耗时成倍增长。因此，综合考虑计算精度和计算效率，在后续优化中加载速度可取150 mm/s。

1.3 蒙皮桁条结构优化问题描述

通常，结构设计优化包含拓扑、形状和尺寸优化。蒙皮桁条结构优化同时涉及拓扑优化和尺寸优化。其中，拓扑优化与桁条数量相关，不同桁条数量决定了蒙皮桁条结构的拓扑形式，属于离散结构拓扑优化；端框、中间框、桁条截面尺寸以及蒙皮厚度是在结构拓扑形式和形状固定的情况下，搜索最优的截面尺寸，属于结构尺寸优化。

考虑到蒙皮桁条结构中桁条沿环向分布的对称性，本文分别将拓扑优化变量和尺寸优化变量转化成整数变量和连续变量，从而将离散拓扑优化和尺寸优化问题转化成混合整数非线性规划问题。因此，蒙皮桁条结构优化问题可以描述为：

findx=[xc,xd]

minf(x)

s.t.g(x)≤0

(5)

式中，xc表示n个连续变量的向量集合。在蒙皮桁条结构优化中，xc表示连续的截面尺寸变量，而xd表示桁条数目变量。

2 基于径向基函数近似模型的序列近似优化方法

2.1 径向基函数近似模型方法

径向基函数(Radial Basis Function,RBF)近似模型[21-22]是由三层结构构成的前向神经网络：第一层为输入层，节点个数等于输入的样本点个数；第二层为隐含层，节点个数取决于问题的复杂程度；第三层为输出层，节点个数等于输出变量的维数。径向基函数网络模型结构如图4所示。

图4 RBF网络模型结构Fig.4 Model structure of radial basis function

基本径向基函数的数学模型为：

(6)

研究表明[22-25]，Gauss分布函数在全局近似能力方面优势明显。因此将采用Gauss分布函数作为基函数，其表示如式(7)所示。

(7)

ω=Φ-1Y

(8)

2.2 基于近似模型和组合优化算法的序列近似优化方法

空间均布性及填充性高的样本点能够以更大的概率捕获近似对象的特征信息，提高近似模型的近似精度[26]。基于优化拉丁超立方试验设计方法选取初始样本点，由于初始样本点难以保证近似模型对最优解的准确预测，因此在优化的过程中需要通过加入新的采样点对近似模型进行更新，逐步提高近似模型的近似精度。

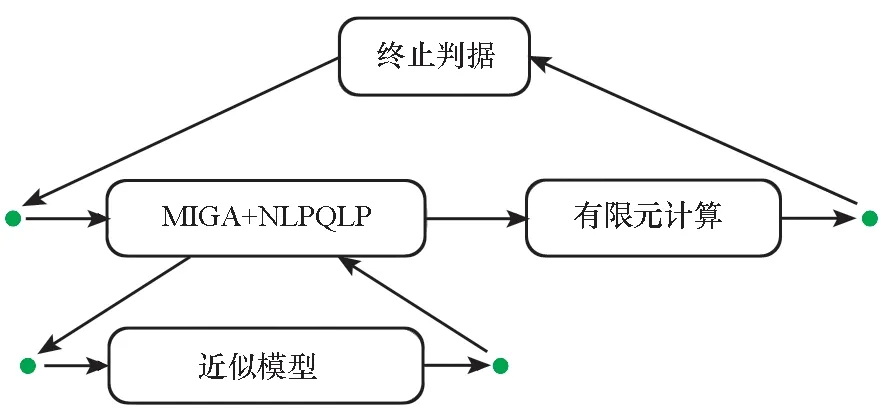
提出的基于径向基函数近似模型的序列优化方法如图5所示。首先利用有限元计算模型获得初始样本点输出值，形成训练样本点集，然后基于训练样本点集构造RBF近似模型并开展优化。基于代理模型和组合优化算法的序列近似优化设计分为：内层迭代优化和外层迭代优化。在内层优化中，采用多岛遗传算法(Multi-Island Genetic Algorithm,MIGA)和非线性二次规划(Non-Linear Programming by Quadratic Lagrangian Programming,NLPQLP)算法对RBF近似模型进行寻优，收敛后进入外层优化；在外层优化中，将内层优化获得的近似最优解作为新的采样点，并调用有限元计算模型进行非线性后屈曲分析，如果有限元计算结果与RBF网络预测的误差满足收敛条件，即小于0.1%，则优化结束，否则将该采样点及有限元计算结果加入样本点集中，更新近似模型，提高近似模型的局部近似能力，并再次进入内层优化，直至内外两层都收敛。

图5 基于径向基函数近似模型优化流程Fig.5 Flowchart of sequence approximate optimization method based on RBF model

在基于近似模型的优化研究中，主要耗时集中在初始样本点的计算上，利用银河超级计算机对构建近似模型的初始样本点进行多节点并行计算，近似模型的构建和基于近似模型优化的耗时仅为单次后屈曲分析的1/10左右，这意味着不仅允许选取更多的初始样本点以提高近似模型全局近似精度，而且可以进行后续采样以更新近似模型，提高其局部近似精度，大大缩短了优化设计周期。

3 蒙皮桁条结构轻质优化设计

3.1 结构参数灵敏度分析

蒙皮桁条结构轻质优化设计影响因素众多，为了从中找出影响结构质量和极限载荷的主要因素，进而实现设计空间缩减并指导后续优化设计，针对蒙皮桁条结构进行参数灵敏度分析。采用优化拉丁超立方实验设计方法选取2 400个初始样本点，利用并行计算资源对不同结构参数下蒙皮桁条结构进行后屈曲分析。设计变量取值范围见表3，图6为样本点在结构质量和极限载荷空间内的分布散点图。

表3 设计变量取值范围Tab.3 Design spaces of design variables

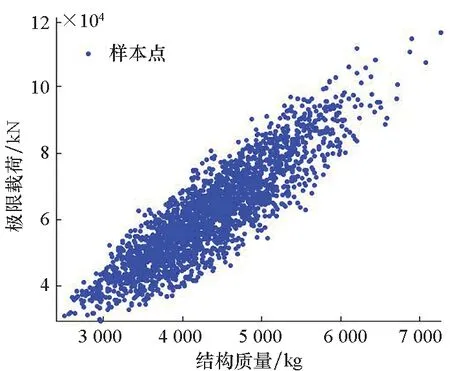
图6 初始样本点分布散点图Fig.6 Distribution scatter diagram of initial sample points

根据上述2 400个样本点的计算结果，首先将各个变量归一化到[-1,1]中，然后基于最小二乘法建立二次回归模型。

(9)

式中：β0，βi，βj和βij分别为对应项系数。

通过将系数归一化，得到不同项对响应的贡献率百分比，即对响应的灵敏度。

Ni=100Si/∑Si

(10)

式中：Si为对应项系数，且∑Ni=100。

基于上述灵敏度分析方法和工程设计经验，对结构质量和极限载荷影响较大的前9个因素分别如图7所示。由结果可知，桁条截面参数以及部分中间框参数对结构极限载荷影响较大，在后续结构优化设计中应重点考虑。

3.2 基于序列近似优化方法的蒙皮桁条后屈曲轻质优化

本节将基于如第2节所述的序列近似优化方法对蒙皮桁条结构进行后屈曲轻质优化。根据3.1节分析结果，并综合工程设计经验，选取如式(1)所示的参数作为优化变量，其他设计变量均取如表1所示的初始设计值，开展蒙皮桁条结构轻质优化设计。蒙皮桁条结构轻质优化数学模型可表示为：

findx

minM

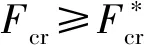
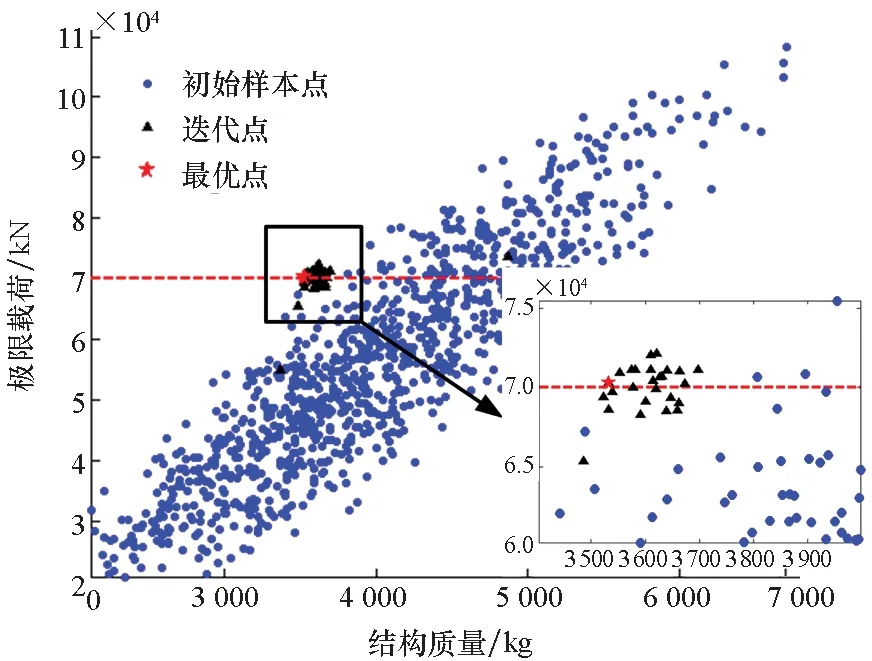
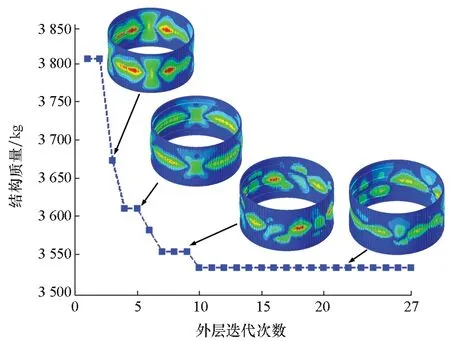
xmin

(11)

为求解如式(11)所示的优化问题，拟采用2.2节所述的基于近似模型和组合优化算法的序列近似优化方法进行研究。通过优化拉丁超立方试验选取1 000个样本点，并调用并行资源计算，获得相应的结构质量和极限载荷。为验证所选样本点空间均布性及径向基函数代理模型全局近似能力，分别从1 000个样本点中随机选取980个样本点构建径向基函数代理模型，并用剩余的20个样本点对代理模型全局近似能力进行检验，该过程独立重复10次，分别评估每次近似精度指标R2值[23,26]，计算结果如图8所示。由计算结果可知，极限载荷和质量的R2值均接近于1，表明所选样本点具有较好的均布性，且构建的径向基函数代理模型具有较高的全局近似能力，可用于后续的结构轻质优化研究。

图8 径向基函数代理模型近似精度Fig.8 Approximate accuracy of RBF model

基于序列近似模型的优化平台如图9所示，其中，经多次试算分析，为提高多岛遗传算法种群多样性和收敛速度，多岛遗传算法中设置岛数为20、每个岛种群数为20，进化代数为40，交叉率为1.0，变异率为0.01，迁徙率为0.01；为提高NLPQLP收敛精度，非线性规划算法设置最小步长为10-4，最大迭代次数为50。

图9 基于序列近似模型的优化平台Fig.9 Optimization platform based on sequence surrogate model

3.3 结果分析

图10为优化后样本点在结构质量和极限载荷空间内的分布散点图，可以看出，每次迭代后近似最优点的极限载荷均在目标极限载荷附近，且结构质量逐渐减小。

图10 优化后样本点分布散点图Fig.10 Distribution scatter diagram of optimal sample points

经过27次迭代，优化结果趋于收敛，目标函数及性能约束的外层迭代优化曲线分别如图11(a)及图11(b)所示，每轮迭代后结构整体失稳模态如图11(a)所示。优化后结构质量为3 530 kg，极限载荷为7.028×104kN，相比于初始设计结构，在承载力满足设计要求的情况下，结构减重273 kg。优化前后结构尺寸如表4所示。

(a) 结构质量迭代曲线(a) Iteration curve of structural mass

表4 初始设计与优化结果Tab.4 Comparison of initial design and optimal variables

4 结论

本文以大型运载火箭结构轻质设计为研究背景，针对大直径大载荷蒙皮桁条结构开展后屈曲轻质优化研究。

基于Python语言对运载火箭级间段蒙皮桁条结构建立参数化模型，为获得结构极限承载能力，采用显式动力学方法对蒙皮桁条结构进行后屈曲分析计算，并分析加载速度对计算精度和效率的影响，确定用于后续优化分析的加载速度。

针对轴压作用下蒙皮桁条结构优化变量多、计算量大的问题，首先，基于优化拉丁超立方实验设计方法对结构参数灵敏度进行了分析，根据灵敏度分析结果，合理地选择了对结构极限承载能力及质量影响显著的设计变量，有效缩减了优化变量维数；然后，提出基于近似模型和多岛遗传及非线性二次规划算法的序列近似优化方法，并对蒙皮桁条结构开展后屈曲轻质优化，获得了工程可行的较优的蒙皮桁条结构设计方案。优化结果表明：相对于初始设计结构，优化后的结构有效减重273 kg，验证了方法的有效性。

后续将在本文的研究基础上开展基于不同桁条截面形式的蒙皮桁条结构轻质优化研究，并针对最优结构形式开展试验验证研究，为大型运载火箭蒙皮桁条结构工程设计提供参考。