复杂海战场环境下AUV全局路径规划方法*

赵 苗，高永琪，吴笛霄，王 鹏，张洪刚

(1.海军工程大学 兵器工程学院，湖北 武汉 430033；2.火箭军工程大学 导弹工程学院,陕西 西安 710025)

自主水下航行器(Autonomous Underwater Vehicle,AUV)路径规划是保证其在水下安全隐蔽航行和可靠高效完成作战任务的关键技术，AUV在执行水下作战任务的路径规划中，需要充分考虑水下环境的不确定性和动态特性以及复杂海战场下的战场地形、自身性能、任务要求、外部威胁、水文信息等多种约束条件限制，近些年逐渐成了国内外学者研究的热点。Li等[1]和Wang等[2]提出了一种基于可视性几何理论的AUV水下路径规划算法，通过模拟典型的水下地理三维实体海洋模型，应用该算法仿真水下三维海洋环境，并进行水下路径规划。Gal[3]提出了一种改进的无人水下航行器(Unmanned Underwater Vehicle,UUV)通视图空间搜索算法，它主要通过减少路径节点的数量来提高算法的计算效率，并融入内部螺旋算法，成功实现水下避障。Arinaga等[4]将Dijkstra算法应用于水下环境中UUV的全局路径搜索，结果表明，该算法可以避免一系列障碍并顺利达到目的，但该试验仅进行了模拟仿真，并未考虑海洋环境对路径搜索的影响。A*算法是全局最短路径搜索最有效的直接搜索解决方法，Li等[5]考虑了海洋环境因素的影响，并用A*算法实现了最优路径的搜索。快速步进算法路径节点间距离的更新采用非线性Eikonal方程简化后的近似偏微分方程，具有较好的可靠性和收敛性。于晖等[6]考虑了UUV的机动约束，将快速步进算法应用于UUV在大范围复杂战场环境中，解决了UUV因导航安全和能耗问题而丢失的搜索路径问题。赵云钦等[7]提出了基于带电粒子模型的航路规划方法，并成功地将该方法运用于UUV的航路规划，有效地解决了多约束复杂海洋环境下的航路规划问题。通过实验表明，该方法能够快速地为航行器规划出可行航路。上述方法的共同缺点是，需要建立复杂的环境模型和未考虑海流等情况，更难以应用于复杂三维动态环境下的在线实时路径规划，搜索效率较低。

基于生物智能算法的航路规划方法不必建立复杂的环境模型，在稳定收敛的同时，可以在自由空间进行随机搜索。Jung等[8]将粒子群优化(Particle Swarm Optimization,PSO)算法的应用推广到三维路径规划中，初始运动由当前位置与目标点的直线代替，通过最小化敌方威胁和燃料消耗获得路径最优解，最后利用B样条曲线得到一条光滑的最优路径。Moreno和Castro[9]提出一种增长的弹性神经网络，用于计算路径规划解。该方法用自组织、网络互连的神经元集合表示路径，各处理单元用Kohonen网络进行局部采样与学习，采用简单的强化规则进化避碰路径，最终得到一条完整的路径。基于生物智能算法的方法可以解决异常复杂的非结构化约束和各种难以近似处理的动力学约束等难题[10]，对于大范围复杂环境下的AUV路径规划问题，生物智能算法仍是解决非确定性多项式(Non-deterministic Polynomial,NP)路径规划问题的有效方法。

1 AUV路径描述和模型建立

1.1 AUV路径的问题描述

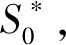
(1)

式中：pi为S=(p1,p2,…,pn)中的路径节点；J表示路径的代价函数；Obstacle表示障碍物约束；Risk表示水下的敌方武器威胁。

1.2 AUV路径规划策略

AUV路径规划首先通过建立空间环境数学模型来表达路径的搜索空间，并给出合适的代价评估函数，然后利用某种算法来寻求这种代价下的最佳路径。减小搜索空间是快速高效地规划出满足AUV机动性能以及作战要求路径的重要手段，众多文献中往往只考虑二维平面内的路径搜索，或是将水平面和垂直面分开路径搜索，但这样很难应用于AUV执行近海底突防、地形跟随以及威胁回避任务。因此，借鉴文献[12]中提出的无人机突防过程中最小威胁曲面的概念，将最小威胁曲面等效为AUV航行的最佳航行曲面。

假设水下地形可以用函数f(x,y)来表示，AUV避免撞底的最佳离底高度用Hc来表示，三维最佳航行曲面可表示为：

F(x,y)=f(x,y)+Hc

(2)

由于实际中获取的水下地形数据是离散的，因此必须通过拟合或者插值的方法得到最佳航行曲面。此外，真实的海底地形复杂，在AUV水下航行中，考虑到AUV的自身机动性能限制，当突遇一个起伏较大的海槽或岛礁时，由于近海底航行离地高度的限制，往往难以避开而发生碰撞。因此，构建的三维最佳航行曲面必须是一个光滑的曲面，Kriging插值算法是一种光滑的插值算法，采用该算法来构建三维最佳航行曲面。

给定起点和终点后，最佳航行曲面上的任意一条曲线都可以看作是一条规划路径，而每一条路径在水平面内的投影也是一条曲线，只要找到水平面内的路径投影曲线，即可在最佳航行曲面上找到相应的最佳路径。文献[13]采用B样条曲线插值方法，在路径规划中只需给出几个控制点就可以得到一条复杂的光滑曲线，然后通过对得到的B样条曲线节点向量的非递减参数等步长的均匀划分，就可以得到一系列的路径节点，这种方法把路径规划问题转化为搜索几个控制点的简单问题，可以大大降低问题求解的维度。本文同样采用B样条曲线方法来描述投影路径，通过确定N个路径控制点来规划一条路径，则每个路径控制点可由极坐标的方式来表示：

(3)

式中：Lst表示起点和终点在水平面内投影的距离；Xi、Yi分别表示第i个路径控制点的横、纵坐标；θi表示水平面内控制点到起点连线与起点到终点连线之间的夹角，其中θi∈[0,2π)。通过搜索N-2个角度值，便可得到N个路径控制点，再通过B样条曲线均匀划分得到一系列的路径投影节点序列(p′1,p′2,…,p′n)，最后通过投影的一一对应关系，即可在最佳航行曲面上找到相应的三维路径节点序列(p1,p2,…,pn)，这样就得到了AUV的近海底航行路径。

1.3 路径的约束条件和代价函数

1.3.1 路径的约束条件

针对AUV大范围海洋环境下的作战背景，主要考虑以下几方面的约束：

1)战场地形约束。战场地形约束主要指对海岛、暗礁以及钻井平台、水下漂浮物等动静态障碍物的避碰。本文所规划的路径均在水下地形数据构建的AUV三维最佳航行曲面上，在最佳航行曲面的构建中已融合了AUV避免碰撞的最佳离地高度，因此战场地形约束只需考虑障碍物的避碰。将障碍物膨化为规则的圆柱体，障碍物的水平面圆心坐标(x0,y0)，深度上、下限坐标分别为zmax、zmin，障碍物的影响半径为Or,则任一路径节点pi(xi,yi,zi)必须满足：

(4)

2)自身性能约束。为了提高所规划路径的可达性，需要考虑AUV的可操控性，包括最小转弯半径等方面的自身性能约束。因此，所规划路径曲率半径的下确界必须大于AUV的最小转弯半径。采用本文所提方法规划的路径非常平滑，一般可以满足AUV对转弯半径的要求。

3)任务要求约束。路径规划需要考虑完成作战任务要求约束。任务约束要求包括航行时间和燃料消耗。假设AUV等功率匀速航行，则AUV单位时间的能耗是常数，也就是能量消耗正比于航行时间，则能量消耗和航行时间两个目标等价。假设AUV实际航行时间为T，AUV完成作战任务要求的最长时间为Tm max，AUV耗尽燃料的最长航行时间为Tmax，则必须满足：

(5)

4)水文信息约束。水文信息约束主要是指海洋中温度、盐度、海流等对AUV航行的影响，本文主要考虑海流对AUV的影响。在海流环境中，不利的海流会直接降低AUV的航行速度，增加AUV完成任务的航行时间和能源损耗，甚至威胁AUV的航向安全；相反，有利的海流可以提高AUV的航向速度，实现快速节能。因此，海流对AUV的航行约束可以转化为规划路径代价函数中的航行时间，以此来满足海流的约束。

5)武器威胁约束。武器威胁约束主要是指敌方声呐、海底水听器的探测威胁和敌方水雷阵、反AUV等火力威胁。敌方武器威胁包括被敌方探测类武器侦察威胁和敌方火力杀伤威胁[14]。被敌方探测类武器侦察的时间和概率直接影响着AUV的航行安全，因此将敌方探测类武器侦察的有效时间作为规划路径代价函数的一部分。敌方火力杀伤威胁：一种是敌方布放水雷等杀伤性武器密集区域形成的禁航区，本文按照水下障碍物模型进行等效处理来满足约束；另一种是敌方武器平台携载杀伤性武器的威胁，同样转化为代价函数的一部分作为优化目标进行约束。

1.3.2 路径的代价函数

在对AUV进行路径规划之前，必须确定路径规划的性能指标。在AUV执行作战任务过程中，希望AUV航行的路径具有以下性质：规划路径航行时间尽量短，满足作战任务要求；规划路径被敌方有效侦察时间尽量少；规划路径被敌方有效杀伤的时间尽量少，满足AUV自身航行的安全性。

1)航行时间代价：由上一节在AUV的路径描述中，路径中的节点坐标pi是采用B样条曲线方法并通过一系列控制点生成的。研究使用的三维空间海流是由一组基于多重涡流和Navier-Stokes方程来模拟的[15-16]。假定在静态海洋中AUV的速度是恒定的，海流的速度为VC，AUV的航行速度Va运动方向为从节点pi指向节点pi+1，则三个速度矢量的空间关系可由图1具体描述。

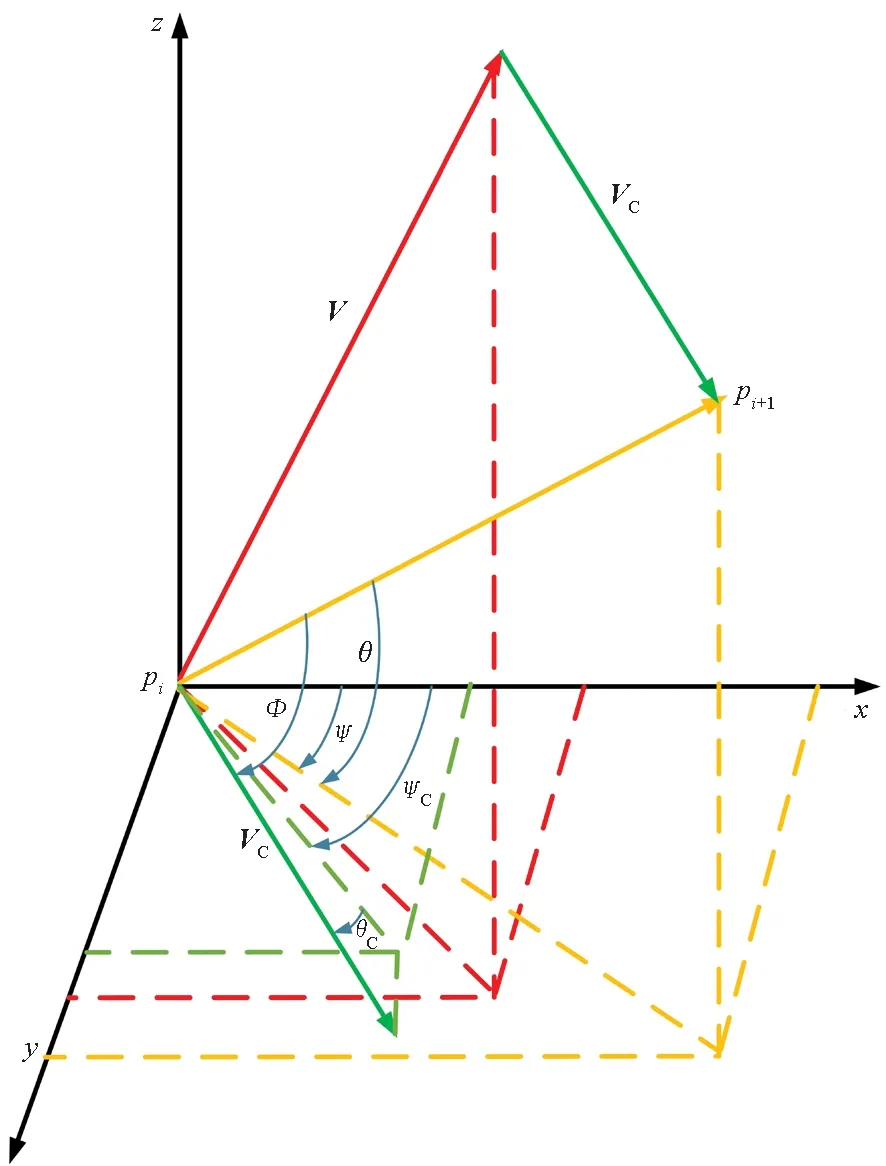
图1 AUV速度合成示意图Fig.1 Schematic diagram of AUV speed synthesis

由图1可知，海流速度VC的三个方向矢量(uC,vC,wC)可以表示为：

(6)

其中,θC、ψC分别表示海流速度在水平和垂直方向上的夹角。将AUV航行速度在水平和垂直方向上的夹角分别记作θ、ψ，AUV航行速度与海流速度的夹角为Φ，则AUV航行速度在三个方向上的速度矢量(u,v,w)和夹角Φ可以表示为：

(7)

由式(6)和式(7)可推导出：

(8)

则AUV的航行时间代价为：

(9)

2)敌方有效侦察时间代价：AUV的隐蔽性是其在海战场中执行作战任务最重要的战技术指标之一，因为被敌方声呐探测侦察很可能会导致作战任务失败，甚至对作战造成不可估量的损失。因此，在路径规划中必须考虑在执行任务时被敌方声呐有效侦察时间，具体可以表示为：

(10)

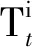
3)敌方有效杀伤时间代价：在AUV执行任务时，敌方杀伤性武器装备的部署直接对AUV造成威胁，因此敌方杀伤性武器对AUV的有效杀伤时间是路径评价指标的重要组成部分。敌方有效杀伤时间代价可以表示为：

(11)

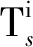
在AUV路径规划时，需要满足并且最优化上述提到的所有性能指标，但是要使所有性能指标都达到最优是不可能的，因为某些目标就是矛盾的，比如安全性和航行时间。通常的做法是使用加权求和法。因此，本文选择的代价函数J为：

(12)

其中，w1、w2、w3分别表示AUV航行时间、被敌方有效侦察时间和有效杀伤时间的权重系数，权重系数一般通过多次试验给定。在这里需要特别说明的是，本文假定在两个连续路径节点pi和pi+1之间的任意路径点的海流速度、被敌方侦察的概率、杀伤概率与路径节点pi+1处完全相同。

2 基于振荡型IWO算法的全局路径规划

本文中AUV的航行路径是一条在水平面内投影为一组控制点定义的B样条曲线构成的三维路径。在给定起点和终点后，路径规划问题的本质转化为通过优化算法来寻找一组最优控制点的问题。在路径规划中遇到密集的障碍物、起伏较大的地形区域等情况时，将导致可行路径解的空间范围变小，使得算法在搜索路径时很容易陷入局部最优解，导致规划路径的质量降低或无效路径的产生。IWO算法是Mehrabian和Lucas于2006年提出的一种从自然界野草进化原理演化而来的随机搜索算法[17]。2010年，Basak等提出了一种改进型的振荡型IWO算法[18]，在计算标准方差(Standard Deviation,SD)的过程中引入一个振荡因子|cose|，使得算法得在全局搜索和局部搜索并行展开，相比IWO算法，全局寻优能力和快速收敛性都得到了极大的提升。因此，本文采用振荡型IWO算法作为路径规划的搜索算法。

2.1 基于振荡型IWO算法的路径规划基本原理

路径规划问题的最终目标是要在规划空间中得到满足要求的一个解向量。因此在振荡型IWO算法中，每株野草的位置都被视为规划空间中的一个解，并且解代表的路径优劣程度由上文的路径代价函数来进行度量。通过代价函数值计算每株野草产生的子代数量，每株子代野草的位置由父代野草的位置和当前代的标准方差值决定，通过不断淘汰适应度值差的野草，更新标准方差值，提高算法的收敛速度和自适应能力。记野草的初始种群数量为A，它由n株野草组成：{a1,a2,…,an}，每株野草aj=(θ1j,θ2j,…,θnj)代表规划空间中的一条航路。对于任意一株野草aj，可以计算得到该野草所代表航路的代价函数fj。同样对于整个野草种群，其中每株野草位置的代价都可以根据式(13)计算得到：

f=[f1,f2,…,fn]

(13)

故而可以根据代价函数值得到该野草种群中适应度最好的野草abest和最差的野草aworst，以及它们的代价函数fbest和fworst：

(14)

适应度较好的野草相比于适应度较差的野草应该在搜索寻优过程中发挥更重要的作用。因此，每株野草产生后代的数量可以和代价函数值关联起来。在迭代过程中，每株野草产生的子代数量、子代野草的位置以及当前代的标准方差更新计算方法如下。

1)种子产生的数量。对于野草aj产生种子依据本身以及野草种群中适应度最好的野草abest和最差的野草aworst计算每株野草繁殖种子的数量：

(15)

式中，[·]表示取整。

可以看出，适应度值越好的野草其代价函数值越小，所产生的种子数量越多。这使得种群中适应度越好的野草越来越多，进而使适应度较差的野草被淘汰。

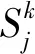
(16)

其中，normrnd(aj,σe)是以aj为均值，σe为方差的正态分布随机数。

(17)

2.2 基于振荡型IWO算法的路径规划步骤

基于振荡型IWO算法的路径规划方法具体步骤描述如下。

步骤1：根据实际问题设置选择合适算法参数需要确定种群的初始数量Pinitial、种群的最大数量Pmax，最大迭代次数emax、最大和最小种子数量Smax和Smin、非线性指数n、标准方差的初始值σinitial和最终值σfinal以及算法终止条件。

步骤2：根据路径规划任务的要求设置算法问题维数D，野草种群初始化，初始化每株野草位置。

步骤3：根据设定的代价函数，按规则计算出每株野草的适应度值，并计算出种群中适应度最好的野草的代价函数值fbest和最差代价函数值fworst。

步骤5：当种群数量达到上限时，对种群中所有的野草按代价函数值大小排序进行淘汰，保留适应度值最好的Pmax株野草。

步骤7：判断是否到达最大迭代次数emax，如果没有，返回到步骤4，否则算法结束。

步骤8：输出全局最优代价函数值的野草所代表的航路。

3 仿真结果与分析

将式(12)采取的代价函数作为优化目标为AUV搜索全局最优路径；每种算法运行100次，通过蒙特卡洛模拟实验，对IWO算法、振荡型IWO算法、全振荡型IWO算法以及粒子群算法四种路径规划算法计算所得的路径平均代价值和标准方差进行比较。

计算机仿真平台为MATLAB 2016a，处理器为酷睿i7-3630QM，@2.40 GHz，RAM8 GB，操作系统为Windows7-64位。标准IWO算法、振荡型IWO算法、全振荡型IWO算法以及粒子群算法四种算法的种群规模统一设置为N=30，最大迭代次数emax=500，控制点的个数统一设为12，则问题的维数D=10，算法的参数设置如表1所示。

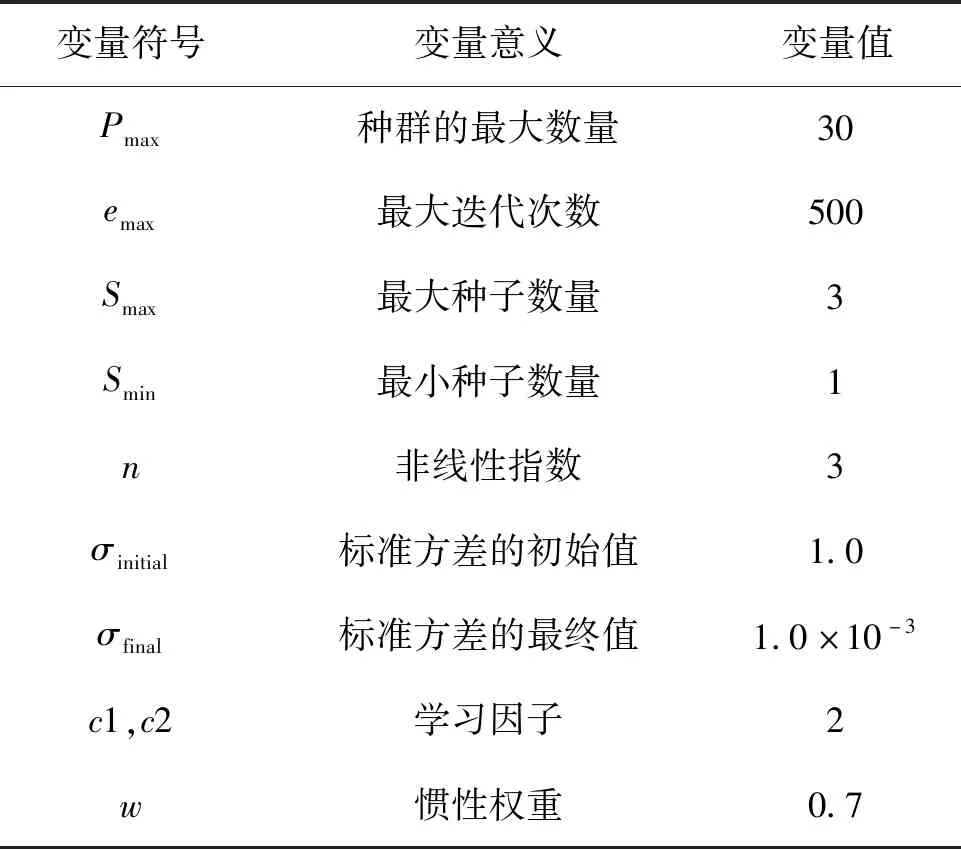
表1 算法的参数设置Tab.1 Parameter settings of the algorithm

仿真试验选取116.8°E～117°E，23°N～23.2°N区域为路径规划区域，水下地形的原始数据采用美国Scripps海洋研究所公布的分辨率为1海里的数据。首先利用移动Kriging插值算法获得分辨率为100 m的水下高程地形数据，利用Kriging插值算法构建AUV最佳航行曲面。这里需要特别说明的是，考虑到获得的水下地形数据分辨率较高，本文将任务区域的经纬度坐标转换后缩小为原来的1/100形成实验的水下地形，这样可以更加直观真实地反映水下威胁的探测范围，便于仿真试验的开展和研究；AUV的航行速度设置为9.252 m/s；海流采用20个涡流叠加而成，敌方武器威胁由水雷等密集布放的武器平台构建的禁航区、敌方水面舰艇和潜艇来模拟；障碍物由水中漂浮物来模拟。具体水下威胁模型参数设置如表2所示。

表2 水下威胁空间的参数设置Tab.2 Parameter settings for underwater threat space

设置任务的起点为(132 800 m,25 360 m,-80 m)，终点为(133 300 m,25 500 m,-80 m)，分别设置算法的种群初始数量为10、20，仿真得到的AUV规划路径如图2、图3所示，不同算法的代价函数值收敛曲线和各路径性能指标分别如图4和表3所示，不同算法参数下的最优路径、路径的平均代价函数值和标准方差如表4所示。需要特别说明的是，仿真图中蓝色线条构成类半球状图形表示武器平台的最大探测范围，红色线条构成的类半球状图形表示武器平台杀伤性武器的杀伤范围，黄色圆柱体表示禁航区的范围，青蓝色圆柱体表示障碍物的影响范围。

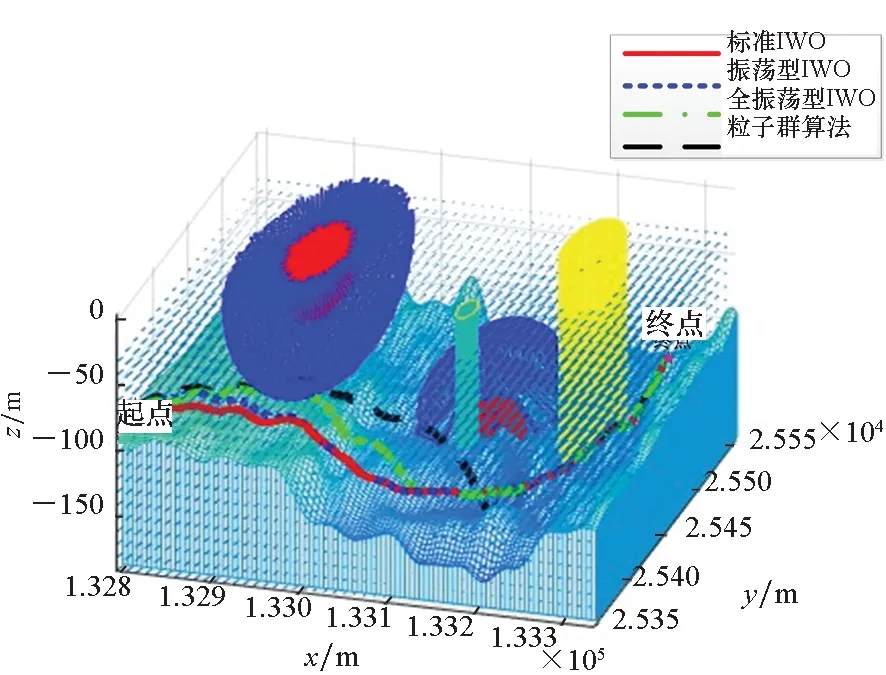
图2 不同算法规划的最优路径三维立体图Fig.2 Three-dimensional perspective of the optimal planning path of different algorithms

图3 不同算法规划的最优路径三维俯视图Fig.3 Three-dimensional top view of the optimal planning path of different algorithms

图4 不同算法的代价函数值收敛曲线Fig.4 Cost function value convergence curve of different algorithms

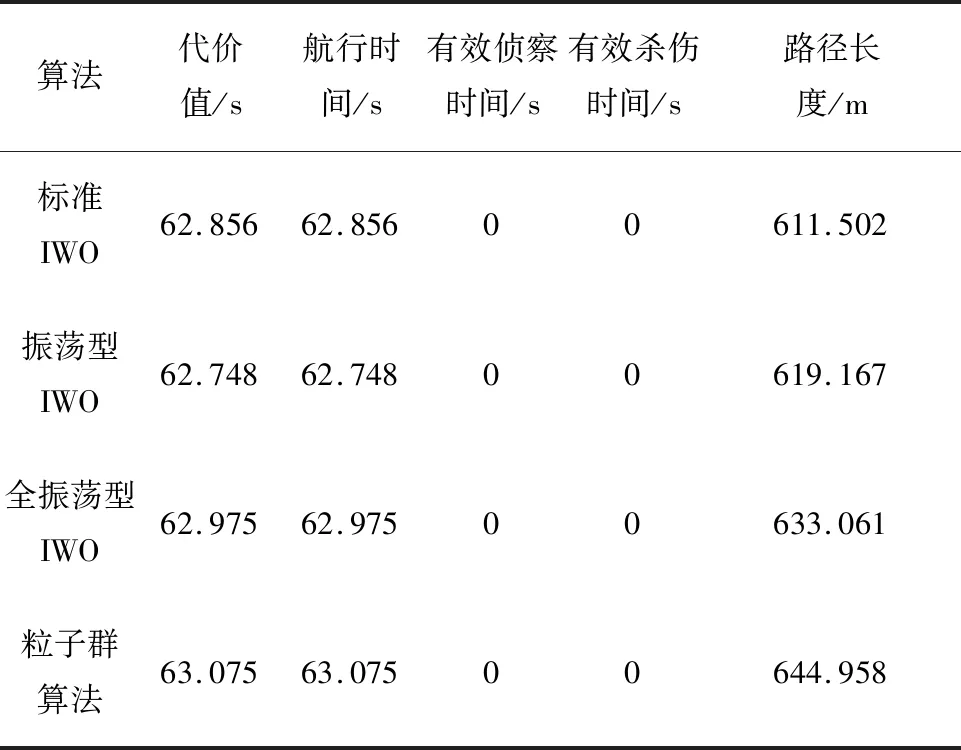
表3 不同算法最优规划路径的性能指标值Tab.3 Performance index values of optimal paths of different algorithms

表4 运行100次不同规划算法的路径代价比较Tab.4 Path cost comparison of different planning algorithms running 100 times

通过图2、图3可以看出，采用四种算法为AUV规划出的最优路径均能绕过敌方探测、火力威胁以及禁航区，并成功躲避水下障碍物后安全抵达任务终点。在不同算法规划路径的代价函数值差别不大时，振荡型IWO算法比标准IWO算法规划的路径长度长7.665 m，航行时间少了0.108 s，这说明振荡型IWO规划的路径较好地利用了海流来引导AUV航行，增大了航行速度，从而减小了航行时间。通过表4可以看出，选取标准IWO算法、振荡型IWO算法、全振荡型IWO算法的初始种群数量为10、20，粒子群算法的初始种群数量为20，分别运行100次，发现标准IWO算法存在陷入局部最优的现象，而振荡型IWO算法规划最优路径优于其他三种算法，平均路径代价振荡型IWO算法最优。从标准方差来看，振荡型IWO算法的稳定性也更好，这是由于振荡型IWO算法的标准方差随着迭代次数的增加呈振荡衰减的趋势，当在迭代初期，如果野草靠近一个可疑的最优解，引入一个振荡因子后就会使标准方差处于相对较小值，从而实现快速的局部搜索，而不是等到迭代后期标准偏差降低到一个合理的值再进行，这样有很大的概率可快速地发现较优解，使得算法在迭代初期也可以进行局部搜索，提高了IWO算法的寻优能力，因此基于振荡型IWO算法路径规划方法的规划效果最好。

4 结论

本文介绍了基于振荡型IWO算法的AUV路径规划方法的基本原理，结合复杂海战场环境，提出了一种以构建最佳航行曲面为条件，基于振荡型IWO算法的三维路径规划方法。仿真实验表明，该方法可以高效、准确地为AUV水下作战任务规划出一条满足性能要求的最佳路径。该方法未来可以广泛应用于AUV执行各种水下近海底突防、地形跟随以及威胁回避等不同作战样式下的全局路径规划任务。