OFDM/OQAM系统信道估计改进方法*
刘永进,陈西宏,赵 宇
(空军工程大学 防空反导学院,陕西 西安 710051)
作为一种经典的多载波调制技术,正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术一直以来备受关注。它的优势主要在于频谱效率更高[1]和可操作性更强[2-4]。但OFDM仍然存在一些不足,最典型的就是符号间干扰和载波间干扰(Inter-Symbol Interference and Inter-Carrier Interference,ISI/ICI)。为了弥补OFDM的不足,同时保持它的优势,提出了基于交错正交幅度调制的正交频分复用(OFDM based on Offset Quadrature Amplitude Modulation,OFDM/OQAM)技术[5-7]。
OFDM/OQAM只在实数域正交,能够引入各种不同的原型滤波器,并且不需要插入循环前缀[8]。OFDM/OQAM具有与OFDM相同甚至更高的信号传输效率。因此,近年来对于OFDM/OQAM的研究越来越多[9-11]。但是,只在实数域正交将会给系统带来更为严重的符号间干扰,进而影响系统的信道估计精度。因此,对于OFDM/OQAM来说,如何克服干扰的影响以提高信道估计精度是一个亟待解决的问题。针对OFDM,目前已有很多对应的信道估计方法。考虑到OFDM/OQAM与OFDM的相似性,这些方法能够提供一些借鉴。
针对OFDM/OQAM,目前已经提出了很多的信号估计方法[12]。文献[13]通过将保护符号放置在导频的不同侧边设计了两种信道估计方法。这两种方法都能够取得较好的信道估计效果,但保护符号降低了系统的频谱效率。为了解决这一问题,文献[14]设计了一种编码辅助导频,该导频不仅能够携带传输数据,提高传输符号利用率,同时能够消除虚部干扰,但该导频结构需要占用2~4个时隙,造成了频谱资源的浪费。
为了提高系统频谱利用率,压缩采样法被引入信道估计中。文献[15]在系统稀疏度未知的条件下,设计了一种自适应压缩采样匹配方法筛选目标集,提高了信道估计的精度,但该方法复杂度高,实用性差。文献[16]同样是在压缩采样的基础上,提出了基于干扰近似法和基于成对导频的信道估计两种方案,这两种方案都能够提高系统的信道估计性能。系统稀疏性的证明是这两种信道估计方案的关键,但系统是否具有稀疏性是不确定的,这限制了压缩采样法在信道估计方面的应用。无论哪种信道估计方法,都需要减小或消除系统固有干扰对信道估计的影响,从而提升系统信道估计精度,兼顾系统频谱利用率的提高。
为了消除固有干扰,通常会在导频和数据符号之间插入0值导频,但0 值导频的插入降低了系统的频谱效率。在文献[17]所提导频结构的基础上,本文设计了一种频谱效率更高的导频对信道进行估计。该导频结构的伪导频功率更高,信道估计性能更好。
1 经典的OFDM/OQAM系统信道估计模型
根据文献[18],连续时间OQAM基带传输信号可以表示为:
(1)
式中:M代表子载波数,am,n代表在符号时间m子载波n所传递的实数符号,g(t)代表脉冲成型滤波器函数;ν0代表子载波间隔,τ0表示一个OQAM信号相邻实部和虚部的时间偏移,ν0=1/T0=1/(2τ0),其中T0代表复数符号的周期;φm,n为附加随机相位[2],
(2)
其中φ0可以随机选择,为方便讨论又不失一般性,令φ0=0。
为了完美重构信号am,n,OQAM系统必须满足式(3)所示的正交条件[2]:
=δm,p(t)δn,q(t)
(3)
其中,〈x,y〉为x和y的内积,δ(t)为狄拉克函数,Re(·)为取实部操作,“*”代表复共轭。在无失真信道中,接收信号y(t)与传输信号s(t)相等。在子载波pth时隙qth上传递的复信号[12]为:

(4)

(5)

(6)
在多径信道中,多径效应会给系统带来严重的载波间干扰和符号间干扰。在这种情况下,为了保证在接收端重构传输信号,需要提出对应的信道估计方法。
OQAM信号经过带有高斯噪声η(t)和脉冲传递函数为h(t)的多径信道后,接收信号[16]可以表示为:

g(t-τ-nτ0)dτ+η(t)
(7)
式中,Δ代表信道最大延迟。假设原型滤波器方程在时间间隔τ∈[0,Δ]内变化缓慢,即g(t-τ-nτ0)≈g(t-nτ0),此时式(7)可改写为:
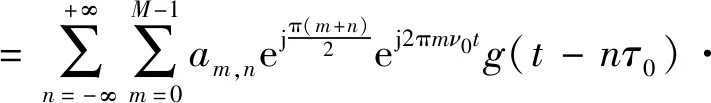

(8)

ym0,n0=〈y(t),gm0,n0(t)〉
(9)

显然,系统的固有干扰包含在〈gm,n(t),gm0,n0(t)〉中。为了分析符号间干扰和载波间干扰对信道估计的影响,应当首先将系统的固有干扰从〈gm,n(t),gm0,n0(t)〉中分离出来。



(10)
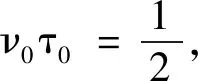
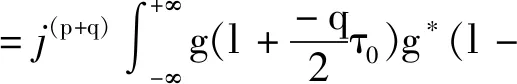

=j(p+q+pq+2pn0)Ag(-qτ0,pν0)
(11)
式中,Ag(τ,ν)是滤波器函数g(t)的模糊度函数,定义为
(12)
由于Ag(τ,ν)为实函数[19],将式(11)代入式(9),可得
(13)

(14)
其中,

(15)
(16)
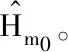
令Cp,q=j(p+q+pq+2pn0)Ag(-qτ0,pν0),am0-1,n0与am0+1,n0设为符号相反。此时式(13)可以改写为:
ym0,n0=am0,n0Hm0+C-1,0am0-1,n0Hm0-1+
C1,0am0+1,n0Hm0+1+
(17)
假设信道为平坦衰落信道,即Hm0=Hm0+1=Hm0-1,则此时系统的信道频率响应为:
(18)

作为基于导频的信道估计方法之一,干扰近似法能够减弱固有干扰对导频的影响。干扰近似法一共分为三类:IAM-R,IAM-I 和IAM-new。图1为IAM-R的结构。

图1 IAM-R的导频结构Fig.1 Frame configuration for IAM-R method
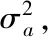
(19)
通过改变导频结构,可以提升伪导频的功率。IAM-I就是在IAM-R的基础上,增加虚数导频符号得到的一种方法。IAM-I的导频结构如图2所示。

图2 IAM-I导频结构Fig.2 Frame configuration for IAM-I method
对于IAM-I来说,伪导频功率[20]为
(20)
如图2所示,处在对称位置的导频符号没有设置为互为相反数,这会降低伪导频的功率。因此,通过重新设置导频结构可以继续提升伪导频的功率。受此启发,提出了如图3所示的IAM-new的导频结构。
随着教育的不断改革与深化,数学教学已经朝着培养学生核心素养全面发展,面对这个问题,除了在设计教学目标和课堂教学之外,很多教师还会在课后练习中为学生留下一些开放性的作业,这样不仅可以激发学生对于数学知识的学习兴趣,巩固学到的数学知识,还能提高他们的应用意识,提升他们的数学核心素养。
图3 IAM-new的导频结构Fig.3 Frame configuration for IAM-new method
通过计算,可以得到IAM-new的伪导频功率如式(21)所示:

(21)
2 改进的导频结构
改进的导频结构如图4所示。

图4 改进的导频结构Fig.4 Frame configuration for the improved method
图4中的导频符号被周围的数据符号包围。式(15)中的I1项会被所有符号所影响,但对于信道估计来说,这是不必要的。
(22)
式(22)说明一阶邻域符号的影响占了绝对比重。根据文献[17],随着|p|和|q|的增大,Cp,q迅速减小,当(p,q)∉Ω3,3时,Cp,q近似等于0。因此,本文只考虑3阶邻域内符号的干扰。此时,式(13)可改写为:
(23)
其中,
(24)
(25)
(26)
首先,根据式(23)得到初始的信道频率响应如下:
(27)
(28)
其中,D[·]为预判决算子。
(29)
(30)
由于am0+p,n0+q的初始值是随机选择的,这使得通过式(30)得到的信道频率响应估计值与真实值之间存在较大误差。为了减小误差,提升信道估计精度,将式(30)得到的估计值代入式(28)中进行第二次的迭代运算。通过多次的迭代之后,误差将会逐渐变小。
综上所述,本文所提出的导频结构能够对OQAM信道进行估计,提升系统的频谱效率。信道估计性能是衡量一个信道估计方法好坏最重要的标准,根据之前的讨论,伪导频功率影响信道的估计性能,因此,通过计算伪导频功率就可以判定本文提出的导频结构的信道估计性能。根据图4,可得伪导频功率为:
(31)
与式(19)相比,式(31)中的导频功率更高。因此,本文所提出的导频结构不仅能够提高频谱效率,还可以提高信道估计性能。
3 仿真分析
调制方式、载波数目、信道条件是影响信道估计性能的主要因素。因此,本节将对不同调制方式、不同载波数和不同信道条件下的信道估计性能进行仿真,从而验证本文所提出的方法的有效性。设A为本文所提出的导频结构和信道估计方法,B为文献[17]提出的信道估计方法,导频功率与数据符号功率比为1.5 ∶1。仿真所需参数值如表1所示。
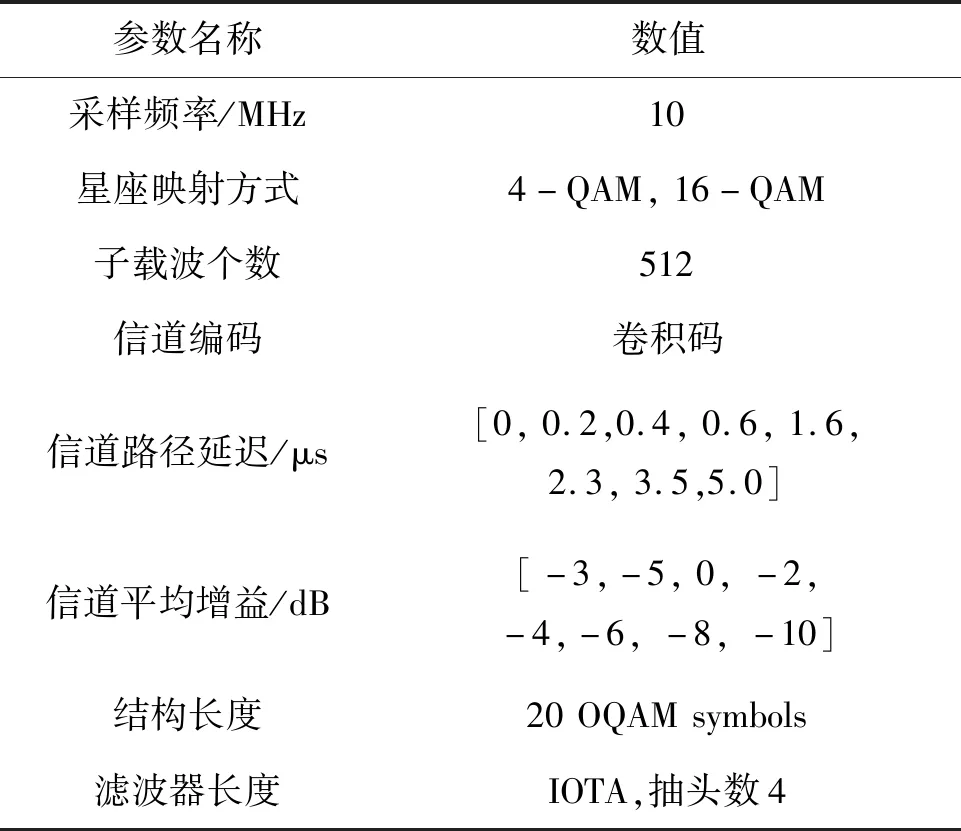
表1 参数设置Tab.1 Fundamental parameters of simulation
图5给出了改进的导频结构 (A) 与IAM方法 (B) 在4-QAM 与 16-QAM两种星座映射调制下的标准均方差(Normalized Mean Squared Error,NMSE)性能。在 16-QAM调制情况下,当信噪比(Signal-Noise Ratio,SNR)较低时(SNR<15 dB),本文提出的导频结构的信道估计性能略优于IAM方法,但优势不明显;随着信噪比的不断增大,本文所提出的导频结构的信道估计性能不断提高,与IAM方法相比,性能优势越来越明显。一方面,这是因为IAM方法存在性能平台,当SNR=15 dB左右时,该方法的性能不再随SNR的增加而提高;另一方面,本文所提出的导频结构具有更高的伪导频功率,随着SNR的增加,伪导频功率不断增大,信道估计性能也随之不断提高。类似地,当采用4-QAM调制时,IAM方法将在SNR=20 dB左右时到达性能平台。可以看出,该条件下本文所提出的导频结构在信道估计性能方面同样优于IAM方法。
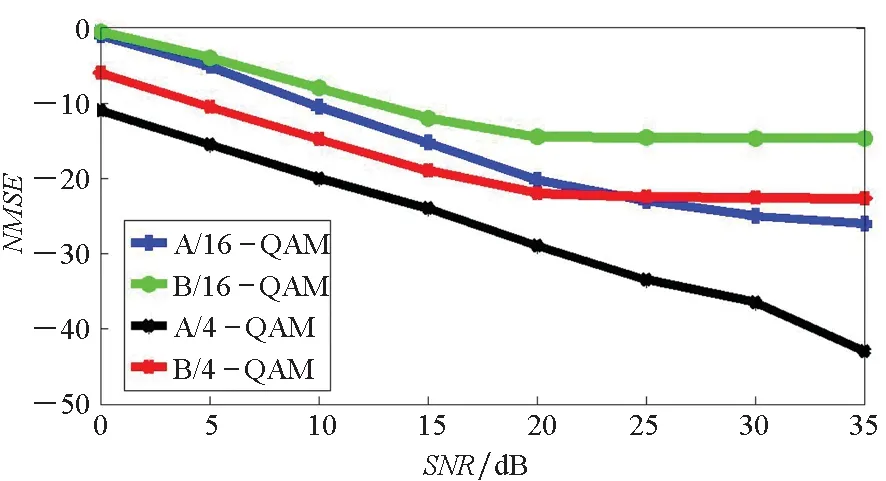
图5 4-QAM 与16-QAM调制下的NMSE性能Fig.5 The NMSE performance with 4-QAM and 16-QAM
从图6也可以得到类似的结论。图6比较了4-QAM与16-QAM两种调制方式下两种方法的误码率(Bit Error Ratio,BER)性能。当BER=10-3时,在4-QAM调制下,方法A比方法B优4 dB;在16-QAM调制下,方法A比方法B优1 dB。随着SNR的增加,两种方法之间的差异变化并不大。上述结果表明本文提出的方法在OFDM/OQAM信道估计方面有优势。
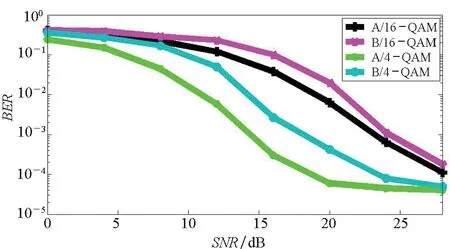
图6 4-QAM 与16-QAM调制下的BER性能Fig.6 The BER performance with 4-QAM and 16-QAM
图7为不同迭代次数条件下方法A的NMSE性能。经过迭代后,信道估计性能明显增强。当迭代次数小于4时,随迭代次数的增加,性能提升明显。但当迭代次数为4和5时,两者之间的性能差异并不大,说明经过4次迭代后,得到的信道估计值已经接近真实值,达到性能上限。与文献[17]只需2次迭代相比,迭代次数有所增加。这是因为本文提出的导频结构只占有一个符号时隙,并未插入0值导频。因此,为了减小固有干扰造成的影响,需要更多次数的迭代才能够逼近真实值。

图7 不同迭代次数条件下的NMSE性能Fig.7 The NMSE performance with different number of iterations
图8为不同子载波个数条件下两种信道估计方法性能的对比。当子载波个数为256时,两种方法的性能没有明显差异;当子载波个数为512时,两种方法的性能曲线差异增大,但仍然近似重合,方法A仍然略优于方法B。两种方法在子载波个数较大时性能更加优良。图9为不同信道条件下方法A与方法B的性能对比,图中WR代表无线区域网络信道,TU代表典型城市信道。图9表明在两种信道条件下,本文所提方法要优于IAM方法。
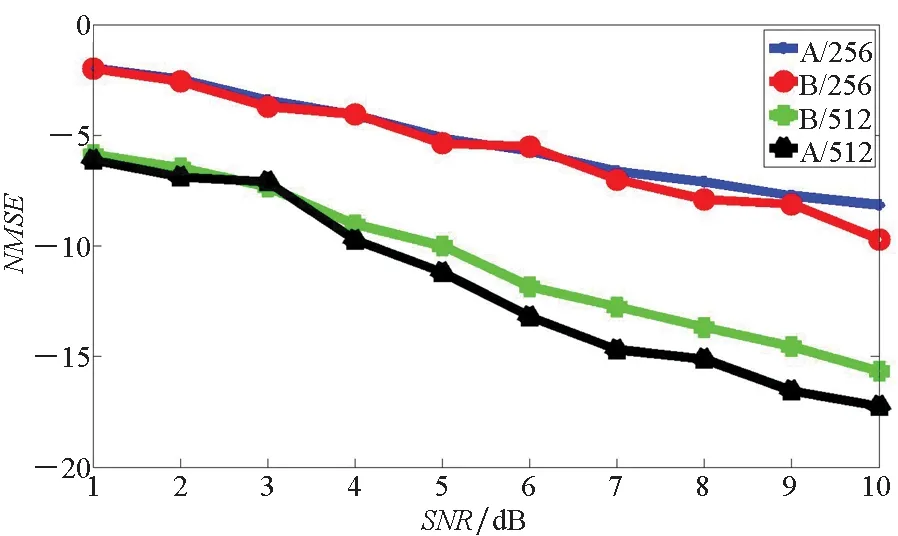
图8 不同子载波个数条件下两种信道估计方法的NMSE性能Fig.8 The NMSE performances of two channel estimation methods with different discrete Fourier transform size

图9 不同信道条件下两种方法的NMSE性能Fig.9 The NMSE performances of two channel estimation methods in different channels
综上所述,与传统的IAM方法相比,由于本文提出的改进导频结构具有更高的伪导频功率,降低了干扰与噪声对信道估计造成的不利影响,因此,在不同调制方式、不同载波数与不同信道条件下,本文方法都表现出更好的信道估计性能。同时,由于只占用一个时隙,本文方法还能够节约系统的频谱资源,提高频谱效率。
4 结论
为了提升OFDM/OQAM系统的信道估计性能,节约频谱资源,本文提出了一种导频结构,并给出了对应的信道估计方法。在分析了已有导频结构的缺点之后,提出了一种伪导频功率更高、仅占用一个时隙的导频结构。为了得到伪导频的参数,利用预判决法对传递信号进行重构。同时引入迭代,减小估计误差。仿真结果表明,本文所提出的导频结构和信道估计方法,能够提升系统的信道估计性能,提高频谱效率。

