融合用户模糊聚类和相似度的加权Slope One优化

石 朋,姚文明,王 祥

(1.中国电子科技集团公司第十五研究所,北京 100083; 2.中国农业银行研发中心,北京 100071)

0 引 言

面对大数据时代的到来，信息的提供者和消费者都遇到了很大的挑战。对于信息提供者来说，由于不知道消费者的具体需求，可能会给消费者提供很多其实并不需要的信息，不但没有给消费者带来便利和帮助，反而变成了消费者眼中的垃圾信息。对于消费者来说，我们处在一个信息爆炸的时代，一方面，大量的信息使我们对于某一类型信息有了更多的选择；另一方面，大量的信息也使我们在寻找意向信息的时候要花费大量的时间和精力，面对日益增长的PB级甚至TB级的数据，就像是大海捞针，力不从心。面对这种情况，信息检索技术的出现大大缓解了“信息过载”的问题，人们通过关键词和主题可以搜索到相关内容的信息，但是由于缺乏用户针对的因素，搜索引擎把检索到的所有信息全部提交给用户，由于数据量巨大，对于用户来说依旧要耗费大量的时间去人工寻找，即又一次出现了“信息过载”的问题。在这种情况下，如果能够根据消费者的历史行为数据分析出用户特征、兴趣度等有价值的信息进行有针对的推荐，既能提高用户体验又能节约用户时间，这对于消费者来说是非常有价值的。于是，个性化推荐系统[1]应运而生。

当下应用范围最广的推荐算法是协同过滤算法[2]，它无须分析内部属性，仅依靠用户历史行为信息就可以完成推荐。协同过滤算法基本可以分为基于用户的协同过滤算法(UBCF)[3]和基于项目的协同过滤算法(IBCF)[4]。UBCF算法理念是将与当前用户相似的人感兴趣评分高的项目推荐给此用户，而IBCF算法理念是将与当前项目相似的项目推荐给目标用户,但存在冷启动[5]和矩阵稀疏[6]时效果不理想的问题。而Slope One算法[7]是Lemire等人在2005年提出的一种基于项目的协同过滤算法，算法形式简洁易懂，扩展性强，能够在一定程度上缓解冷启动的情况，有良好的推荐精度。但是，Slope One算法在计算项目之间的评分偏差的时候没有考虑到用户评价的项目数量而仅采用了均值计算，于是在文献[7]中同时提出了一种加权Slope One算法；Gao等人[8]将Slope One算法与基于内容的推荐算法结合起来，提高了推荐的准确性，但是在数据矩阵稀疏的情况下效果不理想，扩展性差；文献[9]研究表明，在用户评分矩阵稠密的时候Slope One算法相比于矩阵稀疏时有更好的推荐效果；Zhang等人[10]通过利用加权Slope One算法来填充稀疏矩阵，从而在最近邻集合中进行评分预测，相对缓解了矩阵稀疏的问题，提高了推荐准确性；Liu等人[11]利用项目相似性对稀疏矩阵填充，然后利用用户相似性进行最近邻寻找，有效缓解了矩阵稀疏性的问题；You等人[12]提出数据聚类的思想，减少了计算复杂度，在一定程度上提高了推荐算法的实时性。黄皓璇等人[13]将用户随着时间兴趣变化函数融入到Slope One算法中，提高了推荐的精度。

本文在前人研究的基础上，提出一种融合用户模糊聚类和用户相似度的加权Slope One算法，并通过实验将本文算法模型与传统的Slope One算法和加权Slope One算法进行对比，实验表明，本文算法进一步提高了推荐效率，降低了推荐误差。

1 相关工作

1.1 用户项目评分矩阵

通过对数据库中用户对项目的评价数据进行格式化，转化为m行n列的用户项目评价矩阵Ru,i,如表1所示，其中用户集U={u1,u2,…,um}由m个用户组成，项目集I={i1,i2,…,in}由n个项目组成，ri,j表示用户ui对项目ij的评分，若没有用户对项目评分则ri,j= 0，用户对项目的评分区间为1～5分，评分越高，代表用户对项目越喜欢。

表1 用户项目评分矩阵Ru,i

1.2 Slope One算法

Slope One是一种基于评分的协同过滤算法，于2005年由丹尼尔等人提出，具有易于实现、计算速度快、可扩展性好等特点，同时对数据稀疏性有较好的适应性；与其他的个性化推荐算法相比，Slope One算法无须计算项目之间的相似度,而是用一种简单的线性回归模型w=f(v)+b进行预测，其中，w代表目标用户对项目i的评分，f(v)代表目标用户对该项目以外的项目评分，b为项目i相对于其他项目(用j表示其他项目)的平均偏差，用Devi,j表示，如图1所示，有A用户和B用户2人，其中A用户对项目1和项目2都进行了评价，B用户仅对项目1进行了评价，通过以上条件来预测B用户对项目2的评分。利用Slope One算法可知B用户对项目2的评分为：2+(1.5-1)=2.5。

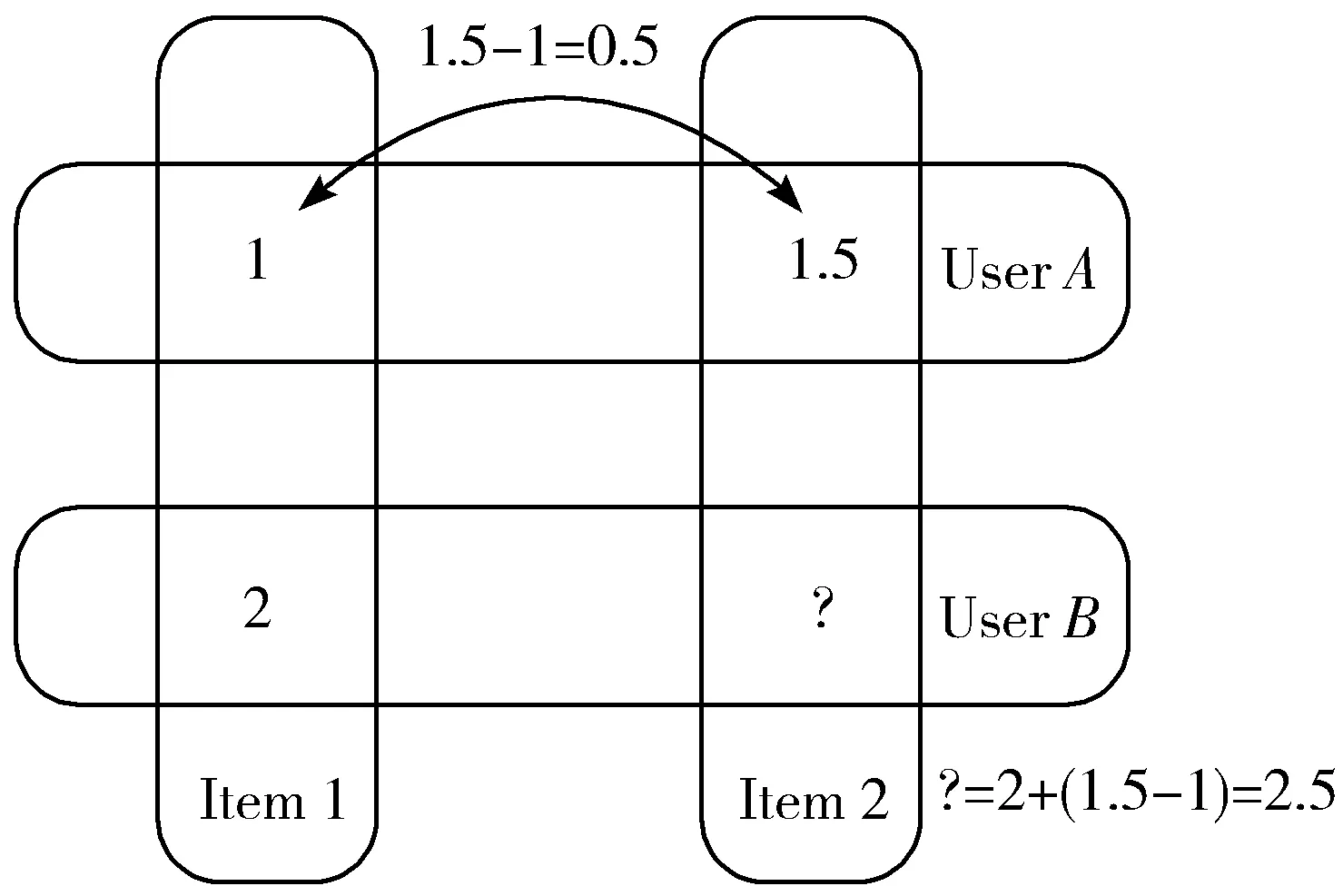
图1 Slope One算法的思想

用Devi,j表示目标项目与其他项目的平均评分偏差，计算公式如式(1)所示：

(1)

其中，x表示训练集,Si,j(x)表示对项目i以及其他项目(用j表示其他项目)都评分的用户集合，Num(Si,j(x))表示在Si,j(x)集合中的用户总数。

通过以上的分析以及在式(1)已知的基础上，利用Pu,i=Devi,j+ru,j即可通过式(2)计算出目标用户对目标项目的预测评分：

(2)

其中，ri表示目标用户对所有项目评分的集合，Num(ri)表示目标用户评分项目数量。

1.3 加权Slope One算法

在1.2节中的Slope One算法在计算2个项目的相对平均偏差Devi,j的时候，没有考虑到用户评价的项目数量而是进行了平均计算，缺乏合理性。例如一种情况为100人同时对项目i和项目j进行了评价，另一种情况为10人对项目j和项目k进行了评价，2种情形下得到的Devi,j和Devj,k有着不同的说服力。因此Lemire等人提出了Weighted Slope One算法，即加权Slope One算法，算法的思想是与目标商品共同评价的商品数量越多，给予更大的权值，该算法有效修正了评价偏差的计算，同时进一步提高了推荐的准确度，计算公式如式(3)所示：

(3)

其中，Pu,i代表用户u对项目i的评分预测，|Ci,j|为用户的数量权重。

1.4 模糊C-均值聚类

模糊C-均值聚类算法是一种基于划分的算法，不同于K-means等硬聚类算法，硬聚类算法可以导出确定的聚类，即一个对象仅能属于一个类，不存在重叠的情况。而模糊C-均值聚类的思想是一个对象在一定程度上属于一个类，也可以同时以不同程度属于几个类，因此模糊C-均值聚类是一种柔性的聚类算法。定义在论域D中任意一个元素x，如果都有一个U(x)∈[0,1]与x相互对应，则称U为D上的模糊集,U(x)称为x对D的隶属度。隶属度函数是表示一个对象x隶属于集合U的程度的函数，记为U(x)，取值范围为[0,1],函数值越趋近于1，则隶属度越高。

模糊C-均值聚类引入了模糊逻辑的概念，它用隶属度矩阵U=[uis]表示每个对象隶属于某个类的程度大小，模糊C-均值聚类的目标函数如式(4)所示：

(4)

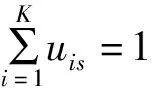
(5)

把上面的条件极值问题转化为无条件极值问题，引入n个拉格朗日因子，继而利用拉格朗日乘数法把条件极值转化为无条件极值问题，即可得到隶属度矩阵U,过程如下：

(6)

由式(6)可得：

(7)

(8)

(9)

将式(9)代入式(7)得uis，如式(10)所示,从而得到隶属度矩阵U：

(10)

聚类中心C的求解过程如下：

(11)

dist(ci,xs)2=‖ci-xs‖A=(ci-xs)TA(ci-xs)2

(12)

其中，A为权重，由式(11)和式(12)联立得式(13)：

即可得聚类中心ci如式(14)所示：

(14)

2 本文算法模型

本文对传统的加权Slope One算法按照如下步骤进行优化：

步骤1对用户项目评分数据集进行预处理,生成用户评分矩阵。

步骤2使用模糊C-均值聚类算法，对所有用户进行模糊聚类，将相似度高的用户划归同一类中。

步骤3在每个聚类内部根据用户评分矩阵计算用户间相似度并构建用户相似度矩阵，依据用户相似度矩阵寻找TopK个最近邻。

步骤4将用户相似度函数融入加权Slope One算法中，来计算项目间的偏差，并预测用户对项目的评分。

步骤5最后根据评分集合选择最优项目集推荐给目标用户。

2.1 对用户进行模糊C-均值聚类

聚类可以将有相似特征的用户进行快速的分门别类，同一聚类中的用户相似程度高，不同聚类之间的用户相似程度低。在构建完成用户簇后，可以根据同一类簇中用户的特征均值来评估目标用户。

当下处于大数据的时代，个性化推荐系统每天的数据以PB乃至TB量级的速度快速增长；当数据量越来越大，对系统的运算能力和效率产生了越来越大的挑战。因此，在对大量的数据进行计算前，先对数据进行聚类是提高系统效率、降低运算复杂度的有效方式。用户属性较多、特征多样，K-means算法[14]等一些硬聚类算法将用户硬性地分在一个簇中，缺乏合理性，而模糊C-均值聚类算法[15]是一种软聚类算法，可以利用数学理论定量地确定样本的亲疏关系，每个用户可以属于多个类簇，更加客观合理。

设N为用户集大小，K为聚类中心个数，UN×K={Us,i}为隶属度矩阵,C={c1,c2,…,ck}为聚类中心列表，式(15)为对用户模糊聚类的目标函数:

(15)

在协同过滤算法中，相似性的计算尤为重要，基于向量的相似性计算主要分为以下3种[16-21]:余弦相似度、修正的余弦相似度、皮尔逊相关系数。Herlocker等人[22]通过实验发现皮尔逊相关系数比其他相关性度量方法更加精确。因此，本文采用皮尔逊相似度的方法计算用户s和第i个聚类中心的相似度，计算公式如式(16)所示：

(16)

输入：用户向量表和终止条件簇的数目K;

输出：达到终止条件规定簇的数目，得到各类聚类中心和各个样本对于各类的隶属矩阵。

处理：

步骤1初始化各聚类中心；

步骤2Repeat；

步骤3根据式(17)用当前的聚类中心计算隶属度函数并更新隶属度矩阵U：

(17)

步骤4根据式(18)用当前的隶属度函数更新计算各聚类中心ci：

(18)

步骤5直到目标函数J(U,C)收敛，即完成了模糊聚类划分。

2.2 改进的加权Slope One算法

加权Slope One算法考虑了在计算项目间相对平均偏差过程中共同评分用户数量的权重因子，赋予共同评分用户数量多的项目以更大的权重值，虽然在部分情况下提高了推荐的精确度，但是在有些情况下也容易出现较大的误差，同时该算法也忽略了用户的相似度能对推荐结果产生影响的因素；因此，将用户的相似度函数融入到加权Slope One算法的偏差计算公式中进行优化，可以进一步地提高推荐的精确率。

计算用户或者项目间相似度常用的方法有杰卡德系数、余弦相似度和皮尔逊系数，其中皮尔逊系数去中心化和归一化的特性，即在用户对项目评分的基础上去掉所有用户对项目的平均评分，隐形地保留了用户评分的偏好特征，更能反映出用户间的线性相关性，因此在本次计算中，采用了皮尔逊相似度的计算方法来计算用户间的相似度，用数学公式表示，皮尔森相关系数为2个变量的协方差除以2个变量的标准差，如式(19)所示：

(19)

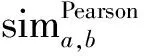
结合皮尔逊系数对加权Slope One算法的偏差计算公式进行改进，式(20)为改进后的加权Slope One算法中项目i和项目j的偏差计算公式Devi,j，最后通过式(3)即可求出预测评分值Pu,i，进而列出topN个得到最佳预测值的项目推荐给目标用户。

(20)

3 实验与结果分析

3.1 实验环境和数据集的选取

实验环境：macOS系统。硬件配置参数：CPU为2.3 GHz 4核Intel Core i5，内存为8 GB 2133 MHz，实验语言环境为Python3.7；实验数据集采用的是由明尼苏达大学的GroupLens团队采集并汇聚完成的电影评分数据集MovieLens。如表2所示，本文选用ml-100k数据包，它由943个用户创建，包含了对1682部电影的10万条评分数据，评分形式是采用1～5分来对电影进行打分，用户对电影的评分越高，表示当前用户对该电影越喜欢。

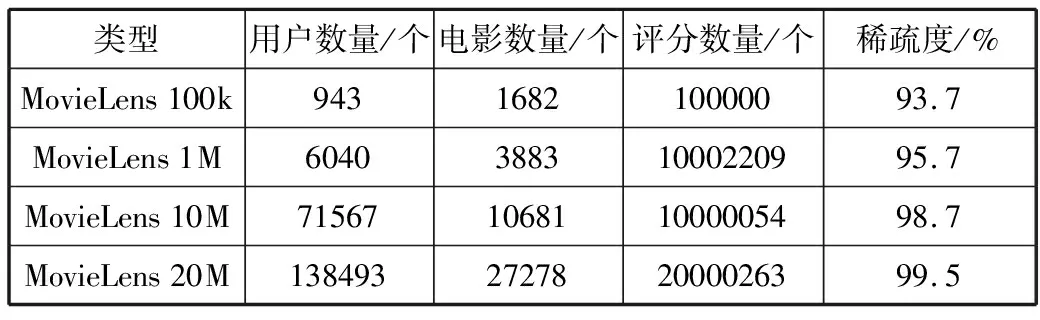
表2 MovieLens数据集

3.2 评价标准

在对本文算法模型进行标准评价中，采用平均绝对误差[23](Mean Absolute Error，MAE)来衡量推荐结果的有效性。平均绝对误差MAE是通过计算用户评分的预测值和用户评分的实际值之间的偏差平均值来度量算法是否精确。例如，有n个项目预测的评分向量为(p1,p2,…,pn),实际评分向量为(t1,t2,…,tn),则算法表示如式(21)所示：

(21)

3.3 结果对比与分析

设置实验1用来验证模型在不同聚类数量下的准确度情况，聚类簇数在[0,30]区间内，以间隔为4来观察聚类数量对实验的影响，结果如图2所示，在聚类簇数小于8时，MAE值呈下降状态，在聚类簇数为8的时候达到最佳，在大于8时，MAE值又呈现缓慢上升的趋势，说明在聚类数为8时,为本文算法模型的最佳状态。

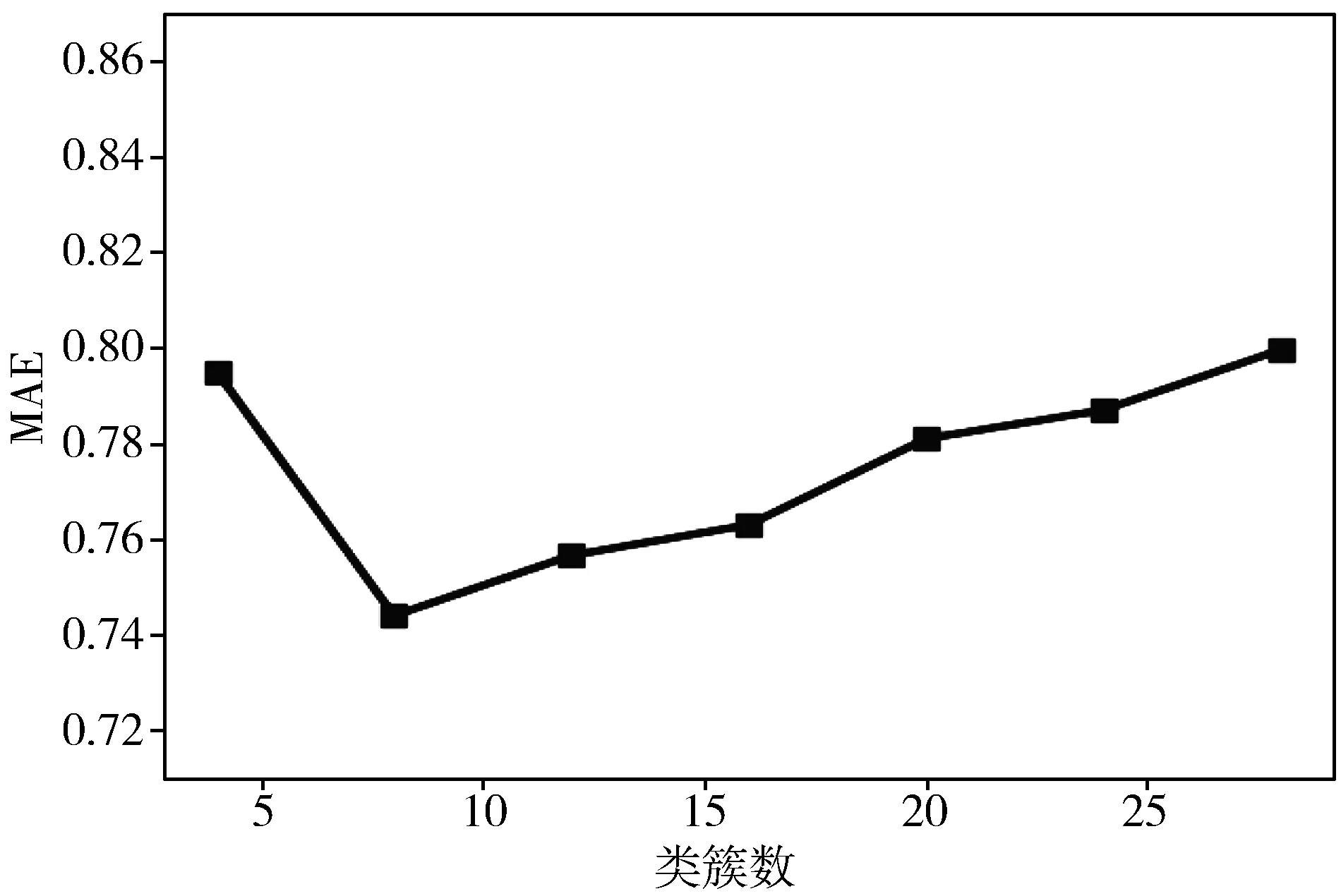
图2 不同聚类簇数下的MAE值

实验2在聚类数为8的情况下，将本文算法与传统的Slope One算法(SO)、基于聚类的Weighted Slope One算法、融合用户相似度的加权Slope One算法在不同数量的最近邻进行了对比实验，来验证本文算法模型的有效性和稳定性。从图3可以看出，随着最近邻居个数的逐渐增加，Slope One算法由于不受最近邻居的数量限制，所以其平均绝对误差不变，本文算法和Weighted Slope One算法及融合用户相似度的加权Slope One算法平均绝对误差呈现下降的趋势，然后又逐步趋近平缓状态。说明最近邻居并非越多越好，而是在达到最佳数量后，数量对最小平均误差影响权重变小。

经过实验以及与其他算法的对比，验证了本文算法的有效性和稳定性。最终通过图4可了解到本文算法确实改进了推荐效果，在一定程度上较以往算法在推荐精确度上得到有效提升。

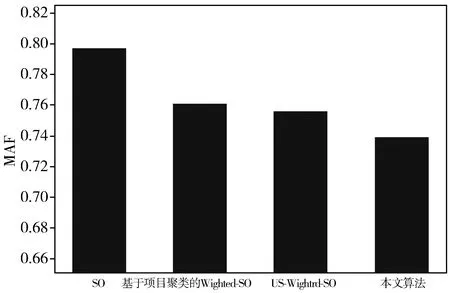
图4 本文算法与其他算法MAE对比

4 结束语

本文通过分析传统的Slope One算法的思想和缺陷，以及对学者关于这一研究做出了一些突破和成就进行了叙述和参考，针对传统Slope One算法在预测和推荐中的准确度和稳定性进行了进一步的优化，首先引用模糊聚类算法对巨大复杂的用户集中相似的用户进行了聚类；同时对传统的加权Slope One算法进行了改进，将用户相似度融合进Weighted Slope One算法中，然后进行评分预测并寻找最优推荐项目集合，最后通过实验将本文算法模型与其他3种经典算法模型进行了对比和分析，验证了本文算法模型在一定程度上提高了推荐效率，对推荐结果的精准性和有效性起到了积极作用。