基于变权优化背景值改进的GM(1,1)灰色预测模型及其应用
张丽洁,沙秀艳,尹传存,段钧陶,张欣怡,李紫桐,姜福蕾
(曲阜师范大学统计学院,山东 济宁 273165)
0 引 言
灰色系统理论由邓聚龙教授[1]在1982年首先提出,是一种研究少数据、贫信息不确定性问题的新方法。GM(1,1)模型是灰色系统理论中最基础也是应用最广泛的模型,其建模原理简单[2],即将灰色数列进行累加或累减得到新的生成数列,建立灰色预测微分方程模型,对原始数列进行模拟,并对未来进行预测。小样本、贫信息不确定性系统的大量存在使得GM(1,1)模型具有十分宽广的应用领域,目前已广泛应用于工业、社会、经济、科技等领域的预测和评估[3-8]。但这并不意味着其可以随意应用,刘思峰等[9]研究了GM(1,1)模型的适用范围,确定其有效区、慎用区、不宜区和禁区;李峥[10]对GM(1,1)模型的背景值进行分析,指出其存在取法固定、缺乏灵活性和易受原始数据影响造成结果失真的问题;何海等[11]也指出GM(1,1)模型预测公式系数的选取存在缺陷。
为解决传统的GM(1,1)模型拟合预测精度不高的情况,各学者相继从背景值优化、微分方程优化、初始值优化等方面给出了改进模型。对于背景值优化,田梓辰等[12]利用拉格朗日插值与改进的拉格朗日插值函数分别对灰色GM(1,1)模型进行了背景值的重构;唐万梅等[13]提出用二次插值构造模型中的背景值,同时用最小二乘法对预测公式中的初值进行改进。对于微分方程优化,陈鹏宇等[14]从白化方程与灰微分方程的匹配问题出发,提出白化方程参数重构法。对于初始值优化,吴文泽等[15]从修正初始值的角度出发,提出“新信息优先使用”的初始值选取原则;谢锦彪等[16]提出基于最小二乘法原理改进模型初始值参数的选取策略。
本文先阐述传统的GM(1,1)模型的基本原理[17],然后提出基于优化背景值和建立递推方程相结合的改进模型。首先运用黄金分割搜索与抛物线插值法相结合确定改进GM(1,1)模型的背景值,并用灰色预测代数递推方程代替传统的GM(1,1)模型中的微分方程或白化方程,将改进后的背景值代入灰色预测代数递推方程。最后对非齐次指数方程产生的随机序列进行模拟检验,再根据某高校教师人数的实际统计数据,分别对传统的GM(1,1)模型与改进的GM(1,1)模型进行仿真实验。结果表明,改进后的模型预测精度显著提高,有效性和可行性更好。
1 传统的GM(1,1)灰色预测模型
传统的GM(1,1)灰色预测模型是用原始数据组成原始数据序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)},经过累加生成X(1)={x(1)(1),x(1)(2),…,x(1)(n)},弱化原始数据的随机性,使其呈现出较为明显的特征规律。对生成变换后的序列X(1)建立一阶微分方程,再对微分方程求解并将所求结果再累减还原得到灰色预测值,从而实现对未来数据进行预测[18]。具体过程如下:
步骤1设X(0)={x(0)(1),x(0)(2),…,x(0)(n)}为GM(1,1)模型的原始序列,对其一次累加得公式:
X(1)={x(1)(1),x(1)(2),…,x(1)(n)}
(1)
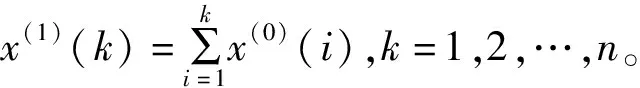
令z(1)为x(1)的均值序列:
z(1)=(z(1)(2),z(1)(3),…,z(1)(n))
(2)

步骤2建立GM(1,1)模型的灰微分方程:
x(0)(k)+az(1)(k)=u
(3)
相应的白化微分方程为:
(4)
步骤3利用最小二乘法,对灰微分方程进行参数估计,求发展系数a和灰色作用量u,得:
其中:
(5)
步骤4求解方程得:
(6)
步骤5由于GM(1,1)模型得到的是一次累加量,须将所得数据经过逆生成还原,根据还原公式:
(7)
可对原始数列进行拟合和预测。
2 改进的GM(1,1)灰色预测模型
传统的GM(1,1)模型作为灰色预测的核心和基础,在各领域得到了广泛的应用。然而,其背景值系数固定,缺乏灵活性,使模型易出现预测结果失真的问题。对此,本文提出基于黄金分割搜索和抛物线插值法相结合的变权优化的背景值系数,同时,建立灰色预测递推方程代替传统的白化方程,使模型的预测结果具有一定的平滑性,避免了原始预测模型验证失真的问题,将改进的背景值代入方程,得到改进后的GM(1,1)模型。
2.1 背景值的改进

步骤1假设函数f(α)为相对误差曲线,依据黄金分割比例在区间[0,1]产生一个初始迭代点,即αi。
步骤2利用黄金分割搜索得到新的迭代点αi+1,具体见图1所示。比较f(αi)与f(αi+1)的大小,若二者相差不大(满足黄金分割法精度要求),则转向步骤3,用抛物线插值法迭代一步。否则,由图1可知,若fi+1=f(i+1)a,则新区间为[α1,αi,αi+1],若fi=f(i+1)b,则新区间为[αi,αi+1,α2],令i=i+1,重复步骤2进行迭代。

图1 黄金分割比例图
步骤3函数f(α)在α1,α2,α3点处的值分别为f(α1),f(α2),f(α3)。
用抛物线φ(α)=a0+a1α+a2α2拟合f(α),即φ(αi)=f(αi),i=1,2,3。
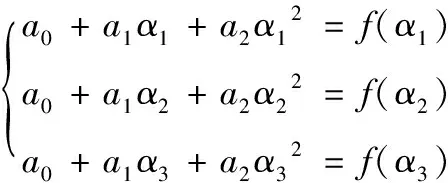
设α为φ(α)极小值点,令φ′(α)=0,解得:
(8)
利用克莱姆法则解上述方程组并代入式(8)可得:
(9)
步骤4若f(α)与黄金分割搜索得到的相对误差值相差不大,则再用抛物线插值法进行一次迭代,如果连续2次抛物线插值法得到的f(α)及自变量α值相差不大,则继续迭代直到满足精度要求,否则重复步骤2。
利用上述步骤,求得预测相对误差最小值时的对应点α后,将α代入改进的背景值公式[21]:
z(1)(k)=αx(1)(k)+(1-α)x(1)(k-1)
(10)
为了更清晰地表明传统的GM(1,1)模型的背景值与改进的GM(1,1)模型的背景值的不同,本文给出其流程对比图,详见图2。

图2 背景值流程对比
2.2 构造灰色预测迭代方程
针对传统的GM(1,1)模型预测精度不高的缺点,文献[22]将传统的GM(1,1)模型的一次累加公式改写为:
(11)
进而结合式(3),得到:
(12)
即:
(13)
令:
(14)
由式(13)可得到灰色预测迭代方程[22]:
(15)
其中,当nk时为模型拟合值;当n>k时为模型预测值。根据式(5)和式(14)求得a、u、b,并代入式(15)得到预测结果。该模型的预测结果一定程度上增强了预测模型的平滑性。
2.3 改进的GM(1,1)灰色预测模型的实现过程
2.2节中文献[22]的方法虽然在一定程度上提高了模型的平滑性,但未能克服传统的GM(1,1)模型具有均等权值导致预测精度不高的缺点。因此本文提出一种基于变权优化选择背景值和建立灰色递推方程相结合的改进GM(1,1)灰色预测模型。具体步骤如下:
步骤1利用2.1节黄金分割搜索和抛物线插值法相结合确定背景值权值α的数值。
步骤2将α代入背景值公式。
z(1)(k)=αx(1)(k)+(1-α)x(1)(k-1)
(16)
步骤3计算灰色预测迭代方程。
由传统的GM(1,1)模型的灰微分方程(3)可得:
x(0)(k)+a(αx(1)(k)+(1-α)x(1)(k-1))=u
(17)
即:
(1+aα)x(0)(k)+ax(1)(k-1)=u
(18)
令c=1+aα,将式(18)变形为:
(19)
式(19)与x(1)(k-1)=x(1)(k-2)+x(0)(n-1)联立,可得:

(20)
以此类推,最终得到灰色预测迭代方程:
(21)
其中,当nk时为模型拟合值;当n>k时为模型预测值。
步骤4利用式(5)求得a、u,进而求得c,将三者代入式(21)可得到最终的预测结果。
为了更清晰地表明改进的GM(1,1)灰色预测模型的具体实现过程,本文给出改进模型的流程图,详见图3。

图3 改进的GM(1,1)灰色预测模型的流程图
3 应用实例
为了验证本文提出的GM(1,1)灰色预测模型改进算法的有效性和可行性,这里选用文献[15]与文献[23]中的数据分别进行实例检验,检验结果如下。
实验1文献[15]中取用的原始数据x(0)(k)={2.98,4.45,6.64,9.90,14.77,22.04,32.88}为一低增长指数数列,对其分别利用传统的GM(1,1)灰色预测模型和本文改进的模型进行对比分析,具体结果如下。
根据2.1节中的方法,利用MATLAB R2018b编程[24],运用黄金分割搜索结合抛物线插值法在[0,1]区间内搜索得到灰色预测相对误差与背景值权值α的关系迭代曲线图,如图4所示。
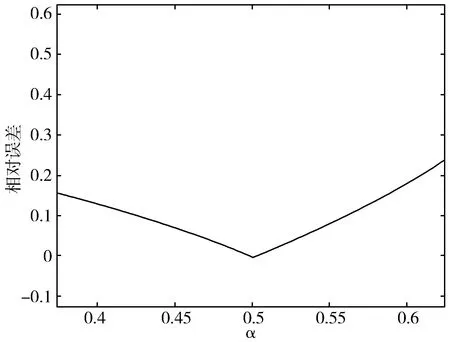
图4 实验1的相对误差
针对不同的α值代入背景值后,得到改进后模型不断迭代优化的预测结果,详见图5。

图5 实验1的迭代优化过程
根据图4可以得到预测相对误差最小值时对应的α值,代入背景值后,得到改进后GM(1,1)灰色预测模型最终的预测结果并对其进行误差分析,详见表1、图6和图7。

图6 实验1的2种模型的预测结果
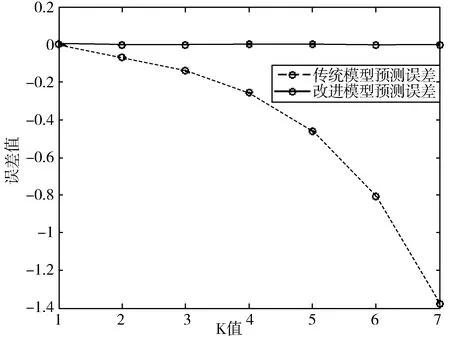
图7 实验1的2种模型预测结果与实际值的误差比较
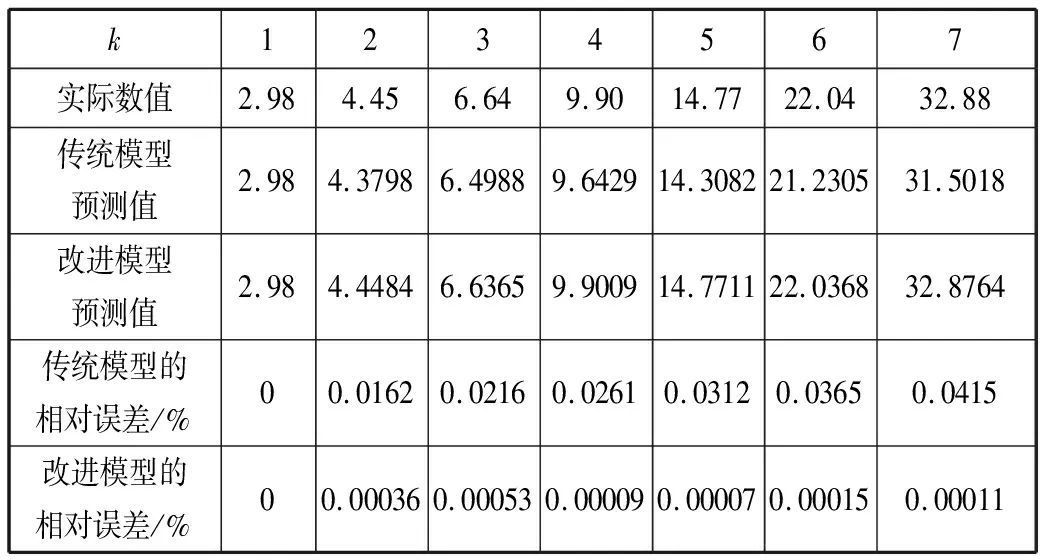
表1 实验1的2种模型的预测结果
由表1和图6可以看出,改进的GM(1,1)灰色预测模型模拟精度更高,相对误差更小,也就意味着改进的GM(1,1)模型的预测性能是优于传统的GM(1,1)模型的。
图7展示了2种模型的误差比较,不难看出,改进的GM(1,1)模型的误差在0附近上下浮动且浮动范围较小,而传统的GM(1,1)模型的误差越来越大,这表明改进后的模型预测精度更高,预测性能更好。
为了更好地比较传统的GM(1,1)灰色预测模型和本文改进的模型的性能,本文针对2种模型分别进行了方差比检验、小误差概率检验、平均相对误差检验。具体比较结果见表2。

表2 实验1的2种模型的检验结果
1)方差比检验。
原始数据标准差:
预测数据标准差:
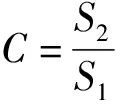
2)小误差概率检验。
小误差概率公式:
3)相对误差。

通过表2可以看出,改进的GM(1,1)灰色预测模型的各检验结果均优于传统的GM(1,1)模型,改进的GM(1,1)模型对真实数据拟合程度更高。
实验2文献[23]中取自河北省某高校1999—2003年教师人数的真实数据(详见表3),分别利用传统的GM(1,1)灰色预测模型和本文改进的模型进行对比分析,具体结果如下。
根据2.1节中的方法运行程序,得到灰色预测相对误差与背景值权值α的关系迭代曲线图,如图8所示。

图8 实验2的相对误差
针对不同的α值代入背景值后,可以得到改进后模型不断迭代优化的预测结果,详见图9。
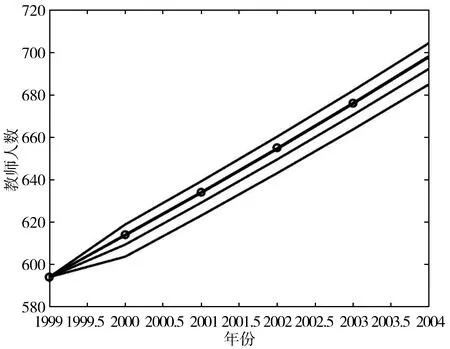
图9 实验2的迭代优化过程
从图8可以得到预测相对误差最小值时对应的α值,代入背景值后,可以得到改进后GM(1,1)灰色预测模型最终的预测结果,详见表3、图10和图11。

图10 实验2的2种模型的预测结果

图11 实验2的2种模型预测结果与实际值的预测误差比较
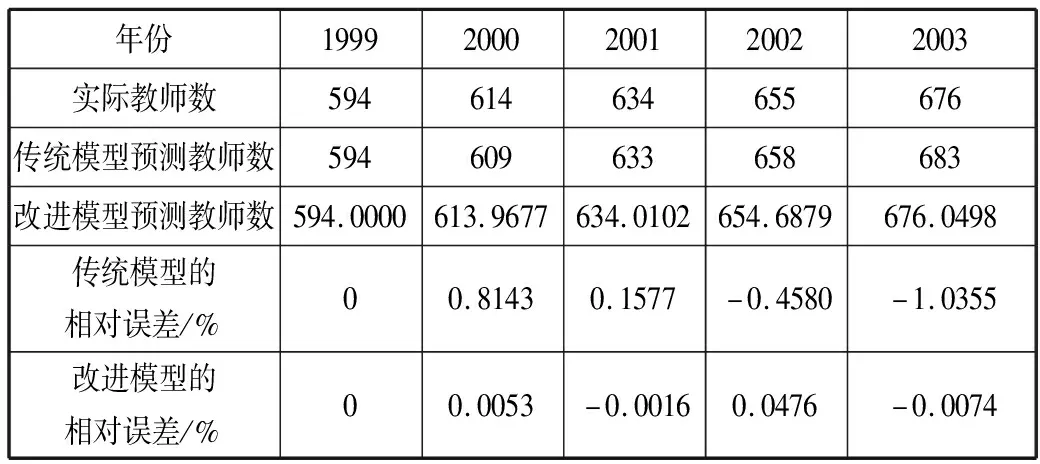
表3 实验2的2种模型的预测结果
从表3和图10可以看出,改进的GM(1,1)灰色预测模型比传统的GM(1,1)灰色预测模型预测结果更为精确,降低了相对误差。这是因为本文通过采用黄金分割搜索结合抛物线插值法,找到预测相对误差达到最小对应的背景值后,进而得到最终较好的预测结果。
图11展示了2种模型预测结果的误差比较,结果表明,传统的GM(1,1)模型误差波动较大,而改进的GM(1,1)模型误差较为平缓,且传统的GM(1,1)模型的误差始终高于改进的GM(1,1)模型的误差,即改进后的模型有效减小了误差,预测性能更好。
接下来对2种模型进行性能检验,具体检验结果见表4。
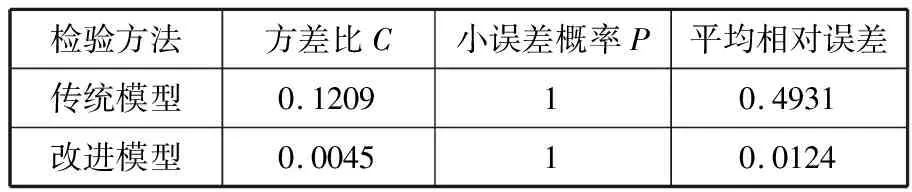
表4 实验2的2种模型的检验结果
通过表4可以看出,改进的GM(1,1)灰色预测模型比传统的GM(1,1)灰色预测模型预测方差比和平均相对误差更小,预测结果更为精确,对真实数据拟合程度更高。
综上所述,改进的GM(1,1)模型的精度远高于传统的GM(1,1)模型的精度,有效提高了模拟精度和预测精度,具有较好的预测性能。
4 结束语
自灰色系统理论创建以来,经过30多年不断的完善和发展,已经在许多领域得到了广泛应用。本文在研究传统的GM(1,1)灰色预测模型的基础上,提出了一种变权优化背景值结合递推方程的改进的GM(1,1)灰色预测模型。在背景值优化方面,结合实际统计数据运用黄金分割搜索和抛物线插值法构造权值确定背景值。在白化方程方面,建立灰色预测递推方程代替传统的白化方程并代入改进的背景值,得到了优化后的GM(1,1)模型。最后利用指数序列和真实的统计数据,分别对传统的GM(1,1)灰色预测模型和改进的GM(1,1)灰色预测模型进行仿真实验,结果表明,本文提出的模型预测精度更高,可行性和可靠性更好,具有一定的实际意义和应用前景。

