RV 减速器传动系统动力学特性分析
庞 杰,韩振南
(太原理工大学机械工程学院,山西 太原 030024)
1 引言
自20 世纪80 年代以来,学者们对RV 传动的研究有了很大的进展[1-2],主要以RV 传动精度及动态性能为主。文献[3]建立了双曲柄轴RV 减速器扭转动力学模型,简化模型并对整机扭转刚度进行分析。文献[4]建立了考虑摆线轮与曲柄轴公转运动的双曲柄轴RV 减速器扭转动力学模型,计算了整机固有频率及其对系统的灵敏度。文献[5]建立了三曲柄轴RV 减速器平移-扭转动力学模型,分析了整机固有特性。这些模型只考虑了定刚度和阻尼对整个系统的影响,缺少对传动过程中啮合阻尼、时变啮合刚度、综合传动误差的考虑。以三曲柄轴RV 传动系统为例,建立了考虑轴承支承刚度、齿轮副啮合阻尼、时变啮合刚度及综合啮合误差的RV 传动纯扭转动力学模型,运用数值解法求解,得到了RV传动系统的振动响应,为RV 减速器的优化设计奠定基础。
2 RV 减速器传动原理
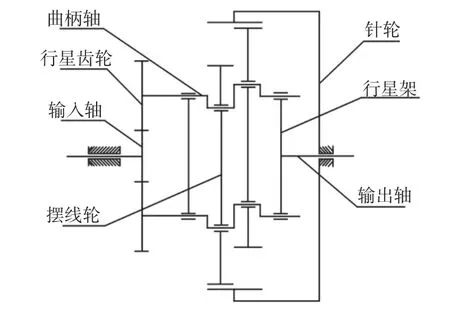
图1 RV 减速器传动机构简图Fig.1 Schematic Diagram of the RV Reducer Drive Mechanism
RV 传动系统机构简图,如图1 所示。动力由电机输入,与输入轴相连,通过与渐开线行星齿轮啮合,实现第一级减速;行星轮与曲柄轴固接,作为摆线针轮传动的输入部分,通过曲柄轴带动摆线轮与固定针轮啮合,摆线轮公转的同时,将摆线轮的自转运动通过行星架输出。
3 RV 传动系统动力学模型的建立
3.1 动力学模型的建立
采用动态子结构法与集中参数法建立RV 传动系统动力学模型。但RV 减速器的运动比较复杂,故对RV 传动系统进行以下简化:(1)转臂轴承与角接触支承轴承简化为弹簧;(2)设三个行星齿轮的质量、转动惯量、轮齿啮合刚度完全相同;(3)设转臂轴承与角接触球轴承的支承刚度是恒定的;(4)忽略齿面啮合摩擦力的影响假设轮齿啮合力始终沿啮合线方向;(5)曲柄轴上轴承间距小,忽略其弯曲变形;(6)将输入齿轮轴分为输入轴与第一级渐开线齿轮传动主动齿轮两个集中质量模型;(7)将曲柄轴简化为三个集中质量点,分别为渐开线齿轮传动中心,以及支承摆线轮回转运动的两处中心;(8)曲柄轴第一集中质量点与行星齿轮固接成一个集中质量点。RV 传动系统集中参数动力学模型,如图2 所示。
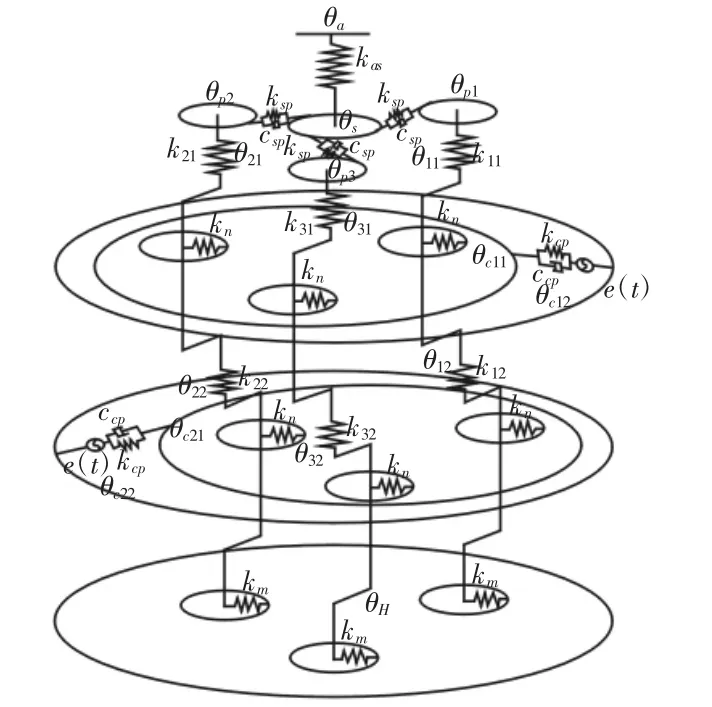
图2 RV 减速器动力学模型Fig.2 Dynamics Model of RV Reducer
以输入轴中心为原点,输入轴轴线方向为z 轴,以中心指向第一个曲柄轴轴线方向为y 轴,建立笛卡尔坐标系。通过上述建立的动力学模型得到动力学方程为:
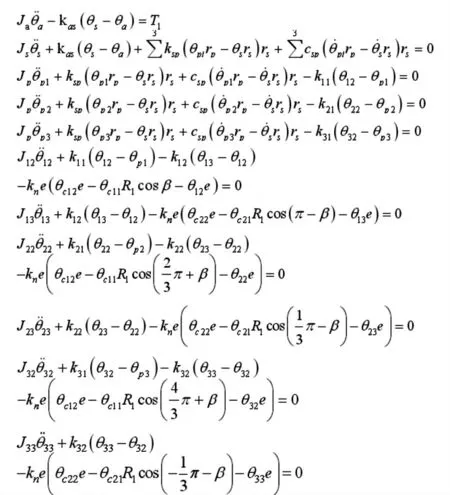
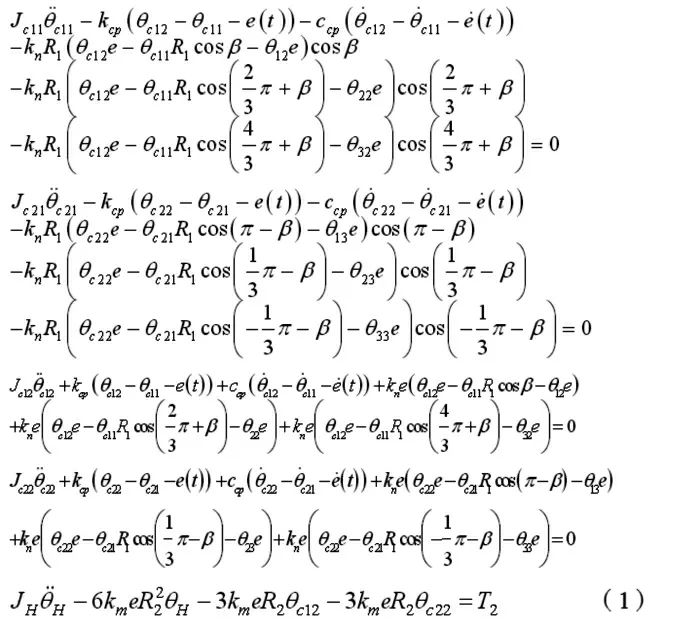
式中:Ja、Js、Jp、JH—输入轴、渐开线齿轮传动太阳轮、渐开线齿轮传动从动齿轮、行星架惯性矩;θa、θs、θpi、θH—输入轴、渐开线齿轮传动太阳轮、渐开线齿轮传动从动齿轮、行星架振动角位移;Jij—第 i 个曲柄轴第 j 个集中质量惯性矩;θij—第 i 个曲柄轴第 j 个集中质量振动角位移,i 取 1,2,3,j 为 1,2;Jc11—摆线轮1 自转惯性矩,θc11—摆线轮自转振动角位移;Jc12—摆线轮1 公转惯性矩,θc12—摆线轮1 公转振动角位移;Jc21—摆线轮2 自转惯性矩,θc21—摆线轮2 自转振动角位移;Jc22—摆线轮2 公转惯性矩;θc22—摆线轮2 公转振动角位移;kas—输入轴扭转刚度;ksp、csp—渐开线齿轮啮合刚度与啮合阻尼;kij—第i 个曲柄轴第j 段扭转刚度;kn—转臂轴承支承刚度;kcp、ccp—摆线针轮传动扭转刚度与扭转阻尼;e(t)—摆线针轮传动综合啮合误差;km—支承轴承支承刚度;R1—转臂轴承中心分布圆半径;R2—支承轴承分布圆半径;β—曲柄轴两个偏心轴线所在平面与过曲柄轴中心线和摆线轮中心轴线所成平面的夹角。
3.2 时变啮合刚度
3.2.1 渐开线齿轮传动时变啮合刚度
根据石川公式计算单对齿啮合刚度与双对齿啮合刚度,进而求得渐开线齿轮平均啮合刚度,用傅里叶级数表示渐开线齿轮时变啮合刚度为:

式中:km—平均啮合刚度;k1—刚度幅值;ωsp—啮合角频率,ωsp=2πnz/60;φ—啮合相位角。
3.2.2 摆线针轮传动时变啮合刚度
由于摆线针轮传动在传动过程中啮合齿对数多,不能简单将摆线轮齿与针齿啮合的法向啮合刚度叠加,因此,将其转化为扭转刚度模型进行计算[6],则得到摆线轮齿与针齿啮合的扭转接触刚度为:

式中:li—第i 对摆线轮齿与针齿接触力作用力臂;n—接触齿对数;kni—单对齿啮合刚度。
3.3 啮合阻尼
渐开线齿轮副啮合阻尼[7]按以下公式计算:

式中:ξ—齿轮啮合阻尼比,一般取(0.03~0.17);ksp—渐开线齿轮传动平均啮合刚度;Js,rs—太阳轮转动惯量与基圆半径;Jp,rp—行星齿轮转动惯量与基圆半径。
摆线针轮传动扭转阻尼为:

式中:kcp—摆线针轮传动扭转啮合刚度;Jc,rc—摆线轮转动惯量与基圆半径;Jz,rz—针轮转动惯量与基圆半径。
3.4 综合传动误差
因渐开线齿轮传动部分的误差较摆线针轮传动部分的误差对RV 传动误差的影响小得多,故不计渐开线齿轮传动部分的误差,只考虑摆线针轮传动部分的传动误差。
摆线针轮传动部分的传动误差简化为正弦曲线为:

式中:E—传动误差均值;ω—啮合角频率。
摆线针轮传动部分的传动误差包括在曲柄轴转一圈(摆线轮转一个齿)与输出轴转一圈的过程中,两部分的转角误差,前者称为小周期的传动误差,后者称为大周期的传动误差[8]。摆线针轮传动小周期传动误差,如表1 所示。摆线针轮传动大周期传动误差,如表2 所示。

表1 摆线针轮传动小周期传动误差Tab.1 Small Period Transmission Error of Cycloid Drive

表2 摆线针轮传动大周期传动误差Tab.2 Large Period Transmission Error of Cycloid Drive
4 RV 减速器仿真求解
采用(4~5)阶变步长 Runge-Kutta 法对 RV 传统系统动力学方程进行数值积分方法求解。输入参数如下:额定功率1.64kW,输入转速为1515r/min,得到RV 传动系统在内部激励与外部激励下各部分的振动位移和振动速度。RV 减速器各构件参数,如表3 所示。各部分支承刚度及扭转刚度,如表4 所示。
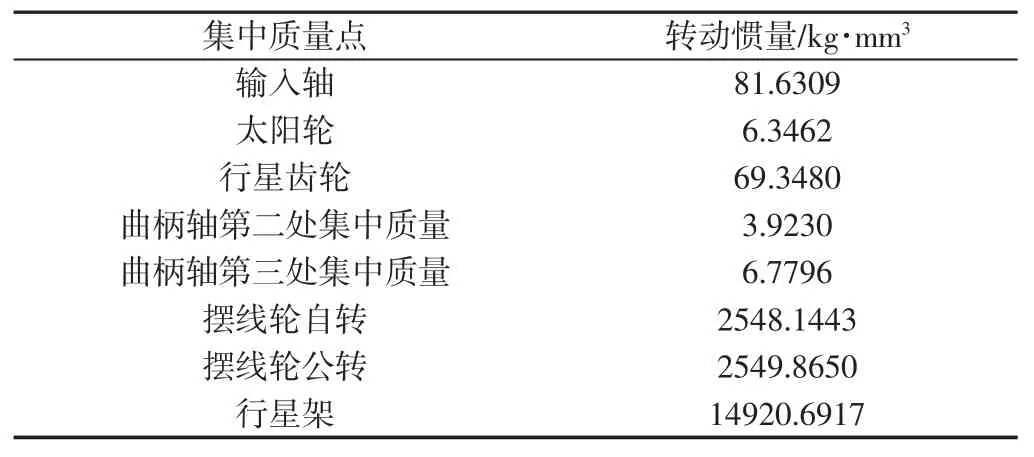
表3 RV 减速器各构件参数Tab.3 Components Parameters of RV Reducer

表4 各部分支承刚度及扭转刚度Tab.4 Support Stiffness and Torsional Stiffness of Each Part
4.1 振动角位移分析
传动系统主要传动部分的振动位移响应,如图3 所示。其中,太阳轮振动角位移曲线,如图3(a)所示。行星轮振动角位移曲线,如图3(b)所示。行星架振动角位移曲线,如图3(c)所示。太阳轮振动角位移幅值为0.1094°,平均值为0.0256°;行星轮振动角位移幅值为0.1097°,平均值为0.0280°;行星架振动角位移幅值为0.1092°,平均值为0.0240°。比较各构件的振动角位移,表明高速级行星轮的振动位移大,低速级行星架的振动位移最小。


图3 各部分振动角位移Fig.3 Vibration Angular Displacement of Each Part
4.2 振动角速度分析
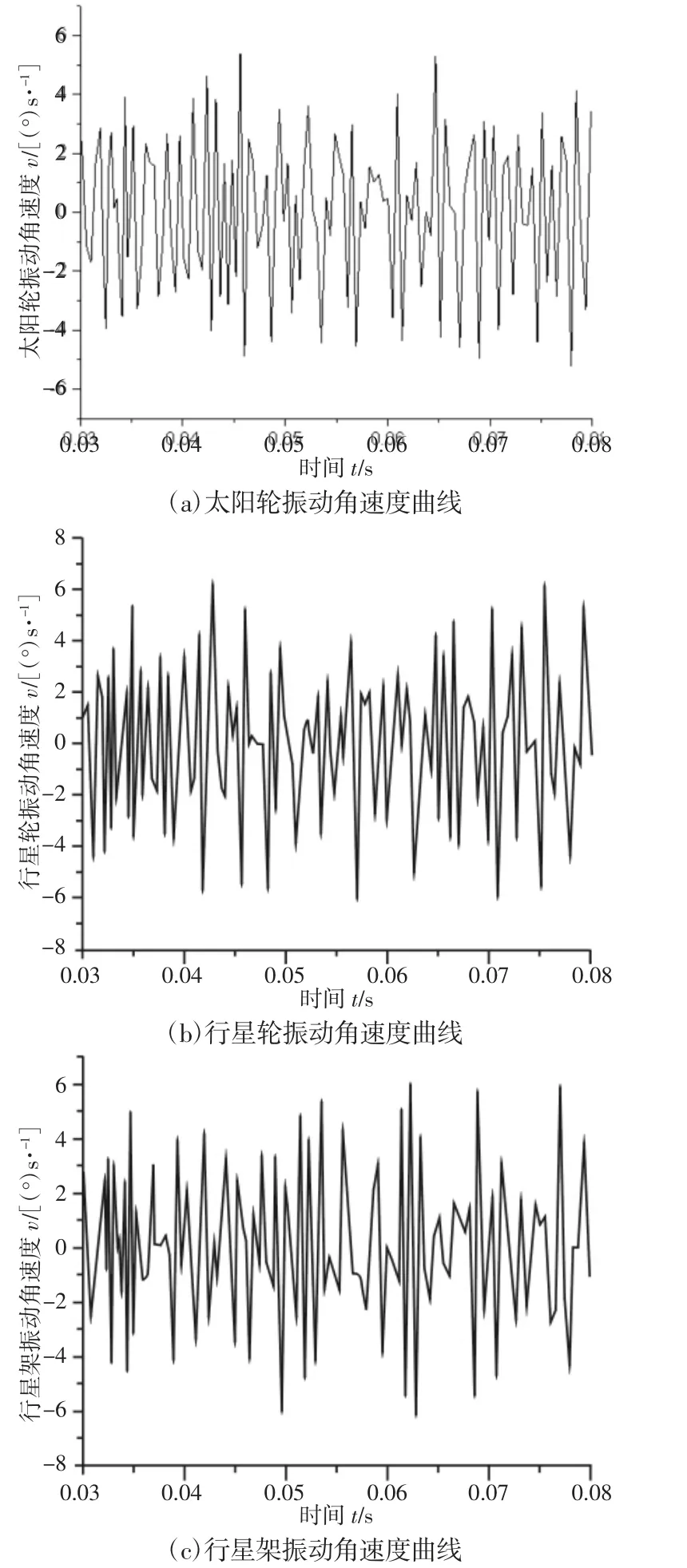
图4 各部分振动角速度Fig.4 Vibration Angular Velocity of Each Part
传动系统主要传动部分的振动速度曲线,如图4 所示。其中,太阳轮振动角速度曲线,如图4(a)所示。行星轮振动角速度曲线,如图4(b)所示。行星架振动角速度曲线,如图4(c)所示。太阳轮振动角速度幅值为5.3825°/s;行星轮振动角速度幅值为6.2832°/s;行星架振动角速度幅值为5.9364°/s。比较各传动部分振动角速度,系统各部分扭转振动角速度以零为中心上下波动,高速级行星轮振动较为剧烈。
5 ADAMS 仿真验证分析
在UG 中建立RV 减速器实体模型,导入到ADAMS 中进行动力学仿真[9-10]。输出行星架振动角速度仿真时域曲线;数值仿真结果中,行星架振动角速度均值为0.014°/s,ADAMS 仿真结果中,行星架角速度均值为0.012°/s,如图5 所示。根据RV 减速器传动技术要求,其输出误差小于1′/s,即0.017°/s。比较仿真结果,输出振动角速度曲线相差极小,验证数值仿真是准确的。
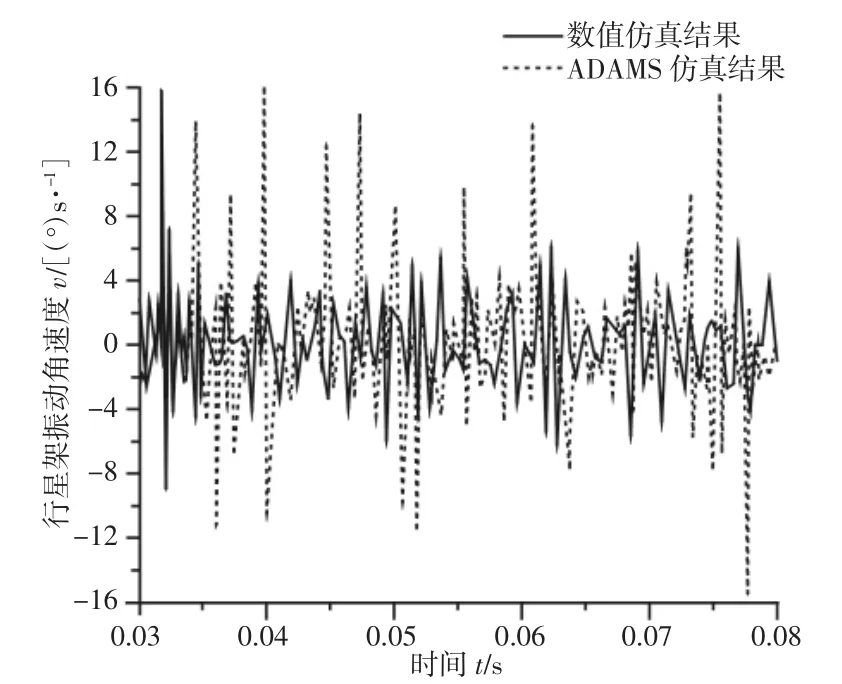
图5 输出角速度对比分析Fig.5 Comparison Analysis of Output Angular Velocity
5.1 啮合力验证分析
根据动力学模型分析,对渐开线齿轮传动中啮合线方向的线位移为:

则渐开线齿轮传动啮合力为:

对摆线针轮传动过程中,其扭转角位移为:

则摆线针轮传动等效扭转力矩为:
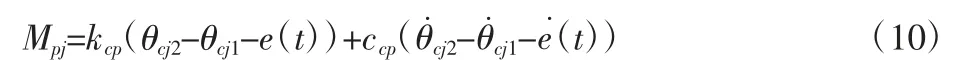
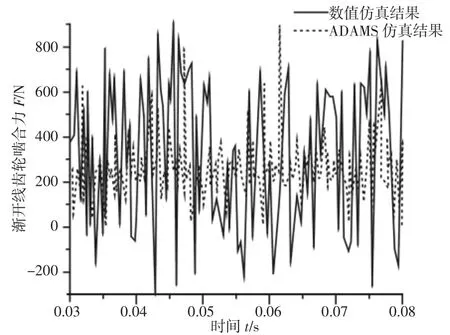
图6 渐开线齿轮传动啮合力对比分析Fig.6 Comparison Analysis of Meshing Force of Involute Gear Drive
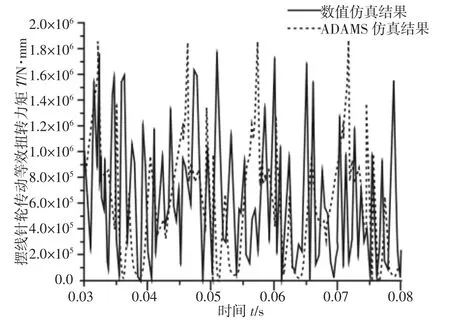
图7 摆线针轮传动等效扭转力矩对比分析Fig.7 Comparison Analysis of Equivalent Torsion Torque of Cycloid Drive
通过数值仿真求解与ADAMS 仿真对RV 减速器进行动力学分析。渐开线齿轮传动啮合力,如图6 所示。摆线针轮扭转力矩,如图7 所示。其具有相同的振动特征,数值仿真结果中,渐开线传动啮合力均值为233.5N;ADAMS 仿真结果中,啮合力均值为242.49N,误差小于6%;数值仿真结果中,摆线针轮扭转力矩均值为640053N/mm,ADAMS 仿真结果中,扭转力矩均值为5977-91.2N/mm,误差小于7%。分析表明,低速级摆线针轮传动动态啮合力较大,高速级行星齿轮传动动态啮合力较小。
5.2 啮合刚度对啮合力的影响
为深入研究RV 传动系统的动态特性,啮合刚度是影响齿轮传动系统动态特性的重要因素。渐开线齿轮传动直接影响整个RV 传动的动态特性,因此,通过改变渐开线齿轮传动时变啮合刚度来探究啮合刚度对动态啮合力影响。
渐开线齿轮传动啮合力随啮合刚度变化曲线,如图8 所示。从曲线图可得,随着啮合刚度的增大,啮合力的变化更加剧烈。因啮合刚度增加,啮合过程中内部激励增加,使得啮合力变化较大。
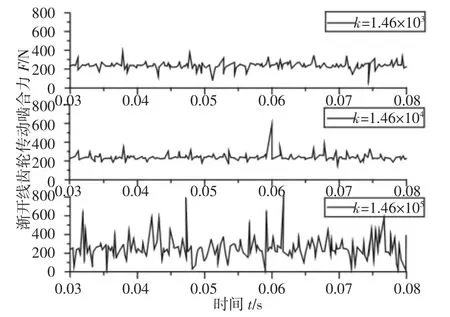
图8 渐开线齿轮传动啮合力随刚度变化曲线Fig.8 Variation Curve of Meshing Force with Stiffness of Involute Gear Transmission

表5 啮合力变化幅值与均值Tab.5 Amplitude and Mean of Meshing Force Change
啮合力变化幅值与均值,啮合力变化幅值增大,啮合力均值逐渐减小,因啮合变形减小,齿轮传动过程中最接近理想状态,如表5 所示;当刚度达到一定值时,啮合力不再保持同样的振动特征。啮合刚度达到一定值时的啮合力曲线,如图9 所示。

图9 刚度为1.46×106 时啮合力曲线Fig.9 Meshing Force Curve When Stiffness is 1.46×106
6 结论
(1)以三曲柄轴RV 传动系统为研究对象,综合考虑轴承支承刚度、啮合阻尼、时变啮合刚度,并考虑摆线针轮传动过程中的小周期与大周期传动误差,建立RV 传动系统扭转动力学模型。(2)对动力学模型进行数值积分求解,得到RV 传动系统角位移振动响应、角速度振动响应,各级传动啮合力响应。并通过ADAMS 仿真验证,输出误差<1′/s,渐开线齿轮传动啮合力误差<6%,摆线针轮传动等效扭转力矩误差<7%,因啮合刚度、啮合阻尼、传动误差与实际运动过程中有细微差距,故求解结果存在微小误差。(3)通过改变啮合刚度,得到其对RV 传动系统动态特性的影响,随着啮合刚度的增加,在一定范围内,传动过程中的啮合力更加稳定。当啮合刚度>1.46e6N·mm-1时,啮合力急剧增加,不再收敛,因此,需合理考虑齿轮传动过程中啮合刚度。

