考虑可靠度和可用度的民机维修间隔优化研究

李景奎，蔺瑞管，段飞飞，王俊辉

（1.沈阳航空航天大学民用航空学院，辽宁 沈阳 110136；2.中国南方航空股份有限公司沈阳飞机维修基地，辽宁 沈阳 110136）

1 引言

民机维修经历了从事后维修到预防性维修的发展阶段，预防性维修由于具有提高设备可用性和减少维修费用等优点，在民机维修中占有重要的地位[1]。目前，我国航空公司多以国外厂家给出固定的参考维修间隔对飞机进行预防性维修。该维修方式不仅会因“过修”带来大量的非例行维修工作，也可能由于“维修不足”，带来更大的成本和安全损失[2-3]。因此，根据航空公司飞机故障数据和工程经验制定最优维修间隔，对我国民航企业的发展具有重要意义。

针对维修间隔优化的问题，文献[4]利用半马尔可夫过程建模分析机械系统稳态可用度，忽略了修复时间对维护间隔的影响。文献[5]提出采用数值搜索方法求解飞机部件可用度预防性维修模型，没有考虑部件可靠度阈值的影响，且该方法较为繁琐且所得结果具有一定的误差。文献[6]利用两参数威布尔分布进行故障数据建模，确定出可用度最大情况下的预防维修间隔，其参数估计较三参数威布尔具有一定的误差。文献[7]在利用民机部件寿命分布确定最优维修间隔时，运用传统的三参数威布尔极大似然估计法对故障数据分布参数进行估计，该方法需要求解三个超越方程得到参数的估计值，由于有时位置参数似然估计值不存在，因此具有一定的局限性。

针对上述方法存在的问题，提出了一种基于可靠度和可用度的预防性维修间隔优化方法，以可靠度阈值为约束条件，将可用度作为目标函数，建立了预防性维修间隔优化模型。运用改进的三参数威布尔极大似然估计法对历史故障数据进行可靠性分析，并通过遗传算法进行模型优化求解，制定出合理的维修间隔，减少了非例行维修工作，降低了企业飞机维护成本。

2 预防性维修间隔方法确定

定时维修包括定时拆修和定时报废，其确定预防性维修间隔的方法相同，且仅适用于具有耗损期的产品[6]。因此，应当分析设备的失效寿命类型，从而判断其是否适于进行预防性维修工作。

优化预防性维修间隔的步骤一般包括：可靠性数据分析与预防性维修模型优化。维修间隔优化常用方法有三种[8]：（1）最小维修费用原则；（2）有效度最大原则；（3）达到一定的可靠性和安全性水平。综合考虑以上是三种方法，提出采用基于可靠性与可用性的维修间隔优化方法，在保证部件可靠度的同时，提高维修任务的可用性，从而提高经济效益。预防性维修间隔优化流程，如图1 所示。

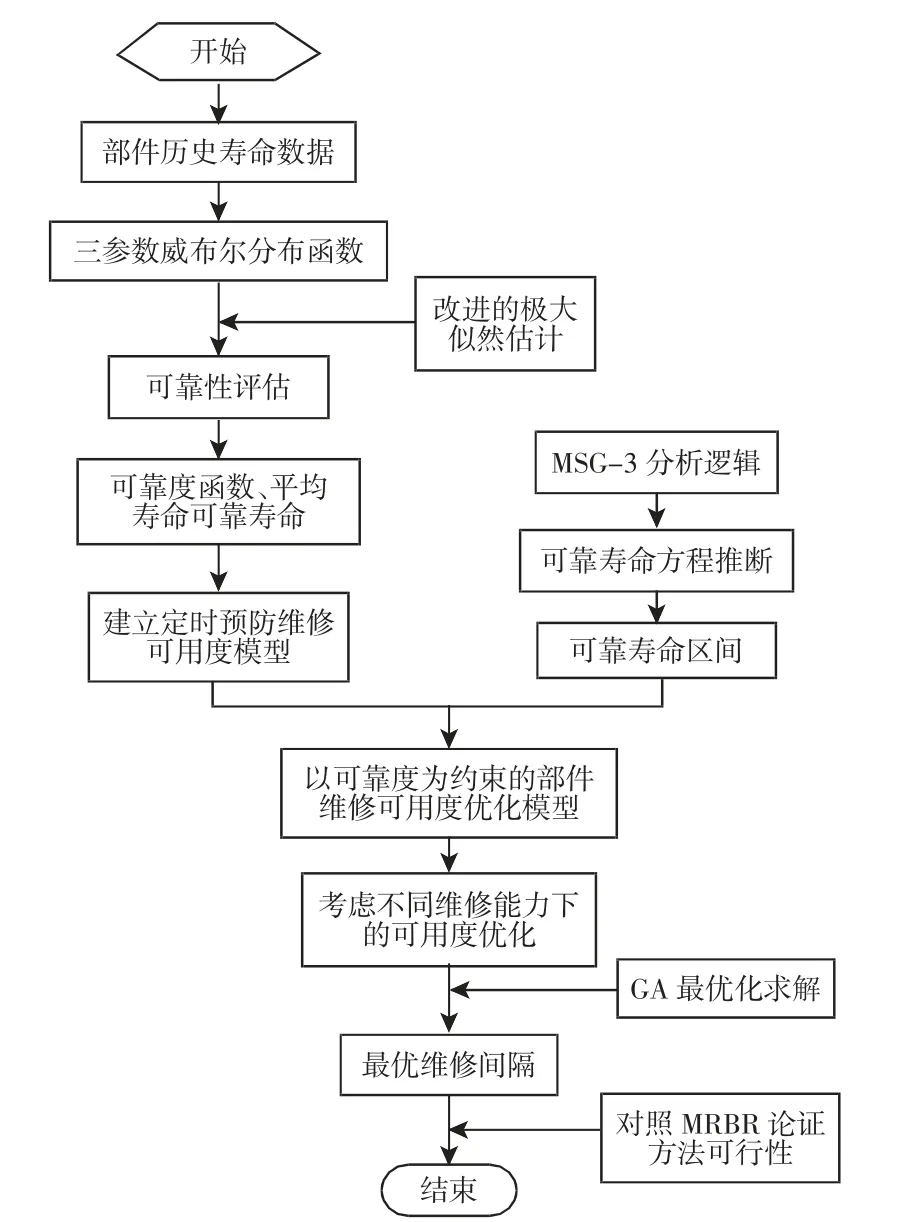
图1 民机预防性维修间隔优化流程Fig.1 Civil Aircraft Parts Maintenance Interval Optimization Process

3 民机部件可靠性评估

3.1 威布尔分布

威布尔分布包括二参数和三参数分布两种形式，对于二参数威布尔分布，在对现场数据进行可靠性评估时，其参数估计常带来较大的误差，而对于具有以耗损失效为特征的民机机械部件寿命评估中，采用三参数威布尔来分析部件的寿命分布，计算精度更高，更能反映民机机械部件可靠性的实际情况[8]。

三参数威布尔概率密度函数[9]为：

累计失效概率函数为：

式中：β>0—形状参数；η>0—尺度参数；γ≥0—位置参数。

当β＜1 时，为早期失效期，此时期不宜进行预防性维修；当β=1 时，为偶然故障期，在此期间进行预防性维护不影响故障率；当β＞1 时，为耗损失效期，在此时期内进行预防维修能提高部件的可靠度。

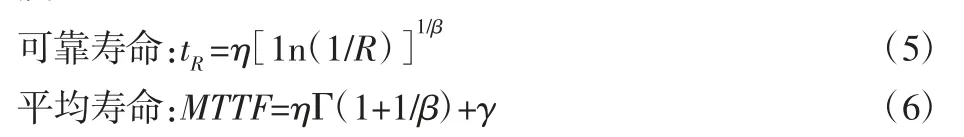
3.2 三参数威布尔参数估计

三参数威布尔参数估计方法较多，常用的有：线性回归估计法，图解法和极大似然估计法。极大似然估计方法是利用总体的概率密度分布及其样本信息求解未知参数的估计量，在参数估计问题中占有重要地位，综合考虑采用改进的极大似然法来解决模型参数估计问题。

假设飞机某附件故障寿命总体T 服从形状参数为β、尺度参数为 η 和位置参数为 γ 的三参数威布尔分布，即：T～W（β，η，γ）

其对数极大似然函数为：

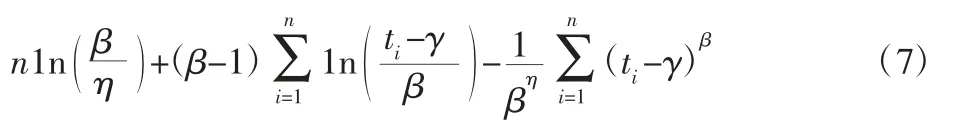
首先确定γ 估计值，然后极大似然估计另外两个参数。令∂lnL′/∂θi＝0，求解后得到 lnL′的极值。得到如下极大似然方程组：

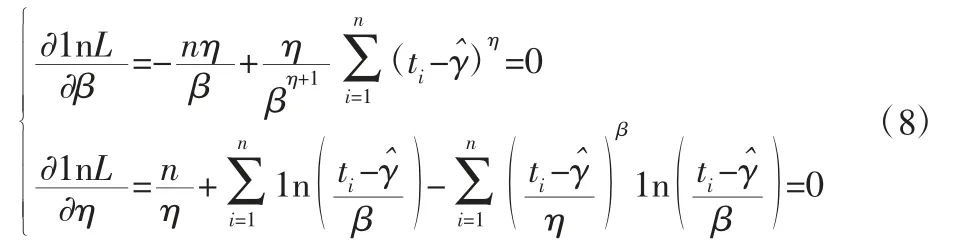
将故障寿命数据带入式（8）中，通过MATLAB 编程求出β，η，γ 的估计值由此可得到系统部件的故障寿命分布函数。

4 MSG-3 确定故障影响及可靠寿命

民机维修大纲的制定主要运用MSG-3 维修思想的原理，MSG-3 分析逻辑为上下两层，上层逻辑，如图2 所示。对重要维修项目明确功能故障和故障原因，根据逻辑图确定功能故障的故障影响类别，下层逻辑根据故障影响给出相应的维修方式。

在维修间隔的确定过程中，MSG-3 可以深入分析民机系统并选择合适的可靠度。由波音787PPH 提供的方法，得出不同故障影响类别下的可靠寿命方程[10]。对失效函数符合三参数威布尔分布的部件，结合式（4）建立了适合不同故障影响类型的维修项目可靠寿命方程：

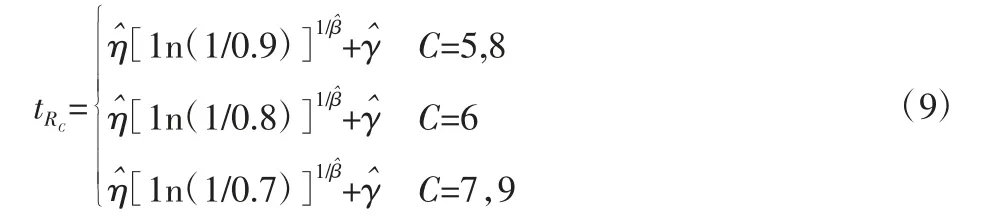
式中：C—故障影响类型，5、8 类可靠度取0.9；6 类可靠度取0.8；7 类可靠度取0.7。

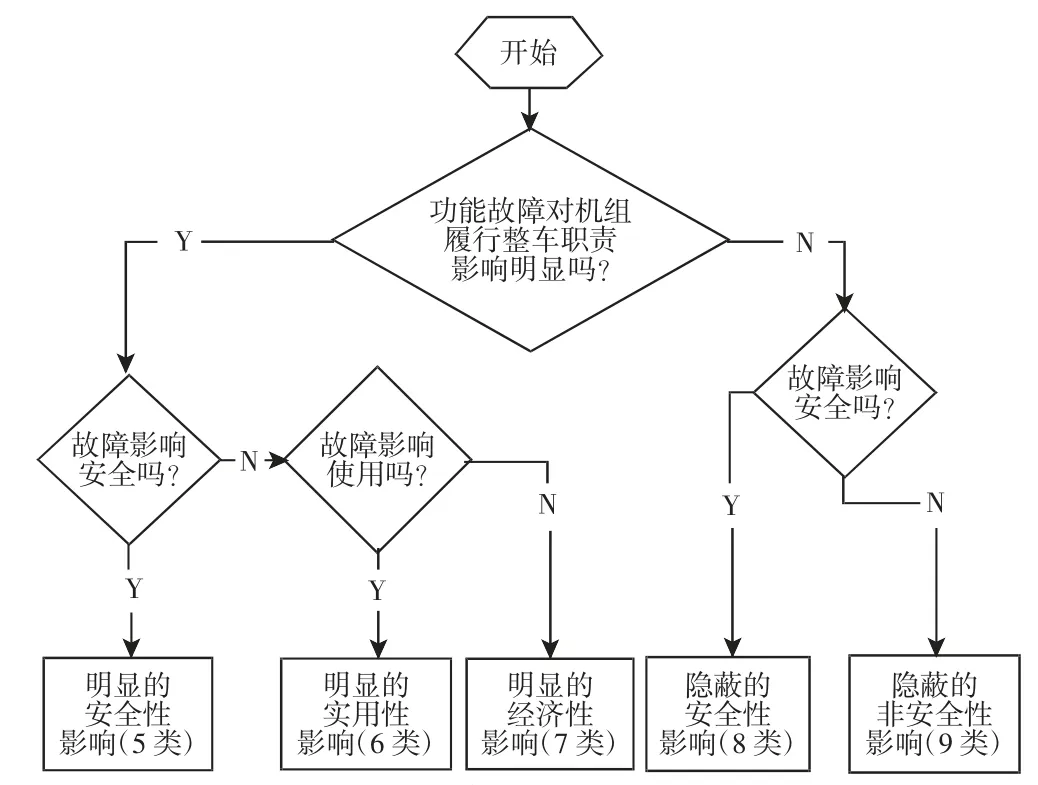
图2 MSG-3 故障后果影响类型判断流程Fig.2 MSG-3 Failure Consequences Impact Type Judgment Process

5 预防性维修间隔优化

5.1 维修间隔优化模型

可用度描述设备在某时刻投人使用的能力，是设备系统重要保障性能指标[11]。

式中：MUT—平均工作时间；MDT—平均不工作时间。

其中MDT 可表示为：

式中：Tp—预防性维修时间；Tf—修复性维修时间；T—预防性维修间隔。

可用度模型A（T）可表示为：

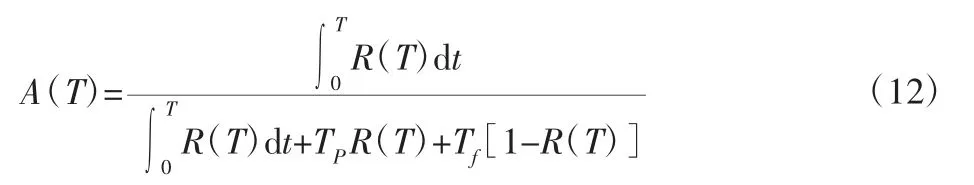
以可靠度阈值为约束条件，以可用度最大为目标，以预防性维修间隔为变量，建立优化模型如下：

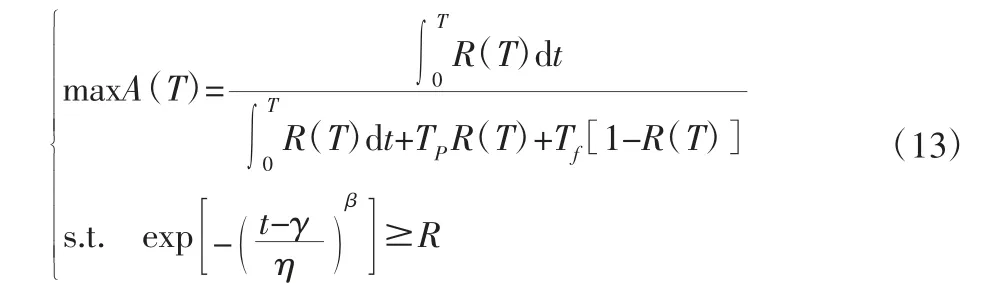
式中：R—部件在对应故障影响类型下的可靠度阈值。

5.2 模型求解

求解最优维修间隔时，一般通过可用度函数A（T）对T 求导，由于函数模型较为复杂，无法直接求A（T）对T 的导数，而遗传算法可跳出局部最优，并找到全局最优解[12]。因此，采用遗传算法求解方程得到最优维修间隔。在MATLAB 遗传算法工具箱（GA Toolbox）中，ga（）函数的基本调用格式为：

［T，fval，flag，out］=ga（ObjectiveFunction，nvars，opts）

其中，ObjectiveFunction 为描述目标函数的MATLAB 函数，nvars 为自变量个数，opts 可调用gaoptimset（）函数设置各种参数。函数调用结束后，返回的T 为最优预防性维修间隔，同时得出对应的可用度最大值即函数值fval。

6 实例分析

采集某航空公司空客A320 飞机高压引气活门（HPV）的数据（TSN），如表1 所示。故障信息时间段为2015 年1 月至2017年12 月，单位为FH。

表1 空客A320 高压引气活门（HPV）故障数据Tab.1 Airbus A320 HPV Fault Data

对于服从三参数威布尔分布的故障寿命数据，运用改进的极大似然估计方法进行MATLAB 程序计算，求解模型参数估计值，如表2 所示。

表2 三参数威布尔分布参数估计Tab.2 Three-parameter Weibull Distribution Parameter Estimation

由表2 可知，β>1 属于耗损寿命型，失效率随时间递增，可以通过优化预防性维修间隔，进行预防维修工作，提高部件的可靠性和使用寿命。

由此可得分布的可靠度函数为：

平均寿命 MTTF=ηΓ（1+1/β）+γ=20330

通过对HPV 故障后果的分析，符合MSG-3 中第5 类故障影响类别，即明显的安全性影响。对于安全类维护任务，将其可靠度限制在 0.9 以上，可靠寿命区为（4097，9629）。HPV 的可靠度曲线，如图3 所示。

图3 HPV 可靠度曲线Fig.3 HPV Reliability Curve

将各已知参数和寿命分布函数导入式（13）中，当可用度最大时，即不可用度最小，为了更直观地表述，讨论不可用度与预防性维修间隔关系。以可靠度阈值作为约束，将部件不可用度最小作为优化目标，讨论不可用度在区间（4097，9629）上的最小值情况。由于各维修单位的维修能力不同，现分别取Tp=1，Tf=10；Tp=0.5，Tf=10；Tp=1，Tf=20，利用 MATLAB 得出不可用度与预防性维修间隔关系，如图4 所示。

图4 不可用度与预防维修间隔关系图Fig.4 Unavailability and Preventive Maintenance Interval Diagram

由图4 可知，预防性维修间隔与预防性维修时间和修复性维修时间相关，在要求的可靠度范围内，即可靠寿命区（4097，9629）上，MATLAB 遗传算法工具箱求得可用度最大对应的维修间隔分别为 6573FH，6597FH，6633FH。当 Tf 相同时，Tp 越大维修间隔越小；当Tp 相同时，Tf 越大维修间隔越大；即最佳维修间隔的确定，与各维修单位的维修能力有关。查阅维修大纲（MRBR）可知，该维修任务间隔期为6000FH，可在一定程度上说明方法的可行性。利用本方法制定最优维修间隔，可在保证部件可靠度的同时，提高维修任务的可用性，从而提高经济效益。

7 结论

（1）对安全类的飞机部件，利用计算精度更高的三参数威布尔拟合故障数据分布，结合MSG-3 逻辑决断法，推断出可靠寿命区间。

（2）建立了以可靠度阈值为约束的可用度优化模型，采用遗传算法获得不可用度最小时的维修间隔，使制定的维修间隔在保证部件可靠性的同时提高利用率。

（3）通过分析优化结果可知，最佳维修间隔与各维修单位的维修能力有关，且与该维修任务的维修大纲参考值相比在合理的误差范围内，表明优化模型可行。