以微专题为突破口，有效攻破难题教学——以“函数不等式中参数范围问题教学”为例

广东省汕头市澄海华侨中学 (515800) 潘敬贞 山东省滨州市邹平县黄山中学 (256200) 韩景岗 广东省佛山市实验学校高中部 (528000) 袁锦前

函数不等式问题一直是高考考查的热点与难点问题，常以压轴题形式出现.已知不等式求参数范围问题是函数不等式问题中的典型问题之一，该类问题的求解对分析问题能力、转化与划归能力、代数变形能力、分类讨论能力、推理论证能力、运算求解能力等数学综合能力的要求比较高，主要考查数学抽象、逻辑推理、直观想象、数学运算等数学核心素养.因此，该类题一直是多年高考得分率比较低的题目，也是教学中的难点问题.

以微专题的形式，对函数不等式问题中的“已知不等式求参数范围问题”进行深入研究，并将其合理分类.对每一类问题都要做到明晰问题对象，理清求解思路，掌握解答程序等，可有效攻破这类难题的教学，提升学生解答这类问题的能力，提高他们的提高得分率，最终达到提高备考效益.本文主要针对近几年高考

考查函数与导数解答题中有关“已知不等式求参数范围问题”进行分类，并且对每一类问题结合实例给出一般求法.

1 求与函数最值有关的不等式解得参数范围

该类问题的求解，首先要讨论函数的单调性，从而得出函数的最值，最后直接解与函数最值有关的不等式即可求出参数的取值范围.该类问题主要考查分类讨论能力、代数变形能力、推理论证能力、运算求解能力等，主要考查数学抽象、逻辑推理、直观想象、数学运算等数学核心素养.

例1 (2017全国Ⅰ卷文21)已知函数f(x)=ex(ex-a)-a2x．(1)讨论f(x)的单调性；(2)若f(x)≥0，求a的取值范围．

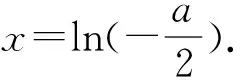
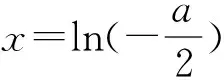
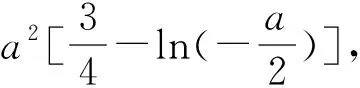
2 用函数“卡点”求得参数范围

该类问题的求解是通过讨论函数单调性并得出函数的最值之后，在解与函数最值有关的不等式时，由于所得超越不等式无法直接求出参数的取值范围，因此需要进一步构造新函数，研究新函数的单调性以及函数的“卡点”，最后得出参数的取值范围.该类问题较上一类问题，试题难度有进一步提高，解题长度进一步拉长，对解题能力提出了更高的要求.

例2 (2015全国Ⅱ卷文21)已知函数f(x)=lnx+a(1-x)．(1)讨论f(x)的单调性；(2)当f(x)有最大值，且最大值大于2a-2时，求a的取值范围．

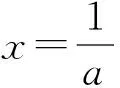
评注：本题的第(2)问先通过讨论函数单调性求得函数f(x)的最大值为-lna+a-1，进而根据题意得不等式lna+a-1<0，由于该不等式无法直接求出解，于是构造新函数即令g(a)=lna+a-1，并确定函数g(a)的单调性以及函数g(a)的“卡点”即g(1)=0，最后得出参数a的取值范围.

3 结合函数单调性与函数端点求得参数范围

该类问题综合性更强，问题的求解主要通过讨论函数单调性，结合函数的极值、端点值，综合分析判断函数符号，最后得出参数的取值范围.该类问题的求解不仅要有较强的分类讨论能力、代数变形能力、推理论证能力、运算求解能力，还要有敏锐的洞察力和较高的分析问题能力、转化与划归能力等.

例3(2010新课标卷文理21)设函数f(x)=x(ex-1)-ax2.(1)略；(2)若当x≥0时f(x)≥0，求a的取值范围．

解：(2)因为f(x)=x(ex-1-ax)．令g(x)=ex-1-ax，则g′(x)=ex-a．若a≤1，则当x∈(0,+∞)时，g′(x)>0，g(x)为增函数，而g(0)=0，从而当x≥0时g(x)≥0，即f(x)≥0．若a>1，则当x∈(0,lna)时，g′(x)<0，g(x)为减函数，而g(0)=0，从而当x∈(0,lna)时g(x)<0，即f(x)<0，不满足当x≥0时f(x)≥0．

综上所述，a的取值范围为(-∞,1]．

评注：本题的第(2)问，先通提公因式得f(x)=x(ex-1-ax)，又由于x≥0，所以令g(x)=ex-1-ax，此时将问题转化为研究：“当x≥0时g(x)≥0，求a的取值范围”的问题(这一步对降低解答难度、简化求解过程起到十分重要的作用)．通过对函数g(x)得出，当a≤1时函数g(x)在(1,+∞)上为增函数，又g(1)=0，所以当x≥0时g(x)≥0，即f(x)≥0．当a>1时得出函数g(x)在(0,lna)上为减函数，而g(0)=0，从而当x∈(0,lna)时g(x)<0，即f(x)<0，不满足当x≥0时f(x)≥0．最后即可得出参数a的取值范围．

例4(2016年全国II卷文21)已知函数f(x)=(x+1)lnx-a(x-1).(1)略；(2)若当x∈(1,+∞)时，f(x)>0，求a的取值范围.

评注：本题的第(2)问解答思路与例3的解答思路基本相同，关键是讨论函数单调性以及考虑函数端点值，结合不等式即可得出参数a的取值范围．

例5(2019全国Ⅰ文20)已知函数f(x)=2sinx-xcosx-x，f′(x)为f(x)的导数．(1)证明：f′(x)在区间(0,π)存在唯一零点；(2)若x∈[0,π]时，f(x)≥ax，求a的取值范围．

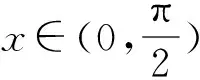
(2)由题设知f(π)≥aπ，f(π)=0可得a≤0.由(1)知，f′(x)在(0,π)上只有一个零点，设为x0，且当x∈(0,x0)时，f′(x)>0；当x∈(x0,π)时，f′(x)<0，所以f(x)在(0,x0)上单调递增，在(x0,π)上单调递减.又f(0)=0，f(π)=0，所以当时，f(x)≥0.又当a≤0，x∈[0,π]时，ax≤0，故f(x)≥ax.因此，a的取值范围是(-∞,0].

评注：本题的第(2)问，由题设知f(π)≥aπ，f(π)=0可得a≤0(这一步是降低本小题解答难度的关键)，再结合第(1)问得函数f(x)在区间(0,π)上存在唯一极大值，又f(0)=0，f(π)=0，因此可得出参数a的取值范围．

4 分离参数并新函数的最值得参数范围

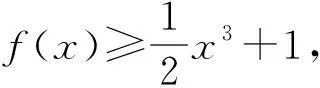
解：(2)①当x=0时，不等式为1≥1，显然成立，符合题意；②当x>0时，分离参数得a≥

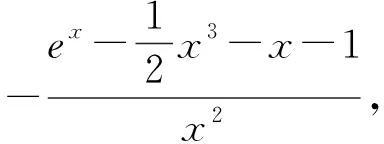
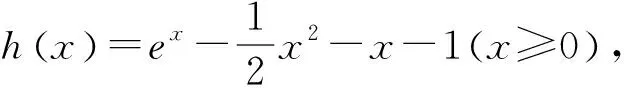
评注：本题的求解首先讨论x=0的情况，然后分离参数，构造新函数g(x)并求其最小值即可求出参数范围，思路清晰，考生也容易想到，但在求g(x)最小值的过程中遇到几点挑战：挑战之一是对g(x)求导后对函数g′(x)的分子进行因式分解；挑战之二是对函数g′(x)的分子中的因子符号进行判断并说明理由，在此过程中还用到了二次求导等，这两点问题对学生的运算求解能力、逻辑推理能力提出了极高的要求，也是众多学生的极大挑战，明知如何解而又不敢解或无法成功求解，这是无数学生心中的痛.

5 考题链接

1.已知函数f(x)=ax2+(a-2)x-lnx，(a∈R)．(1)讨论f(x)的单调性；(2)若f(x)≥0，求实数a的取值范围．(答案：(1,+∞))

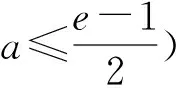
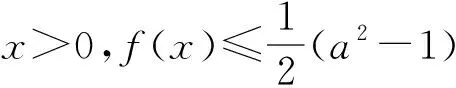
4.(2017全国卷Ⅱ文21)设函数f(x)=(1-x2)ex．(1)讨论f(x)的单调性；(2)当x≥0时，f(x)≤ax+1，求a的取值范围．(答案：[1,+∞))

5.(2015山东理21)设函数f(x)=ln(x+1)+a(x2-x)，其中a∈R．(1)讨论函数f(x)极值点的个数，并说明理由；(2)若∀x>0，f(x)≥0成立，求a的取值范围．(答案：[0,1])

6.(2015全国卷Ⅱ理21)设函数f(x)=emx+x2-mx．(1)证明：f(x)在(-∞,0)单调递减，在(0,+∞)单调递增；(2)若对于任意x1，x2∈[-1,1]，都有|f(x1)-f(x2)|≤e-1，求m的取值范围．(答案：[-1,1])

7.(2017全国卷Ⅲ理21)已知函数f(x)=x-1-alnx．(1)若f(x)≥0，求a的值；(答案：1)(2)略．

对于函数不等式问题，由于命题专家在命题时就已经将该类问题定位为压轴题，因此试题难度可想而知.但也不是考生不可解或教师不可教的试题.只要通过将考题合理分类，以微专题的形式，通过教师引导让学生明晰问题对象，理清求解思路，掌握解答程序，选编优秀的考题供学生训练后，加强对学生运算求解能力、逻辑推理等能力的培育，学生也能够攻克该类难题，从而提高学生的得分率.

压轴题、难题的教学对教师的专业水平提出了更高的要求，教师要有较高的解题能力，对考题要做到心中有数，熟悉命题规律，掌握命题技术，具有较高的命题能力，熟悉学生的成长规律和心理特征等.因此，只有多学习、多研究、多实践，尤其是解题实践、命题实践，多研究方可达到压轴题、难题教学的核心要求，方可真正达到高效备考的目标.