潮流作用下风电塔单桩基础冲刷数值模拟

唐冬玥 赵 鸣

（同济大学土木工程学院，上海200092）

0 引 言

风能已经成为当今最具规模化发展和商业化前景的可再生能源，海上风力发电受到了广泛的关注。单桩基础因其结构简单且承载力高，是近海风电塔的主要基础形式［1］。其主要通过上层土体传递侧向力，但近海潮流往复流动会在单桩基础周围，形成冲刷坑，影响其动力特性［2］。

基于经验方法和半经验半理论方法，学者们建立了单向流下的基础周围最大冲刷深度公式［3］。国内主要使用的是公路工程水文勘测设计规范中建议的65-1 修正式和65-2 式［4］，国外比较常用的有美国联邦公路署推荐的HEC-18 公式［5］和Sheppard-Melville方程（S-M方程）［6］等。

世界上首次提出潮流水流下桥墩局部冲刷的应用规范是2000 年的美国行业规范《潮汐河道冲刷》［7］。关于双向流下海洋结构物基础周围冲刷最大深度，学者们主要是通过与单向流计算结果对比［8-10］，或者是基于桥墩冲刷深度测量，如韩海骞的潮流作用下桥墩局部冲刷深度计算公式［11］。

目前的研究中对桩-土-潮流相互作用的冲刷机理认识不清［12］，因此本文对双向流下海上单桩基础风电塔冲刷进行研究。在研究方法选择上，虽然学者们可以通过实验方法获得可与规范对比的结果［13-14］，但是无法避免缩尺效应，相比之下数值模拟可以原型参数模拟［3］，现场观测可以得到工程实际数据。因此本文采用了数值模拟与现场观测相结合的方法进行研究，并通过参数分析推导双向流下大直径单桩基础风电塔基础周围的局部冲刷深度公式。

1 理论模型

1.1 水沙接触面模拟

当流动的水流受到桩基础阻挡，在桩周围形成湍流，带走了桩基础周围的土体。随着冲刷坑的发展，水沙接触面的高度、形状以及位置是不断变化的。为追踪多相混合体系中运动相之间界面，采用了自由表面追踪法（VOF）［15］。对于结构化网格，引入流体体积分数VF，即：对于一个网格单元，若VF在（0，1）范围内，则表示自由液面所在网格单元。

1.2 湍流模型

重整化群湍流模型（RNG）可以有效模拟旋转均匀剪切流，带分离的流动，适合模拟受桩阻挡后的水流绕流和涡旋，引入VF后的RNG湍流模型方程为

式中：xi为坐标轴方向，i=1，2，3为流体时均流速分量；Axi为xi方向上的可流动面积分数；ρ 为流体密度；k 为湍动能；ε 为湍动能耗散率；PT、GT为湍动能产生项；Dk、Dε为耗散项；C1、C2、C3为模型常数。

1.3 泥沙运动方程

冲刷过程中水流对泥沙的作用主要包括侵蚀、搬运和沉积三个部分。

1.3.1 泥沙起动

泥沙侵蚀即泥沙起动过程，采用时间和空间平均的临界希尔兹切应力理论计算泥沙的起动，计算公式为［16］

式中：ulift为泥沙起动速度；ρ 为流体密度；ρs为泥沙密度；d 为粒径参数；d*为无量纲参数；为考虑斜坡修正后的临界希尔兹数［17］；α 取值为夹带系数；θ 为局部希尔兹数，当局部希尔兹数超过临界希尔兹数，泥沙起动出现侵蚀。

1.3.2 泥沙搬运

泥沙搬运分为推移质搬运和悬移质搬运两种。

粒径较粗的泥沙沿床面作滚动、滑动或跃移被称为推移质。基于水流搬运泥沙所做的功与水流消耗的能量守恒的推移质输沙模型，推移质体积输沙率qb计算公式为

式中，Φ为无量纲的推移质输沙率。

计算公式为［18］

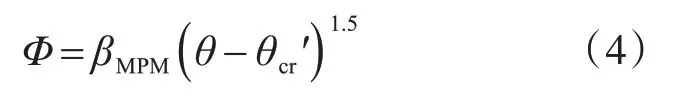
粒径较细的泥沙，由于紊动作用悬浮在水中并随水流一起运动被称为悬移质。悬移质泥沙浓度Cs可以根据泥沙扩散方程求解：

式中，D为扩散率。

从而根据浓度与流速乘积的垂线积分得到悬移质输沙率。

1.3.3 泥沙沉积

当推移质停止搬运或者悬移质沉降则发生淤积，泥沙沉降速度usetting计算公式为［17］

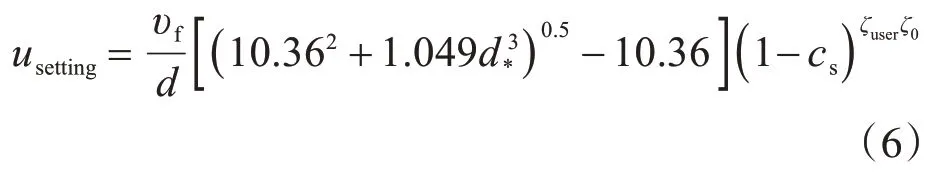
式中：υf为流体运动黏度；ζ0为用于考虑粒子间相互作用Richardon-Zaki相关系数。

2 双向流下单桩基础周围冲刷三维数值模拟

2.1 模型建立

基于上述冲刷理论方程，对江苏龙源蒋家沙风电场中风电塔建立模型。该风电场主要由桩径5.3 m 的4.0 MW 单桩基础风电塔组成，所在海域大部分水深在8 m 以内，为正规半日潮海区，潮流流速强劲，垂向平均流速最大达到2.36m∕s。地勘报告显示勘探深度范围内上部粉土、粉砂，下部为沉积物。得到模型计算参数如表1所示。

海床由沉积沙组成，其中夹带系数α 为0.018［16］，推移质系数β 取8［18］，初始泥沙厚度取8 m，流体高度为水深H，海床中掏空建立单桩，单桩为非变形实体类型。当受到单桩扰动的水流流速超过ulift，则泥沙侵蚀，沉积沙以推移质或悬移质搬运，当流速减小时，泥沙沉积。

对其建立结构化计算网格，以桩中心为原点，水流流动方向为X 方向，垂直流动方向为Y 方向，高度方向为Z 方向，三个方向计算范围分别为106 m、72 m、18 m。为提高计算速度，根据结构对称性采用半网格法。为提高计算精度，采用嵌套网格法对桩周围3D范围内网格加密，嵌套网格与外网格的尺寸比为1∶2。网格划分如图1所示。

表1 模型计算参数Table 1 Model calculation parameters

图1 网格划分Fig.1 Meshing block

水流初始速度为0，初始压强为Z向的静水压强。水流的边界条件如图2 所示，其中流速边界：设置X方向速度，其余方向速度为0；压力边界：各水流速度分量、紊动能和水压力的法向梯度均为零；对称边界：各通量均为零，仅有切向信息。需要注意的是，当流动方向改变时，入口与出口边界需要互换。

图2 边界条件Fig.2 Boundary conditions

周期用T 表示，每经过0.5T，流动方向改变。以2 小时40 分钟为一个周期，取计算周期为2T，则水流变向3次，桩侧参考点位分布如图3所示。

图3 桩周围参考点位置示意图Fig.3 Schematic diagram of the position of the reference points around the pile

2.2 仿真结果

取以桩为中心边长为60 m 的方形泥面区域，则风电塔单桩基础周围从0 至2T 时间段内的冲刷坑形状变化过程如图4所示。

在0.5T 和1.5T 时，最大冲刷深度位于桩左侧，在1T 和2T 时，最大冲刷深度位于桩右侧，双向流下最大冲刷深度的位置随着流速方向的改变而改变。最大冲刷深度为3.16 m。

从水流变向后一段时间内冲刷坑的形状变化看，可以发现，在双向流流体变向后的一段时间内，冲刷的主要作用是重塑冲刷坑的形状，转移最大冲刷深度的位置。

对图3 中桩侧各参考点位置处的冲刷深度绘制其随着时间的变化曲线，如图5所示。

根据图5可以看出，A至D的冲刷深度曲线与E 至H 点的冲刷深度曲线表现为两股交织的曲线，A 至D 点和E 至H 点随时间变化分别呈现相同的规律。0 至0.5T 和1T 至1.5T 时间范围内，流动沿X 轴正向，因此A 至D 点的冲刷深度大幅增大，而E 至H 点由于堆积的影响，冲刷深度有减小，在0.5T 至1T 和1.5T 至2T 时间范围内，流动沿X 轴负向流动，因此E 至H 点的冲刷深度大幅增大，而A至D点冲刷深度有所减小。

最大冲刷深度的位置随流动方向改变而改变，0 至0.5T 和1T 至1.5T 时间范围内，冲刷深度最大值位于C 点与D 点与桩圆心组成的扇形位于桩上游45°至70°范围内。0.5T 至1T 以及1.5T 至2T 时间范围内，冲刷深度最大值位于E 点与F 点与桩圆心组成的扇形位于桩上游45°至70°范围内。

图4 冲刷坑形状变化过程（单位：m）Fig.4 Change process of scouring pit shape（Unit：m）

2.3 与实测结果对比

2019 年3 月31 日对该风电场中某单桩基础风电塔测量其冲刷深度。首先记录水位高度h1=7.60 m；其次记录桩附近的水深h2=11.50 m，见图6，由此得到风电塔附近的冲刷坑深度为

根据上一节的数值模拟计算结果显示：在水深为8 m、水流平均流速1.89 m∕s 的双向流作用下，直径为5.3 m的单桩基础周围冲刷深度计算值为3.16 m；根据现场实测结果，5.3 m 桩径的周围冲刷深度的测量值为3.90 m。将在双向流下的数值模拟与现场实测的冲刷深度相比较，两者的误差在可以接受的范围内，因此本文对于近海风电塔在双向流下的单桩基础周围冲刷深度的数值模拟方法可行。

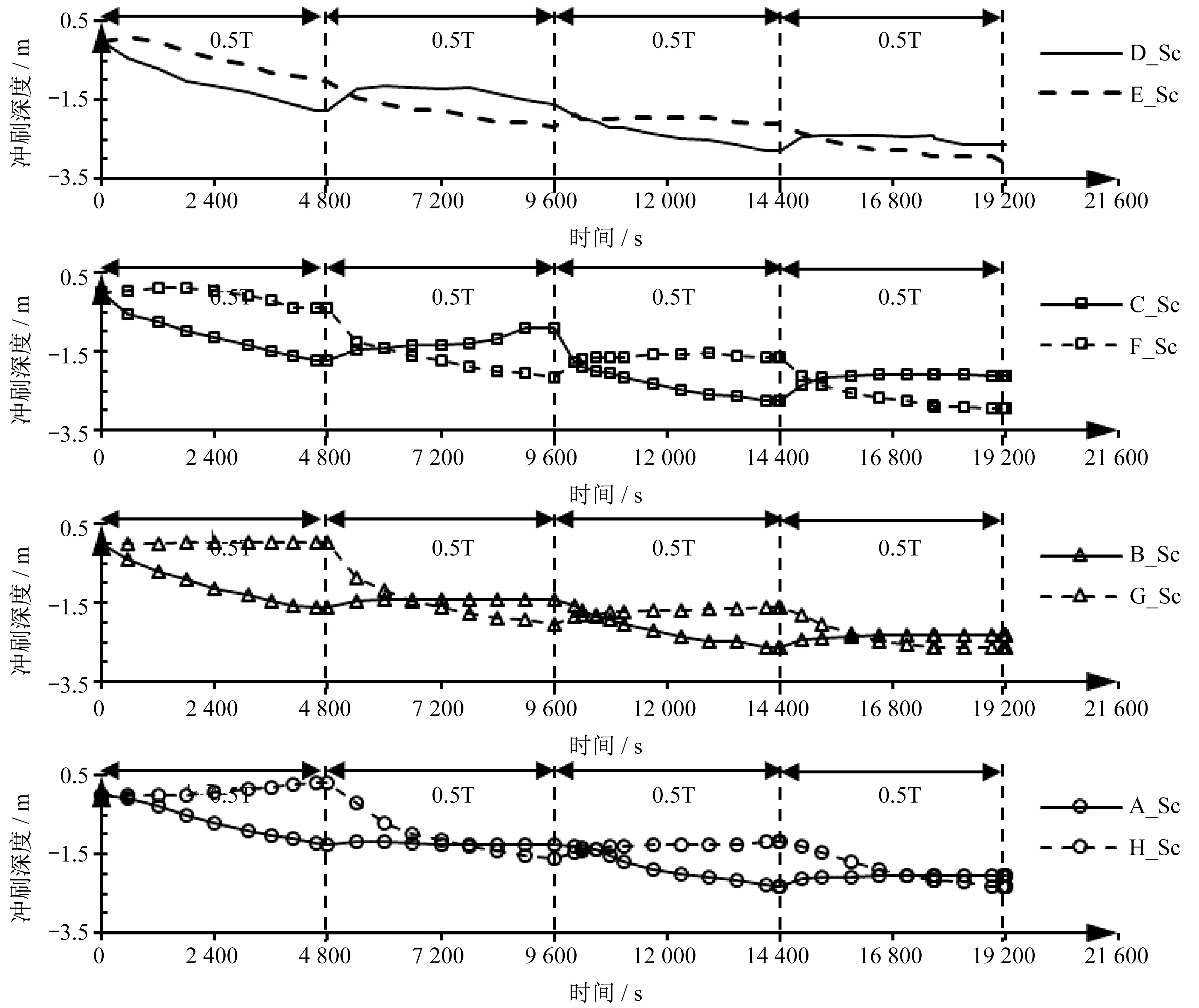
图5 桩周围参考点冲刷深度的时间变化曲线Fig.5 Time variation curve of scouring depth at the reference points around the pile

图6 测量单桩基础风电塔的基础冲刷深度Fig.6 Measuring the scouring depth around monopile foundation of one wind turbine

3 冲刷机理研究

以上一节工况作为工况1，分别改变变量流速、反向水深、桩径和土颗粒粒径数值，以及对于不改变流向的情况重新计算冲刷，其中区分正向和反向水深是考虑到退潮时水深小于涨潮水深，各工况的参数表见表2。

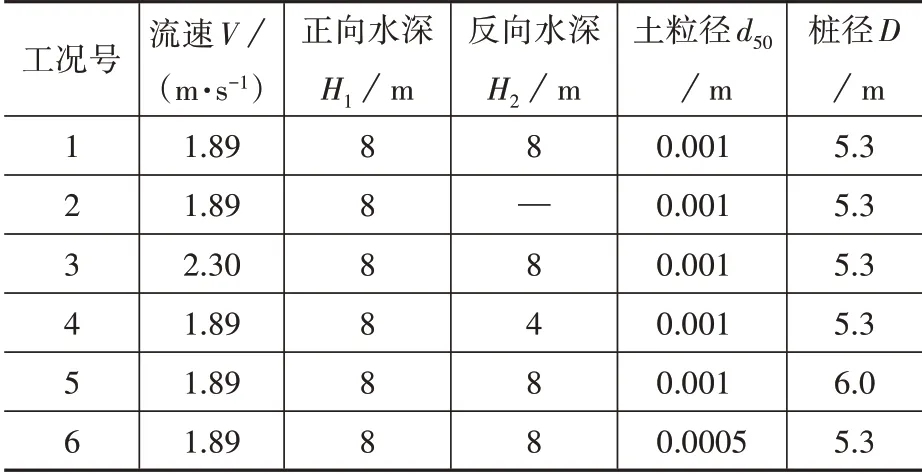
表2 各工况参数表Table 2 Parameters of multiple cases

各工况2T 对应时刻的冲刷坑计算结果见图7。

将各工况以及两个周期后的最大冲刷深度总结在表3 中，结合表2 可以得到，冲刷时长相同的情况下，流速增大，土颗粒粒径减小、桩径增大，最大冲刷深度增大，单向流的最大冲深大于双向流下，减小反向水深后最大冲刷深度减小。

图7 各工况冲刷坑形状（单位：m）Fig.7 Scour pit shape under different working conditions（Unit：m）

表3 各工况最大冲刷深度表Table 3 Maximum scouring depth for multiple cases

4 双向流下最大冲刷深度

将数值模拟得到的冲刷深度计算值与现行冲刷深度计算公式进行对比，包括了国内主要使用的65-1修正式和65-2式［4］，国外主要使用的Sheppard-Melville方程（S-M方程）［6］，计算潮流作用冲刷深度的韩海骞公式［11］，对比结果如表4所示。

表4 数值模拟与公式计算的最大冲刷深度比较Table 4 Comparison of maximum scouring depth calculated by numerical simulation and existing formula

从表4 可以看出，与数值模拟结果相比，各公式计算结果均偏大，其中65-1 修正式计算结果偏差最大，其次计算桥墩群桩基础在潮流作用下的冲刷深度的韩海骞公式，相较之下，65-2公式结果与计算结果最为接近，平均误差为17%，但是也可以发现该计算公式对各参数的改变不够敏感。因此需要重新推导双向流下风电塔桩基础的冲刷深度计算公式。双向流下冲刷深度S 主要取决于桩径D、来流流速V、正向水深H1、反向水深H2，泥沙粒径d50等，因此可以得出：

根据量纲和谐法则，可以得到：

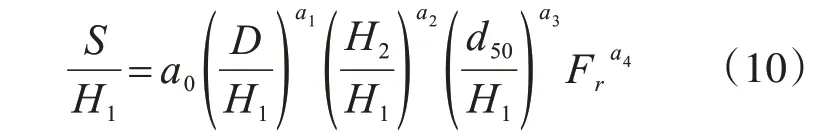
利用已有的数值模拟对式（10）参数进行率定，为了便于进行相关分析，对式（10）两边取对数，得

求解多元线性方程组，可以得到双向流下大直径单桩基础风电塔基础周围的局部冲刷深度公式：

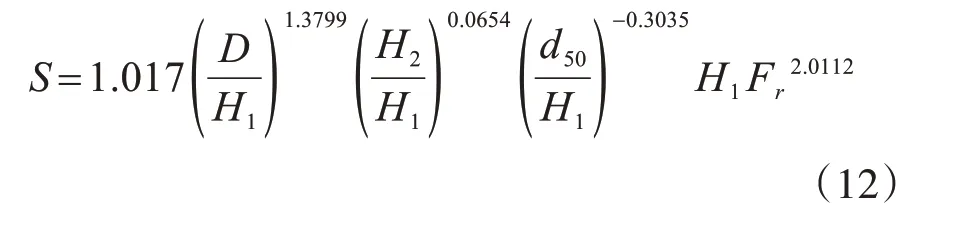
5 结 论

本文基于蒋家沙的风电塔，结合数值模拟和现场观测研究了双向流下单桩基础风电塔基础冲刷。计算了不同水利条件下的双向流下单桩基础风电塔冲刷，得到如下结论：

（1）本文通过数值模拟得到的冲刷深度与现场实测结果吻合良好，这验证了本文的双向流下单桩基础风电塔的冲刷深度的数值模拟方法。

（2）双向流下最大冲刷深度的位置随着流速方向的改变而改变，在流体变向后的一段时间内，冲刷的主要作用是重塑冲刷坑的形状，转移最大冲刷深度的位置。

（3）冲刷时长相同的情况下，流速增大，土颗粒粒径减小、桩径增大，最大冲刷深度增大。考虑双向流的往返水深的不对称性，若正向水深相同，减小反向水深后最大冲刷深度减小。

（4）基于数值模拟结果并根据量纲分析和多元线性方程求解得到了双向流下大直径单桩基础风电塔基础周围的局部冲刷深度公式。