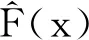一种改进的求解非线性方程组的Levenberg -Marquardt方法
伍珍香, 陈亮, 周童
(淮北师范大学 数学科学学院, 安徽 淮北 235000 )
0 引言
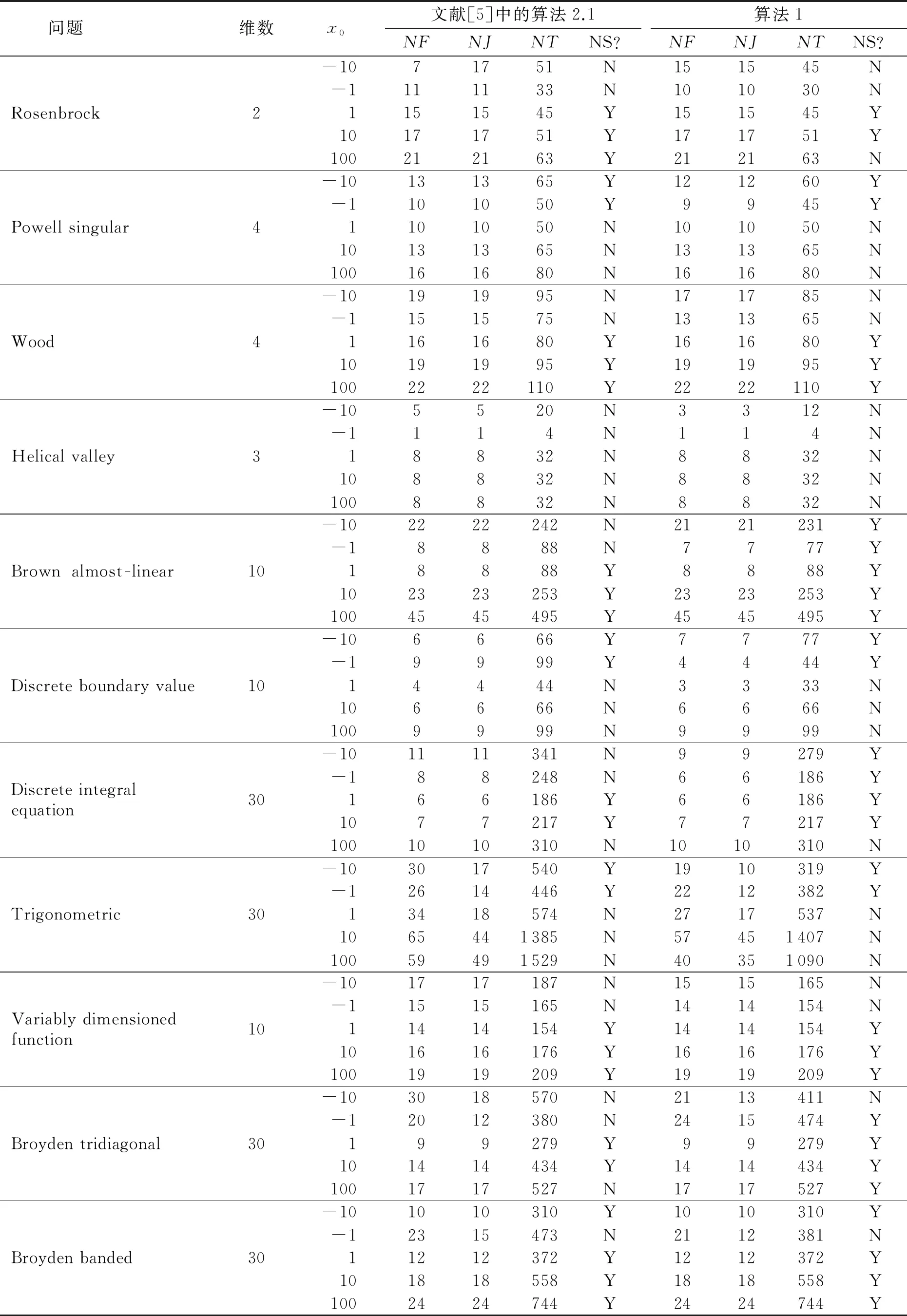
本文考虑如下非线性方程组
F(x)=0
(1)

(2)
其中Fk=F(xk),Jk(Jk=F′(xk))是F(x)在xk处的雅克比矩阵.当J(x)矩阵为Lipshitz连续且为非奇异时,牛顿法产生的迭代点列二阶收敛于方程组(1)的解;但当Jk是奇异矩阵或者接近于奇异时,牛顿步(2)无意义,即此时牛顿法不再适用.为此, Levenberg和Marquardt提出了解决上述问题的一个有效方法——Levenberg -Marquardt方法(简称LM方法)[1-2].LM方法的试探步为
(3)
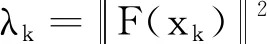
(4)

(5)
其中
(6)
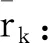
(7)
1 算法
新修正的LM法(算法1)的计算步骤如下:
步骤1 起始点x0∈Rn, 参数N0>0,μ0>m>0,ε>0, 0 (8) 步骤7 令k=k+1, 然后转到第1步. 算法1中要求μk≥m, 其中m是一个大于零的常数,即 μk≥m,∀k∈Ν. (9) 这一要求可由步骤1给定的初始条件和步骤6满足. 定义1N是Rn上的一个集合,使得N∩X*≠∅.如果存在一个常数c(c>0)使得 (10) (b)F(x)和J(x)在N(x*,b)上Lipshitz连续可微,即存在两个常数L1(L1>0)和L2(L2>0)使: (11) (12) 由假设(a)和(b)可知 (13) 引理2在假设1成立的情况下,对所有充分大的k, 有: (a)存在一个正的常数M>m, 使得 μk≤M. (14) (15) (16) J(x)=UΣVT= (17) 其中,U=[U1,U2,U3]和V=[V1,V2,V3]是两个正交矩阵,Σ1=diag(σ1,σ2,…,σr),σ1≥σ2≥…≥σr>0,Σ2=diag(σr +1,σr +2,…,σr +q),σr +1≥σr +2≥…≥σr +q>0.将Jk的SVD分解形式写成式(17)的形式,然后根据Jk的Lipshitz连续性以及矩阵摄动理论[10],得 因此有 (18) (19) 引理3[5]在假设1成立的条件下,对于充分大的k有: 证明(a)和(b)的证明可参考文献[5]中的引理3.3的证明,在此省略. 定理1在假设1成立的条件下,当δ∈(0,1)时,算法1产生的序列{xk}超线性收敛于方程组(1)的解;当δ∈[1,2]时,序列{xk}二阶收敛于方程组(1)的解. 证明根据式(10)、(11)、(15)和引理1有 由式(15)、(19)以及引理3有 因此 (20) 根据公式(10)、(11)、(12)、(19)和引理1有 (21) 为了验证算法1的有效性,本文利用试验对算法1和文献[5]中的算法2.1进行对比.测验函数F(x)是标准非奇异函数,来源于文献[11] .采用文献[12]中的方式对测验函数进行改进,结果为: 从表1中可以看出,在大部分测试问题中,算法1中的函数的计算次数、雅可比矩阵的计算次数以及总的计算次数大部分小于文献[5]中算法2.1的计算次数、雅可比矩阵的计算次数以及总的计算次数,由此说明算法1的计算量小于文献[5]中算法2.1的计算量,即算法1对非线性方程组的求解效率高于文献[5]中的算法2.1. 表1 数值试验数据和结果2 局部收敛性


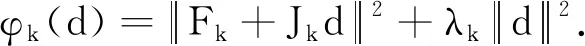



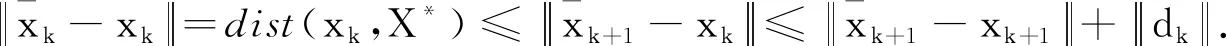
3 数值实验