一类具有阶段结构的时滞捕食系统的正周期解

吴罗义，郑航

(武夷学院 数学与计算机学院， 福建 武夷山 354300 )

0 引言

Lotka[1]和Volterra[2]提出捕食者的数学模型后，许多学者对其相关模型进行了改进，并对相关定性问题进行了研究[3-13].例如：魏凤英等[11]研究了食饵具有阶段结构和避难机能的捕食者系统的分支及其稳定性问题； Srinivasu等[12]研究了捕食者具有附加食饵的捕食者系统的相关性质，并讨论了附加食饵的“数量”对系统的影响.白玉珍等[13]研究了具有阶段结构和附加食饵与避难机能相结合的自治捕食系统的分支及其稳定性问题，其研究的模型为：

(1)

其中:x1(t)、x2(t)、y(t)表示未成年食饵、成年食饵和捕食者在t时刻的种群密度；m为避难参数，m∈[0,1]；k1(1-m)是捕食者的捕获率；h2表示捕食者处理单位数量的额外食物所需的时间；A′表示额外食物量.系统(1)中的其他数学符号的生物意义见文献[13].为减少参数以便计算，文献[13]还将系统(1)简化为了如下形式：

(2)

文献[13]考虑的是自治系统，且假设的系数均为正常数.而事实上，生态系统中很多因素是随时间不断变化的，如环境的周期性变化、繁殖的周期性变化等，因此研究非自治系统的周期解问题具有重要意义.本文考虑将系统(2)改进为非自治系统，并假设未成年食饵固有增长率a、 未成年食饵死亡率b、 成年食饵死亡率c、 捕食者死亡率r、 未成年食饵到成年食饵的成长率α和成年食饵内部竞争率d等参数为时间t的连续周期函数.由上述假设系统(2)可转化为如下非自治系统：

(3)

以下本文将应用迭合度理论探讨系统(3)至少存在一个正周期解的充分条件.

1 主要结果及其证明

(a)对任意的λ∈(0,1)， 方程Lx=λNx的解满足x∉∂Ω∩DomL；

(b)对任意的x∈∂Ω∩KerL,QNx≠0, deg{JQN,Ω∩KerL,0}≠0，

定理1系统(3)至少存在1个正周期解，若系统(3)满足以下3个条件：

(a) (1-m)(1+βρ)>ρ；

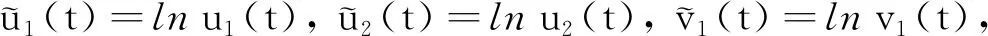
(4)

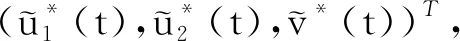
显然，在以上定义的范数下，X和Z为Banach空间.为了应用引理2， 本文定义以下映射：

由空间X、Z和映射L的定义可知:

以下在定理1的条件下求解满足引理2的有界开集Ω.由方程Lx=λNx，λ∈(0,1)得

(5)

再对式(5)的两边取绝对值，然后对其两边同时在[0,ω]上积分得

(6)

首先，根据定理1中的条件(a)、引理1以及系统(5)中的第3式可得

于是有

(7)

(8)

另外，由定理1条件中的(a)、引理1以及系统(5)中的第3式还可得

于是有

(9)

(10)

(11)

主要观察指标：针灸操作评分表，单人徒手心肺复苏术评分表，新疆医科大学外科基本技能评分表，体格检查考核评分标准（模块一、二、三、四）。考试通过率主要参照学生参与执业医师考试并获得资格证书进行计算。在本次研究中考察学生的就业率，即已就业人数除以毕业总人数乘以100%。

(12)

(13)

另外，由系统(5)中的第1式和第2式分别可得:

(14)

(15)

由式(14)和式(15)可得

(16)

综合式(8)、(10)、(11)、(12)、(13)和式(16)可得：

由定理1中的条件知代数方程组

(17)

下面证明Ω满足引理2中的条件(b).当(u1(t),u2(t),v(t))∈∂Ω∩KerL时， (u1(t),u2(t),v(t))是常向量，且‖(u1(t),u2(t),v(t))‖=H， 所以QNx≠0.因为ImQ=KerL=R3， 所以同构映射J可取恒等映射.由于式(17)存在唯一正解，因此直接计算即可得

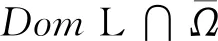
定理2系统(3)至少存在一个正周期解，若系统(3)满足以下3个条件：

(a) (1-m)(1+βρ)<ρ；

证明因证明方法与定理1相似，且只需注意函数的单调性即可，因此本文在此省略.

2 数值模拟

由(a)、(b)、(c)可知，所取的参数满足定理1的3个条件.在上述参数下系统(3)的解如图1所示.由图1可知，系统(3)的解是周期解.