基于蒙特卡洛模拟算法的欧冠淘汰赛抽签概率的研究

潘素娟，丁杰

(1.福建商学院 信息工程学院， 福建 福州 350012； 2.金融数学福建省高校重点实验室(莆田学院)，福建 莆田 351100； 3.厦门大学 经济学院， 福建 厦门 361005 )

0 引言

研究抽签概率不仅能促进统计和概率理论的发展，同时也能解决许多现实的问题，比如招标或投标项目、解决城市有限公共资源的供需矛盾、构建和运行马拉松赛事信息系统、设计和优化政府征收等.目前，国内外已有许多学者对抽签概率进行了研究，并取得了较好的研究结果[1-6].在体育竞技淘汰赛中，竞赛对象的不同可能会直接影响到竞赛的结果.为了解决竞赛过程中出现的机遇性强和竞赛结果的偶然性大等问题,通常采用抽签来决定竞赛对象，以此最大限度地保证竞赛过程的公正性和竞赛结果的合理性.目前，针对体育竞技淘汰赛的抽签方法主要有“1/4区公式控制抽签法”“1/2区逐级分区抽签法”“逐区双分抽签法”等方法.其中：“1/4区公式控制抽签法”能够较好地解决淘汰制抽签中“机遇”与“控制”的矛盾，但该方法的抽签过程较为繁琐，且进区概率存在失真性等问题[7].“1/2区逐级分区抽签法”虽然能够克服“1/4区公式控制抽签法”所存在的缺陷，但该方法并未考虑受随机因素影响的淘汰赛抽签[8].“逐区双分抽签法”虽然能够使得整个抽签过程做到最大限度的随机，但该方法并未考虑很多淘汰赛规则中所隐含的陷阱信息[9].目前为止，对淘汰赛中所隐含的陷阱还没有较好的模拟方法可以实现其对阵概率的求解.

蒙特卡洛模拟算法[10]是以概率统计理论为基础的一种计算方法，它可以随机模拟各种变量间的动态关系，把每一种不确定性对结果的影响以概率分布的形式表示出来，因此该方法可以解决数值解的求解问题.目前，已有学者利用蒙特卡洛模拟方法研究了彩票的概率模型，并取得了较好的效果[11]，但利用该方法来研究抽签概率的研究尚未见到报道.因此，基于上述难以求出对阵概率解析解的抽签概率问题，本文以2017—2018赛季的欧冠淘汰赛抽签概率为例，利用蒙特卡洛模拟方法求出进入欧冠淘汰赛的各支球队之间的对阵概率，并分别利用置信区间和分位点对模拟结果的可信度进行了分析.

1 研究设计

1.1 研究对象

欧冠2017—2018赛季的淘汰赛一共有16支球队.小组赛中以小组第1身份出线的球队有：曼联(A组，英超)、巴黎(B组，法甲)、罗马(C组，意甲)、巴萨(D组，西甲)、利物浦(E组，英超)、曼城(F组，英超)、贝西克塔斯(G组，土超)和热刺(H组，英超)；小组赛中以小组第2身份出线的球队有：巴塞尔(A组，瑞超)、拜仁(B组，德甲)、切尔西(C组，英超)、尤文(D组，意甲)、塞维利亚(E组，西甲)、矿工(F组，乌超)、波尔图(G组，葡超)和皇马(H组，西甲).

1.2 抽签规则

欧冠2017—2018赛季的淘汰赛采用抽签的办法确定竞赛对象.若对所有球队都不做任何约束条件，则每一支球队都可能抽到任何一个竞争对象，即抽签只是为了保证所有球队都有一个同等的机遇条件.但比赛组织方对欧冠2017—2018赛季淘汰赛的抽签制定了如下基本规则：

1)小组第1的球队对阵小组第2的球队.

2)同个小组的球队之间回避，如曼联不能和小组赛同组的巴塞尔对阵.

3)同国联赛的球队规避，如巴萨不能与同为西甲的皇马对决.

1.3 模型的建立

建立模型的目标是计算一个8×8的矩阵.矩阵内的元素对应的是两支球队之间的对阵概率，矩阵的行对应的是小组第1出线的球队(曼联标记为1，巴黎标记为2，罗马标记为3，巴萨标记为4，利物浦标记为5，曼城标记为6，贝西克塔斯标记为7，热刺标记为8)，矩阵的列对应的是小组第2出线的球队(巴塞尔标记为1，拜仁标记为2，切尔西标记为3，尤文标记为4，塞维利亚标记为5，矿工标记为6，波尔图标记为7，皇马标记为8).

1.4 抽签流程

抽签的流程为：第1轮，先从小组第1的球队中抽出1支球队，然后从它可能对应的(要考虑到规则2和规则3中的回避条款)小组第2中的对手中抽出1支球队，然后这两支球队组成对阵双方；第2轮，在剩下的球队中再次进行上一步操作.依据上述流程，只有完成第8轮抽签才可完成对阵抽签，但在实际抽签过程中会存在如下陷阱：

1)虽然理论上要进行8轮抽签才能确定最后的对阵，但在实际中抽到第7轮就已经能够确定最后的对阵情况.其原因是， 7轮抽签过后小组第1和小组第2的球队都只剩下1支，所以肯定是他们之间进行对决.

2)假设6轮过后，在剩下的球队中小组第1的球队是巴萨和贝西克塔斯，小组第2的球队是矿工和皇马.在这种情况下，经过6轮抽签即可确定对阵情况.因为小组第1的巴萨队不能对阵皇马队(同国联赛回避)，所以巴萨队只能对阵矿工队，由此可以推出贝西克塔斯队对阵皇马队.

3)在陷阱2)中，小组第2的皇马队不能对阵巴萨队(同国联赛回避)，所以皇马队只能对阵贝西克塔斯队，由此可以推出巴萨队对阵矿工队.

陷阱2)和3)在规则方面较为接近，但在有些情形中两者并不一致.例如：假设前2轮抽签结束后，对阵结果是巴黎队对阵皇马队，贝西克塔斯队对阵拜仁队.在这种情况下，由于存在同组规避和同国联赛规避的条款，因此小组第2的切尔西队对阵的球队只有巴黎、巴萨和贝西克塔斯，然而在巴黎队和贝西克塔斯队都已经被抽走的情况下，与切尔西队对阵的只能是巴萨队.上述情形所对应的就是陷阱3)，而非陷阱2).根据欧冠规则，同一个联赛原则上最多的欧冠名额是“3+1”个，其中3个球队直接进入欧冠小组赛，另1个球队参加附加赛(如果附加赛获胜就可以参加小组赛).另外，如果该联赛有1支其他的球队在上一年获得了欧联杯的冠军，那么该支球队也可以直接获得参加欧冠小组赛的资格.所以从理论上说，某个联赛参加欧冠小组赛的球队最多可以是5支.如果这5支球队都能小组出线，那么该联赛有5支球队能够参加欧冠淘汰赛.如果其中4支球队为小组第1，另1支球队为小组第2；或者其中4支球队为小组第2，另1支球队小组第1：那么和其他4支球队不在同一个组的那支球队不仅需要回避4支同国联赛的球队，还要回避同小组的球队.所以该球队需要回避的球队有5支，能够选择对阵的球队只有3支.这种最极端的例子出现在欧冠2017—2018赛季的淘汰赛抽签中，即切尔西队就是那支需要回避5支球队的球队.在这种最极端的情形下，经过两轮抽签后就可决定球队的对阵情况，即至少经过2轮抽签过后才可能会出现陷阱2)或陷阱3)的现象.

2 模拟过程

2.1 利用蒙特卡洛模拟计算对阵概率数值解的步骤

第1步 生成1个8×8且元素全部为0的矩阵.

第2步 根据规则先抽出一组对阵结果(即16支球队的8场对阵结果).如果2支球队之间的抽签结果为对阵，则在矩阵中对与该结果相对应的元素加1； 如果2支球队之间抽签的结果不为对阵，则矩阵中相应的元素不变.

第3步 重复步骤2，直到完成100 000次蒙特卡罗模拟.

第4步 将步骤3最终得到的矩阵中每个元素的最后累积值除以蒙特卡洛模拟的次数(100 000次)，即可得到对阵概率的数值解.

2.2 编程

2.1模拟步骤中的第2步的编程方法为：①根据规则任意抽取前两轮(因在最极端的情形下，前两轮也不会掉进陷阱2)或者陷阱3)).②从第3轮开始，首先观察每个小组第1的球队会不会出现只剩下1个可以选择的对手的情形.如果有，直接抽取出来；如果没有，就进入下一步.然后观察每个小组第2的球队会不会出现只剩下一个可以选择的对手的情形.如果有，直接抽取出来；如果没有，就可以和前两轮一样根据规则(即在同组回避和同国联赛规避的条件下)进行抽取.③第4轮到第7轮的抽签思路与第3轮相同.在所有的情形下，实际上不需要进行第8轮抽签，因为经过第7轮抽签后就可确定最终的对阵结果.经编程(见附录)得到的对阵概率如表1所示.

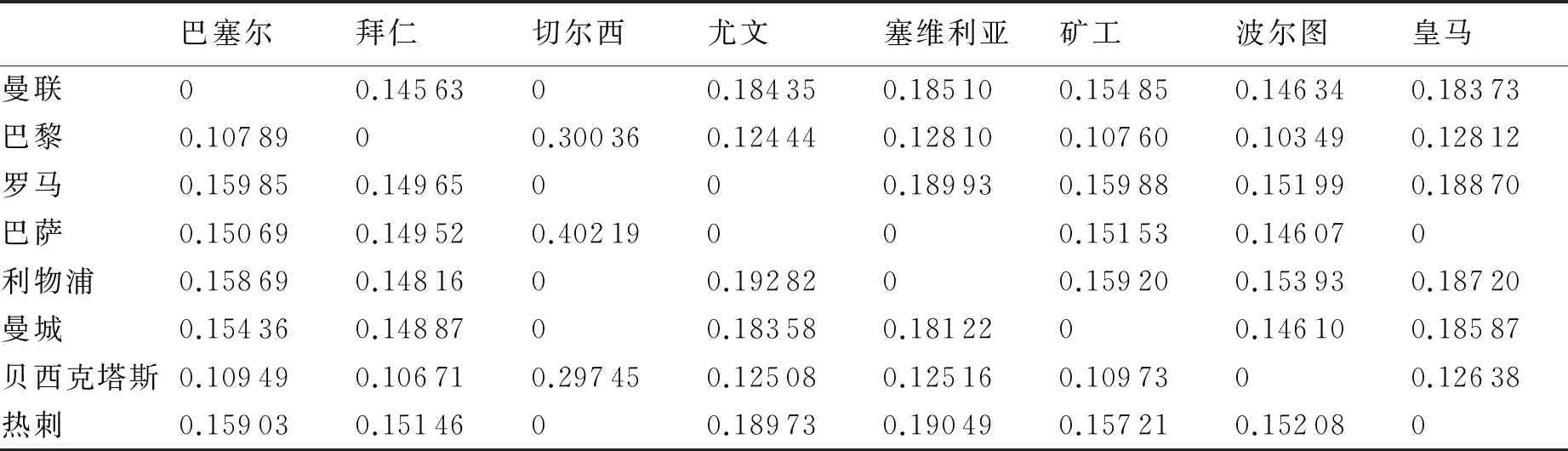
表1 各球队之间的对阵概率

3 可信度分析

利用蒙特卡罗模拟方法研究数值解问题时，若输入模式中的随机数并不是真正的随机数，则模拟及预测结果就会产生错误.为此，本文利用区间估计的方法(置信区间和分位点)对上述模拟得到的对阵概率结果进行可信度分析.

1)置信区间法.利用模型对对阵相关的64个参数进行100 000次蒙特卡洛模拟后发现，每次模拟都服从I.I.D.假设[12].为了验证可信度，对上述对阵概率的置信区间进行100次实验，每次实验均进行100 000次蒙特卡洛模拟.根据实验结果计算出的对阵概率的95%水平下的置信区间和99%水平下的置信区间的结果如表2和表3所示.由表2和表3可以看出，表中的置信区间都比较狭窄，说明本文提出的模型具有较高的可信度.

表2 对阵概率在95%水平下的置信区间

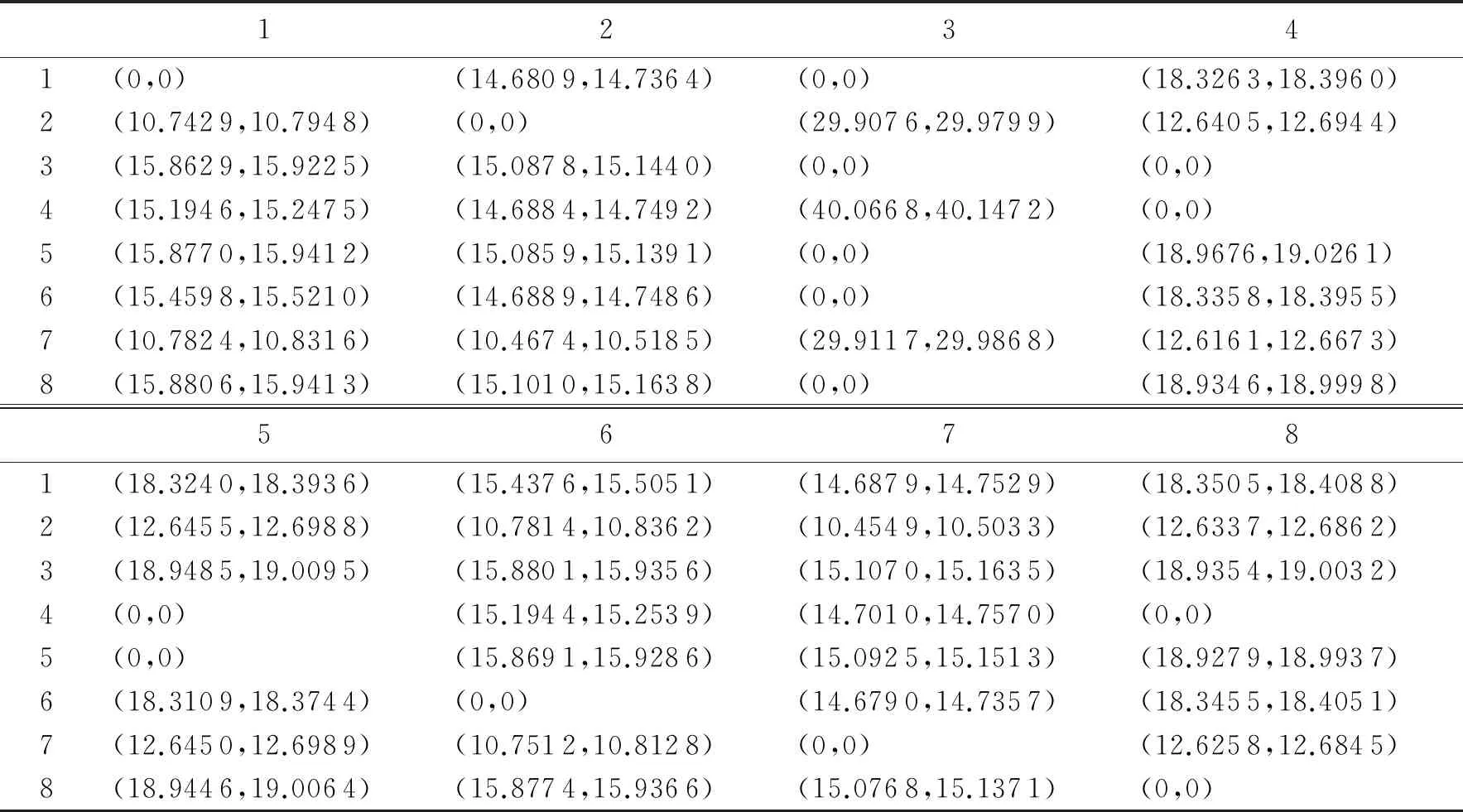
表3 对阵概率在99%水平下的置信区间

2)分位点法.以下通过分析两组分位点的结果来验证模拟结果的可信度.第1组为2.5百分位点到97.5百分位点，如表4所示；第2组为0.5百分位点到99.5百分位点，如表5所示.由表4和表5可以看出，表中的区间都比较狭窄，该结果再次说明本文提出的模拟方法具有较高的可信度.

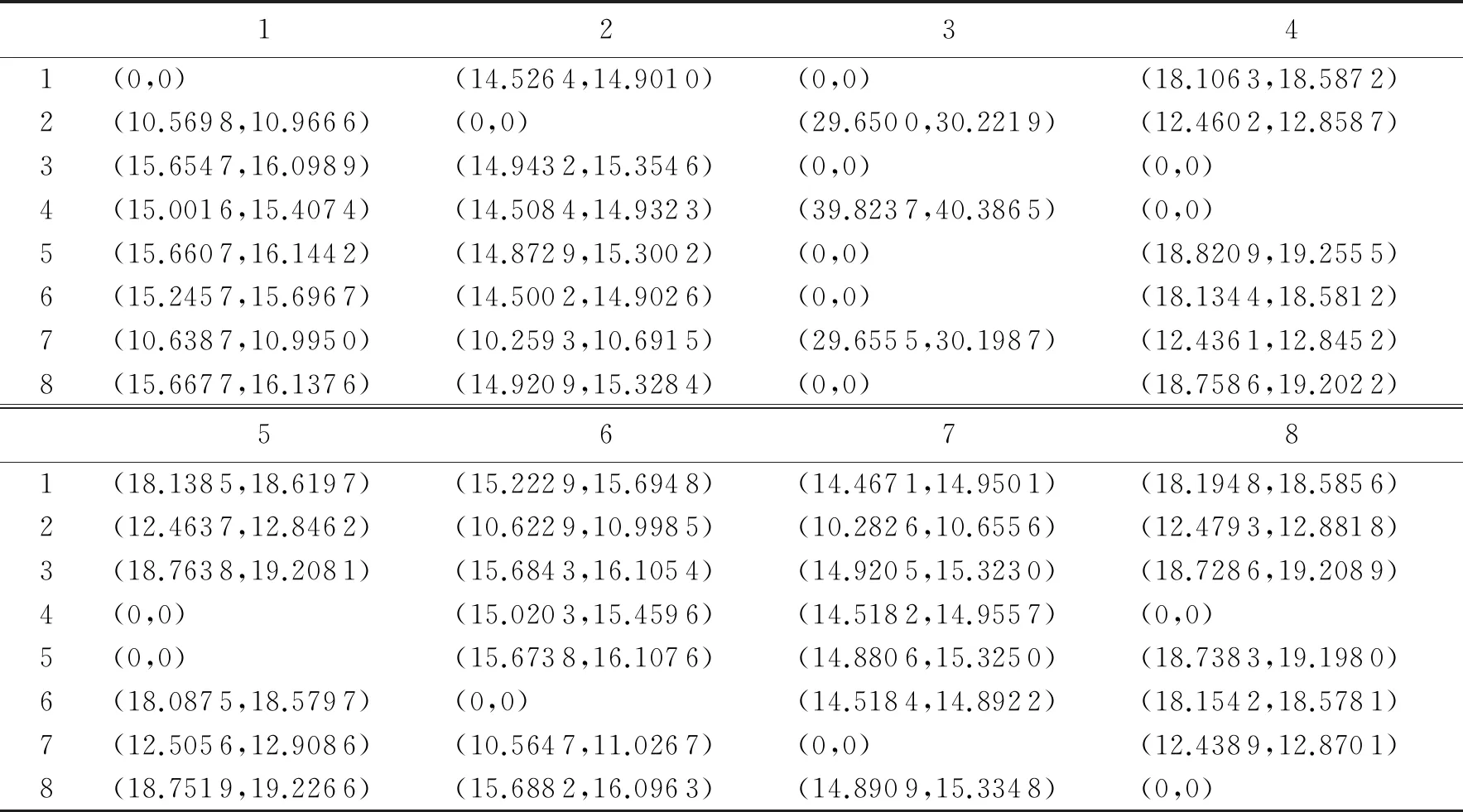
表4 对阵概率在2.5到97.5的百分位点

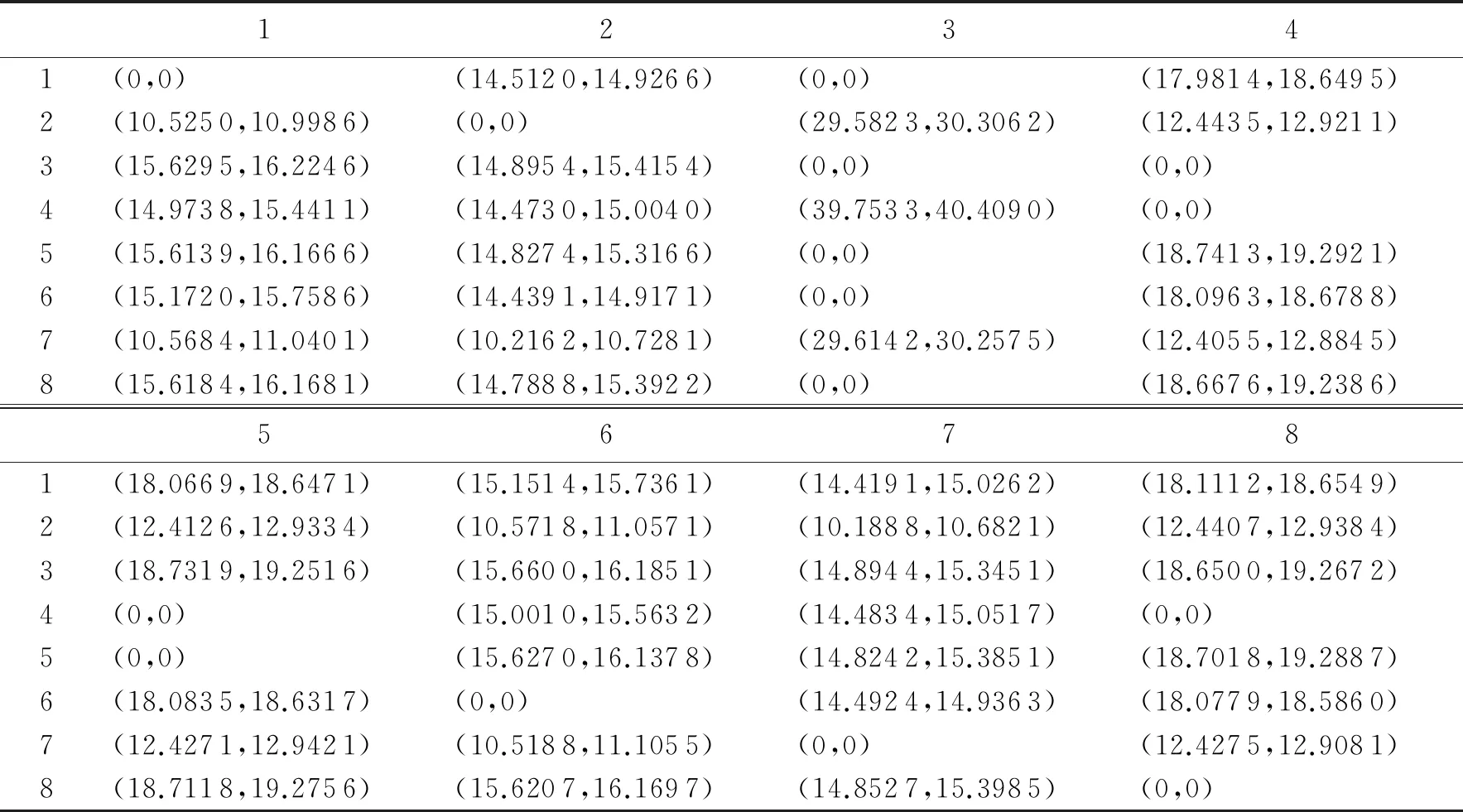
表5 对阵概率在0.5到99.5的百分位点

4 结论

本文通过对欧冠2017—2018赛季淘汰赛的抽签规则和抽签流程进行分析，利用蒙特卡洛模拟算法建立了一种新型的抽签概率模型，并给出了对阵概率的数值解.利用置信区间和分位点对模型计算所得的对阵概率进行可信度分析表明，本文的模拟方法具有较好的可信度.模拟结果显示，巴萨与切尔西对阵的概率约为40%(该结果与实际比赛结果相符)，由此再次表明本文模拟方法具有可靠性.另外，由于本研究已经考虑了最极端的情形，所以对于其他欧冠赛季，在不改比赛规则的情况下只要改变初始数据集就可以得到对阵概率.本文方法也可以为金融市场的风险管理、项目的招标与投标等问题的抽签提供借鉴.

附录：

R代码：

library(lubridate)

set.seed(1234)

sink(file="C:/Users/Ding/Desktop/UEFA Champions League.txt"，append=T)

n_1 <- 100000 # 100000 times Monte Carlos Simulations each experiment

n_2 <- 100 # 100 experiments

now()

result_all <- array(NA，dim=c(8，8，n_2))

for (x in 1:n_2) {

result_cum <- matrix(0，nrow=8，ncol=8)

FUN_1 <- function(a，b) {

result[a，1] <<- set_1[b]

result[a，2] <<- set_2_2[[set_1[b]]]

set_1 <<- setdiff(set_1，result[a，1])

for (j in 1∶8) {

set_1_1[[j]] <<- setdiff(set_1_1[[j]]，result[a，1])

}

set_2 <<- setdiff(set_2，result[a，2])

for (j in 1∶8) {

set_2_2[[j]] <<- setdiff(set_2_2[[j]]，result[a，2])

}

}

FUN_2 <- function(a，b) {

result[a，1] <<- set_1_1[[set_2[b]]]

result[a，2] <<- set_2[b]

set_1 <<- setdiff(set_1，result[a，1])

for (j in 1∶8) {

set_1_1[[j]] <<- setdiff(set_1_1[[j]]，result[a，1])

}

set_2 <<- setdiff(set_2，result[a，2])

for (j in 1∶8) {

set_2_2[[j]] <<- setdiff(set_2_2[[j]]，result[a，2])

}

}

for (k in 1∶n_1) {

result <- matrix(NA，nrow=8，ncol=2)

set_1 <- 1∶8

set_2 <- 1∶8

set_1_1 <- list(setdiff(1∶8，1)，setdiff(1∶8，2)，setdiff(1∶8，c(1，3，5，6，8))，setdiff(1∶8，c(3，4))，setdiff(1∶8，c(4，5))，setdiff(1∶8，6)，setdiff(1∶8，7)，setdiff(1∶8，c(4，8)))

set_2_2 <- list(setdiff(1∶8，c(1，3))，setdiff(1∶8，2)，setdiff(1∶8，c(3，4))，setdiff(1∶8，c(4，5，8))，setdiff(1∶8，c(3，5))，setdiff(1∶8，c(3，6))，setdiff(1∶8，7)，setdiff(1∶8，c(3，8)))

for (i in 1∶2) {

result[i，1] <- sample(set_1，1)

result[i，2] <- sample(set_2_2[[result[i，1]]]，1)

set_1 <- setdiff(set_1，result[i，1])

for (j in 1∶8) {

set_1_1[[j]] <- setdiff(set_1_1[[j]]，result[i，1])

}

set_2 <- setdiff(set_2，result[i，2])

for (j in 1∶8) {

set_2_2[[j]] <- setdiff(set_2_2[[j]]，result[i，2])

}

}

if (length(set_2_2[[set_1[1]]])==1) {

FUN_1(3，1)

} else if (length(set_2_2[[set_1[2]]])==1) {

FUN_1(3，2)

} else if (length(set_2_2[[set_1[3]]])==1) {

FUN_1(3，3)

} else if (length(set_2_2[[set_1[4]]])==1) {

FUN_1(3，4)

} else if (length(set_2_2[[set_1[5]]])==1) {

FUN_1(3，5)

} else if (length(set_2_2[[set_1[6]]])==1) {

FUN_1(3，6)

} else if (length(set_1_1[[set_2[1]]])==1) {

FUN_2(3，1)

} else if (length(set_1_1[[set_2[2]]])==1) {

FUN_2(3，2)

} else if (length(set_1_1[[set_2[3]]])==1) {

FUN_2(3，3)

} else if (length(set_1_1[[set_2[4]]])==1) {

FUN_2(3，4)

} else if (length(set_1_1[[set_2[5]]])==1) {

FUN_2(3，5)

} else if (length(set_1_1[[set_2[6]]])==1) {

FUN_2(3，6)

} else {

result[3，1] <- sample(set_1，1)

result[3，2] <- sample(set_2_2[[result[3，1]]]，1)

set_1 <- setdiff(set_1，result[3，1])

for (j in 1∶8) {

set_1_1[[j]] <- setdiff(set_1_1[[j]]，result[3，1])

}

set_2 <- setdiff(set_2，result[3，2])

for (j in 1∶8) {

set_2_2[[j]] <- setdiff(set_2_2[[j]]，result[3，2])

}

}

if (length(set_2_2[[set_1[1]]])==1) {

FUN_1(4，1)

} else if (length(set_2_2[[set_1[2]]])==1) {

FUN_1(4，2)

} else if (length(set_2_2[[set_1[3]]])==1) {

FUN_1(4，3)

} else if (length(set_2_2[[set_1[4]]])==1) {

FUN_1(4，4)

} else if (length(set_2_2[[set_1[5]]])==1) {

FUN_1(4，5)

} else if (length(set_1_1[[set_2[1]]])==1) {

FUN_2(4，1)

} else if (length(set_1_1[[set_2[2]]])==1) {

FUN_2(4，2)

} else if (length(set_1_1[[set_2[3]]])==1) {

FUN_2(4，3)

} else if (length(set_1_1[[set_2[4]]])==1) {

FUN_2(4，4)

} else if (length(set_1_1[[set_2[5]]])==1) {

FUN_2(4，5)

} else {

result[4，1] <- sample(set_1，1)

result[4，2] <- sample(set_2_2[[result[4，1]]]，1)

set_1 <- setdiff(set_1，result[4，1])

for (j in 1∶8) {

set_1_1[[j]] <- setdiff(set_1_1[[j]]，result[4，1])

}

set_2 <- setdiff(set_2，result[4，2])

for (j in 1∶8) {

set_2_2[[j]] <- setdiff(set_2_2[[j]]，result[4，2])

}

}

if (length(set_2_2[[set_1[1]]])==1) {

FUN_1(5，1)

} else if (length(set_2_2[[set_1[2]]])==1) {

FUN_1(5，2)

} else if (length(set_2_2[[set_1[3]]])==1) {

FUN_1(5，3)

} else if (length(set_2_2[[set_1[4]]])==1) {

FUN_1(5，4)

} else if (length(set_1_1[[set_2[1]]])==1) {

FUN_2(5，1)

} else if (length(set_1_1[[set_2[2]]])==1) {

FUN_2(5，2)

} else if (length(set_1_1[[set_2[3]]])==1) {

FUN_2(5，3)

} else if (length(set_1_1[[set_2[4]]])==1) {

FUN_2(5，4)

} else {

result[5，1] <- sample(set_1，1)

result[5，2] <- sample(set_2_2[[result[5，1]]]，1)

set_1 <- setdiff(set_1，result[5，1])

for (j in 1∶8) {

set_1_1[[j]] <- setdiff(set_1_1[[j]]，result[5，1])

}

set_2 <- setdiff(set_2，result[5，2])

for (j in 1∶8) {

set_2_2[[j]] <- setdiff(set_2_2[[j]]，result[5，2])

}

}

if (length(set_2_2[[set_1[1]]])==1) {

FUN_1(6，1)

} else if (length(set_2_2[[set_1[2]]])==1) {

FUN_1(6，2)

} else if (length(set_2_2[[set_1[3]]])==1) {

FUN_1(6，3)

} else if (length(set_1_1[[set_2[1]]])==1) {

FUN_2(6，1)

} else if (length(set_1_1[[set_2[2]]])==1) {

FUN_2(6，2)

} else if (length(set_1_1[[set_2[3]]])==1) {

FUN_2(6，3)

} else {

result[6，1] <- sample(set_1，1)

result[6，2] <- sample(set_2_2[[result[6，1]]]，1)

set_1 <- setdiff(set_1，result[6，1])

for (j in 1∶8) {

set_1_1[[j]] <- setdiff(set_1_1[[j]]，result[6，1])

}

set_2 <- setdiff(set_2，result[6，2])

for (j in 1∶8) {

set_2_2[[j]] <- setdiff(set_2_2[[j]]，result[6，2])

}

}

if (length(set_2_2[[set_1[1]]])==1) {

FUN_1(7，1)

} else if (length(set_2_2[[set_1[2]]])==1) {

FUN_1(7，2)

} else if (length(set_2_2[[set_1[3]]])==1) {

FUN_1(7，3)

} else if (length(set_1_1[[set_2[1]]])==1) {

FUN_2(7，1)

} else if (length(set_1_1[[set_2[2]]])==1) {

FUN_2(7，2)

} else if (length(set_1_1[[set_2[3]]])==1) {

FUN_2(7，3)

} else {

result[7，1] <- sample(set_1，1)

result[7，2] <- sample(set_2_2[[result[7，1]]]，1)

set_1 <- setdiff(set_1，result[7，1])

for (j in 1∶8) {

set_1_1[[j]] <- setdiff(set_1_1[[j]]，result[7，1])

}

set_2 <- setdiff(set_2，result[7，2])

for (j in 1∶8) {

set_2_2[[j]] <- setdiff(set_2_2[[j]]，result[7，2])

}

}

result[8，1] <- setdiff(1∶8，result[1∶7，1])

result[8，2] <- setdiff(1∶8，result[1∶7，2])

for (i in 1∶8) {

result_cum[result[i，1]，result[i，2]] <- result_cum[result[i，1]，result[i，2]]+1

}

#print(k)

}

#print(x)

print(now())

result_all[，，x] <- result_cum/n_1

}

result_mean <- matrix(NA，nrow=8，ncol=8)

for (i in 1∶8) {

for (j in 1∶8) {

result_mean[i，j] <- mean(result_all[i，j，])

}

}

result_sd <- matrix(NA，nrow=8，ncol=8)

for (i in 1∶8) {

for (j in 1∶8) {

result_sd[i，j] <- sd(result_all[i，j，])

}

}

result_all[，，1]

#### Confidence Interval

ci_95 <- data.frame(cbind(rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)))

#ci denotes confidence interval

colnames(ci_95) <- as.character(1∶8)

# 95% confidence interval

for (i in 1∶8) {

for (j in 1∶8) {

ci_95[i，j] <- paste0("("，round((result_mean+qnorm(.025)*result_sd/sqrt(n_2))[i，j]*100，4)，"，"，round((result_mean+qnorm(.975)*result_sd/sqrt(n_2))[i，j]*100，4)，")")

}

}

ci_95 # in percentage

ci_99 <- data.frame(cbind(rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)))

colnames(ci_99) <- as.character(1∶8)

# 99% confidence interval

for (i in 1∶8) {

for (j in 1∶8) {

ci_99[i，j] <- paste0("("，round((result_mean+qnorm(.005)*result_sd/sqrt(n_2))[i，j]*100，4)，"，"，round((result_mean+qnorm(.995)*result_sd/sqrt(n_2))[i，j]*100，4)，")")

}

}

ci_99 # in percentage

#### Quantile

# From .025th quantile to .975th quantile

quantile_1 <- data.frame(cbind(rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)))

colnames(quantile_1) <- as.character(1∶8)

for (i in 1∶8) {

for (j in 1∶8) {

quantile_1[i，j] <- paste0("("，round(quantile(result_all[i，j，]，.025)*100，4)，"，"，round(quantile(result_all[i，j，]，.975)*100，4)，")")

}

}

quantile_1 # in percentage

#### From .005th quantile to .995th quantile

quantile_2 <- data.frame(cbind(rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)，rep(NA，8)))

colnames(quantile_2) <- as.character(1∶8)

for (i in 1∶8) {

for (j in 1∶8) {

quantile_2[i，j] <- paste0("("，round(quantile(result_all[i，j，]，.005)*100，4)，"，"，round(quantile(result_all[i，j，]，.995)*100，4)，")")

}

}

quantile_2 # in percentage

sink()

rm(list=ls())

1/4+1/5.5+1/6+1/8.5+1/9+1/15+1/15+1/17+1/28+1/34

注：

1) set_1表示在第1小组中可抽的球队，set_2表示在第2小组中可抽的球队.

2) set_1_1表示一个长度为8的列表，其中的每一个元素都是一个向量.元素i表示第2小组中的第i支球队目前能够对阵第1小组的球队编号.

3) set_2_2表示一个长度为8的列表，其中的每一个元素都是一个向量.元素i表示第1小组中的第i支球队目前能够对阵第2小组的球队编号.

4)为了提高代码的效率，可以去掉显式循环，使用并行或者RCPP来提高R语言的循环速度.若需进一步提高模拟的精确度，可增加n_1和n_2的数值，由此则必然存在某个正数，只要n_1和n_2大于该数字就可满足设定的精确性要求.