绝热捷径技术在纠缠制备中的对比研究

邓灿，计新

(延边大学 理学院， 吉林 延吉 133002 )

0 引言

量子纠缠是量子计算和量子通信的基础，目前被广泛应用于密钥分配[1]、隐形传送[2]、密集编码[3]等领域.如何通过精确控制光子、原子等微观粒子制备出高保真度的纠缠一直是学者研究的主要内容.研究[4-5]显示,利用绝热演化可以精准地制备出高保真和对环境鲁棒的纠缠，但该方法因受到绝热近似的限制，使得量子系统的演化时间非常长，进而会导致退相干、损耗以及噪声积累等.2010年，陈玺等[6]首次提出了加速绝热演化过程的绝热捷径技术，并引起诸多学者的关注.近年来，学者们在陈玺等研究的基础上又提出了多种绝热捷径技术，主要有 Lewis -Riesenfeld (LR)不变量[7-8]、无跃迁量子驱动[9-10]、超绝热迭代[11-12]以及缀饰态[13-14]等.目前，绝热捷径技术已广泛应用于逻辑门构建[15]、纠缠制备[16]、原子冷却[17]、量子退火[18]、光机械[19]等领域，而且还由绝热捷径技术引申出了量子限速[20]、不确定性关系[21]、多重薛定谔绘景[11]以及最大冷却速率[22]等概念.但目前为止，对LR不变量、无跃迁量子驱动、超绝热迭代以及缀饰态这4种绝热捷径技术进行对比分析的文献尚无报道，为此本文在介绍这4种绝热捷径技术的基础上，从制备速度、保真度、激励脉冲、布居转移情况以及对环境的鲁棒性等方面对这4种绝热捷径技术制备纠缠态的方案进行对比分析，以为在实际应用中选择合适的纠缠制备方案提供参考.

1 4种绝热捷径技术的原理

1.1 LR不变量

LR不变量理论由Lewis和Riesenfeld[9]于1969年提出，该理论适用于由含时哈密顿量H(t)驱动演化的量子系统，系统的含时厄米不变量算符I(t)满足

(1)

(2)

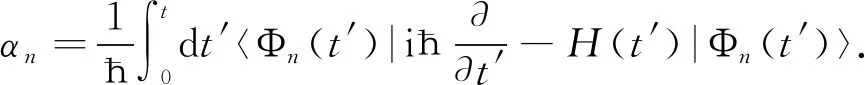
当系统的初态恰好是不变量的某个本征态时，系统会一直沿着初态演化而不会跃迁到其他的本征态，因此利用不变量的本征态可以构建出驱动系统演化的哈密顿量.构建该哈密顿时，可先对系统实施一个如下的幺正操作：

(3)

(4)

若I(0)与H(0)不对易，则I(0)的本征态|Φn(t)〉与H(0)的本征态不相同.同理，若I(tf)与H(tf)不对易，则I(tf)的本征态|Φn(tf)〉与H(tf)的本征态也不相同.因此，通过设置[H(0)，I(0)]=0和[H(tf)，I(tf)]=0， 即可实现系统哈密顿量的本征态和不变量的本征态在初始时刻和最终时刻相同，由此实现量子态布居的完美转移.

1.2 无跃迁量子驱动

无跃迁量子驱动方法由Berry[9]于2009年提出，该理论适用于研究含时量子系统，控制系统演化的原始哈密顿量H0为

(5)

H0的绝热近似解为|ψn(t)〉=ei ξn(t)|n(t)〉， 式中ξn为绝热相位，其表达式为

(6)

(7)

将式(7)代入HC D(t)得：

H(t)=H0(t)+HC D(t),

(8)

(9)

其中,HC D是非对角的厄米算符.当t<0和t>tf时，HC D(t)项变为0. 此时|n(t)〉可视为无跃迁哈密顿量H(t)的本征态，则无跃迁哈密顿量可以表示为

(10)

1.3 超绝热迭代

1987年， Berry[23]首次提出了超绝热迭代的概念.2012年， Ibanez等[11]在绝热迭代的基础上构建了绝热捷径通道，该技术使用的仍是一个由含时原始哈密顿量驱动演化的系统，其演化过程满足薛定谔方程

iħ ∂t|ψ0(t)〉=H0(t)|ψ0(t)〉.

(11)

(12)

然后结合式(11)和式(12)给出了如下相互作用绘景方程：

iħ ∂t|ψ1(t)〉=H1(t)|ψ1(t)〉.

(13)

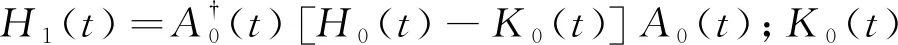
(14)

然后通过构建A0(0)=1， 使|ψ1(0)〉=|ψ0(0)〉成立，由此态函数可从|ψ0(t)〉=A0(t)|ψ1(t)〉演化为如下形式：

(15)

(16)

然后结合式(13)和式(16)给出了如下二次相互作用绘景方程：

iħ ∂t|ψ2(t)〉=H2(t)|ψ2(t)〉.

(17)

(18)

(19)

1.4 缀饰态

(20)

(21)

(22)

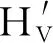
2 4种绝热捷径技术的对比

2.1 基于LR不变量的纠缠态制备

LR不变量技术最大的特点是在不改变原始哈密顿的形式下，可通过直接设计驱动脉冲的方式来加快制备纠缠态的速度，但在当前的实验条件下难以获得该驱动脉冲.本文基于控制变量的物理思想，对Wu等[24]和Huang等[25]在腔光纤耦合系统下基于LR不变量制备纠缠态的方案(特别是数值模拟结果部分)进行了对比分析，如表1所示.在表1中：tf为纠缠达到最高保真度时系统的演化时间； Ω(t)为驱动脉冲的拉比频率；λ、ε、υ、g为设置的相关参数；F(γ)和F(κ)分别表示保真度F与原子自发辐射率γ、腔光子泄漏率κ间的关系(在短光纤极限下，由于光纤光子泄漏对保真度的影响近似为零，因此只需考虑γ和κ对保真度的影响).

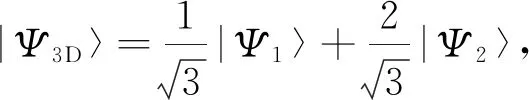
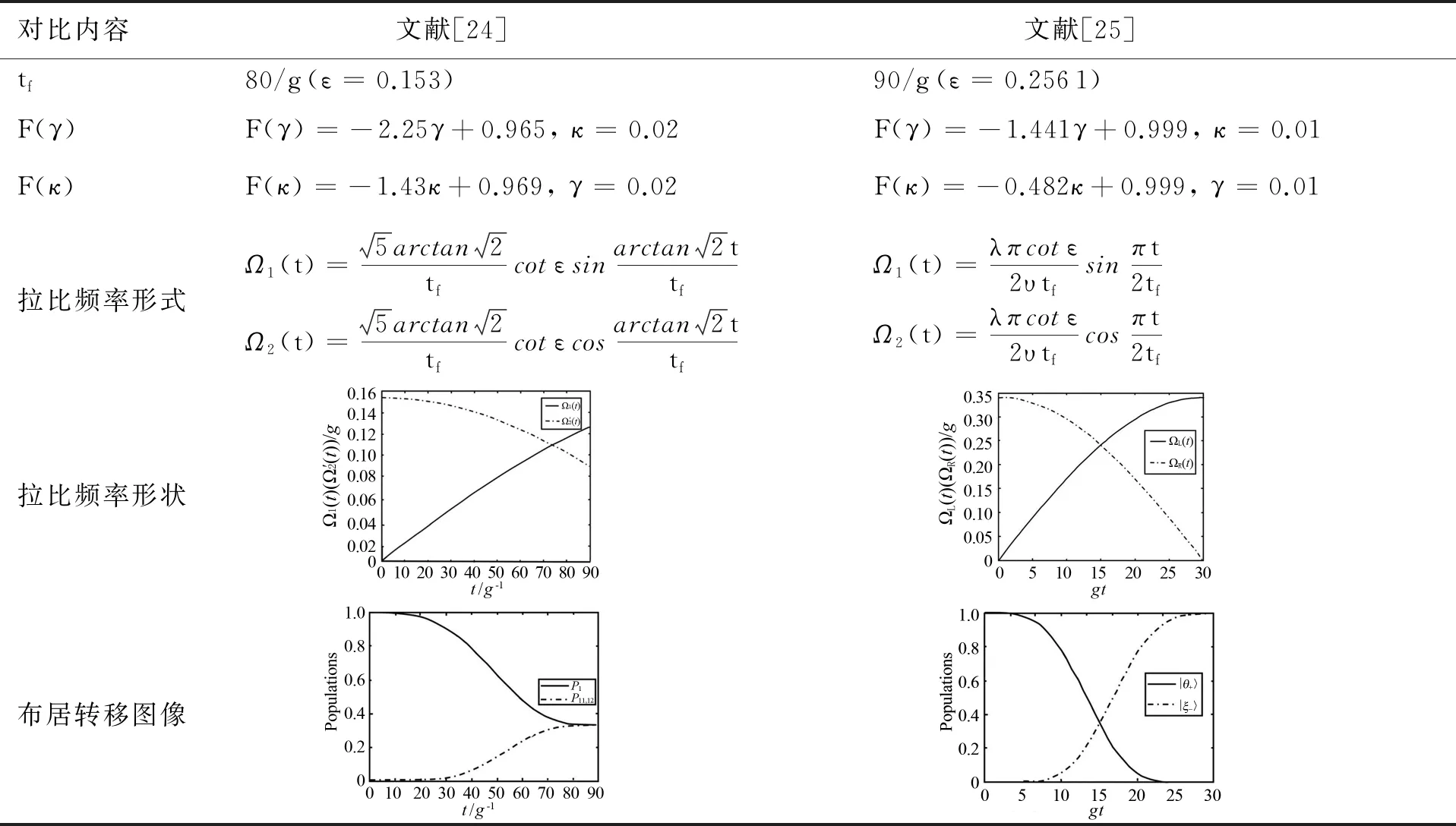
表1 基于LR不变量技术制备纠缠态的方案对比

2.2 基于无跃迁量子驱动的纠缠态制备

无跃迁量子驱动的关键是如何构造无跃迁哈密顿量HTQD， 虽然无跃迁量子驱动技术对激励脉冲没有严苛的要求，但因在当前的实验条件下无法直接构造出无跃迁哈密顿量，因此只能通过引入辅助能级、失谐量等方式才可构建出与无跃迁哈密顿量等效的任意物理可行哈密顿量HAPF.本文基于控制变量思想，对比分析了Huang等[27]和Chen等[28]在腔耦合模型下基于无跃迁量子驱动技术制备纠缠态的方案，如表2所示.在表2中：tf为纠缠达到最高保真度时系统的演化时间； Ω(t)为驱动脉冲的拉比频率； Ω0为驱动脉冲的振幅；t0、tc为设置的参数.F(γ)和F(κ)分别表示保真度F与原子自发辐射率γ、腔光子泄漏率κ的关系.

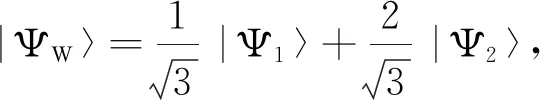
表2 基于无跃迁量子驱动技术制备纠缠态的方案对比

2.3 基于超绝热迭代的纠缠态制备

超绝热迭代技术首先是通过设计迭代相互作用绘景得到一系列的哈密顿函数，然后再从中选择适用于特定目的的哈密顿函数.利用该方案构建的超绝热哈密顿量与原始哈密顿量具有相同的形式，且制备出的目标态与原始哈密顿制备出的目标态也相同，但系统在演化过程中其激发态的布居很高，导致系统的耗散较大.本文基于控制变量的物理思想，对比分析了Huang等[29]和Wu等[30]在腔耦合模型下基于超绝热迭代技术制备纠缠态的方案，如表3所示.表3中：tf为纠缠达到最高保真度时系统的演化时间； Ω(t)为脉冲的拉比频率；τ、χ为相关的参数；F(γ)和F(κ)分别表示保真度F与原子自发辐射率γ、腔光子泄漏率κ的关系.

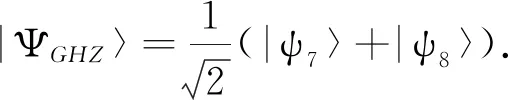
表3 基于超绝热迭代技术制备纠缠态的方案对比

2.4 基于缀饰态的纠缠态制备

缀饰态方案在不需要额外耦合的情况下即可实现对绝热过程的加速，同时通过选取合适的可控参数可以减少中间态的布居，从而减少系统的耗散和提高目标态的保真度.但在实际应用中，缀饰态方案所应用的系统可能会沿未知路径演化，由此会使得中间态的布居不受控制，进而增加系统耗散.基于控制变量的物理思想，本文对比分析了Kang等[31]和Zhang等[32]在超导量子干涉装置中基于缀饰态制备纠缠态的方案，如表4所示.在表4中：tf为操作时间； Ω(t)为脉冲的拉比频率；ζ、τ、χ为设置的参数；F(γ)和F(κ)分别表示保真度F与原子自发辐射率γ、腔光子泄漏率κ的关系.

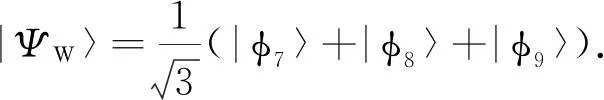
表4 基于缀饰态技术制备纠缠态的方案对比

3 结论

对基于LR不变量、无跃迁量子驱动、超绝热迭代以及缀饰态这4种绝热捷径技术制备纠缠态的方案进行对比分析发现，这4种绝热捷径技术均能加速系统演化过程，且均能有效地实现高保真度和对环境鲁棒的纠缠.另外， 4种绝热捷径技术在实现过程中也存在各自的局限性： LR不变量方案中的脉冲在当前实验条件下难以实现；无跃迁量子驱动方案制备的目标态与由原始哈密顿量驱动制备的目标态相比存在一定偏差；超绝热迭代和缀饰态方案虽具有更高的可行性(不需要耦合系统的初态、末态和引入额外的参数来构建哈密顿量)，但因系统演化路径包含激发态和演化路径不可控使得系统对原子自发辐射等耗散因素更加敏感，即其对环境的鲁棒性更弱.综上，在实际应用中应根据不同的实验条件和精度要求灵活运用上述4种绝热捷径技术来实现目标态的制备.