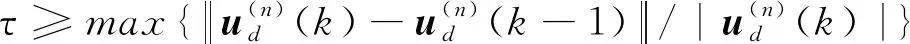Navier - Stokes系统降维模型中线性反馈控制的分析与逼近
赵锦玮,朴光日
(延边大学 理学院, 吉林 延吉 133002 )
0 引言
本文考虑如下Navier -Stokes系统的初边值问题:
(1)
其中: Ω是有界开集;ν=Re-1, Re为Reynolds数;u表示流体速度向量;p为压力;f为体积力.
Navier -Stokes方程能够反映黏性流体流动的基本力学规律,因此该方程常被用于解决工程技术中的流体力学问题.近年来,许多学者研究了Navier - Stokes方程最优控制问题的数学逼近理论,并且给出了求解非定常流动控制问题的数值方法[1-4].在对Navier - Stokes方程求解时,若采用有限元方法,则会出现一个非常大的非线性代数方程组,计算难度较大,尤其是对于反馈控制或最优化控制的问题.研究表明,利用降维法不仅可以保证计算的精度,节省计算机的内存,而且还可以大幅度提高计算效率.特征正交分解法[5]作为降维方法的一种,其实质是在最小二乘的意义下找到能够代表已知数据的正交基.在对Navier - Stokes方程降维模型的相关研究中,目前大多只是对其进行了数值分析,而对其进行理论分析的较少;因此,本文运用POD方法讨论Navier - Stokes系统降维模型的线性反馈控制问题,估计了线性反馈控制问题的降维模型解与有限元解之间的误差,并给出了计算降维模型解和跟踪速度问题的算法.
1 主要符号和Navier -Stokes方程的全离散格式

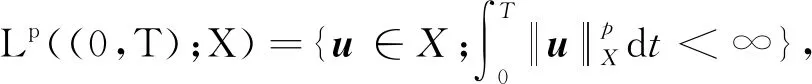
其中Di j(u)=(∂ui/∂xj+∂uj/∂xi)/2.
为了使给出的三线性形式具有反对称性[6],本文给出如下的三线性形式:
上述三线性形式具有如下性质[6]:
a3(w;u,v)=-a3(w;v,u),a3(w;u,u)=0,
(2)
(3)
F(x,t)=Ut(x,t)-νΔU(x,t)+U·U(x,t).
(4)

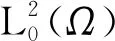
Xh={vh∈C0(Ω)∩X;vh|K∈P2(K),∀K∈h},
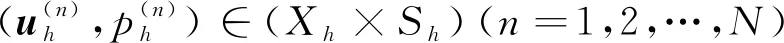
(5)
2 POD基的构造
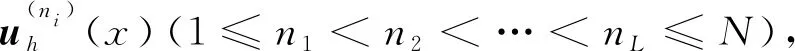
(6)
构造POD方法的目的是通过求标准正交基φj(j=1,2,…,L)使元素ui(1≤i≤L)与式(6)的d项和之间的均方误差最小,即通过求标准正交基φj(j=1,2,…,L)使
(7)
满足
(φi,φj)X=δi j, 1≤i≤d, 1≤j≤i,
(8)
令Xd=span{φ1,φ2,…,φd}, 且定义Ritz投影πh∶X→Xh(如果πh被限制为是从Xh到Xd的Ritz投影,则将其记为πd, 即πh|Xh=πd∶Xh→Xd和πh∶XXh→XhXd),
(9)

引理1[10]对于d(1≤d≤l)投影算子πd有如下不等式成立:
3 线性反馈控制问题的降维模型及其误差估计

(10)

(11)
(12)

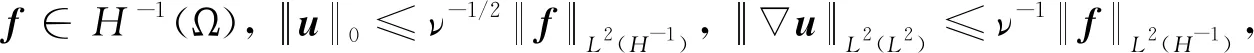

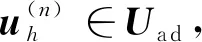

证明用式(5)减去式(11),并令vh=vd∈Xd⊂Xh可得
有
令vd=ψ(n), 则由式(9)和a3(w;u,u)=0可得
(ψ(n),ψ(n))+Δtνa1(ψ(n),ψ(n))=-(η(n),ψ(n))+(η(n -1),ψ(n))+(ψ(n -1),ψ(n))-
(13)

(14)
同理可得:
(15)
(16)
再由式(3)和Young不等式可得
(17)
同理可得
(18)
对于三线性形式,本文给出如下加强条件:
(19)
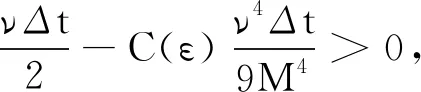
(20)

(21)
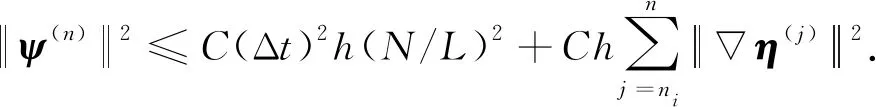

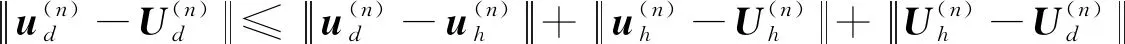
4 计算算法
(22)

(23)
则系统(22)可以转化成
(24)

为了求问题(22)的近似解,需将系统(22)线性化.系统(22)经线性化得
(25)
(26)
由文献[11]可知,将式(22)—(26)中的ud、wd、vd、pd、Xd、Sd分别用uh、wh、vh、ph、Xh、Sh代替,则其所得的离散格式与式(22)—(26)相同[11].