赏中华玩具 品数学文化

童广鹏 (河南省民权县高级中学 476800)

中华玩具历史悠久，在汉朝就已经出现了马骑、假面、偶人、泥车、瓦狗等诸多玩具． 在陶瓷玩具极大普及的唐朝，甚至流行丝绸制作的人形玩具． 数学作为一门严谨的科学，更是一种代代相传的文化． 因此对于体现了人文价值的中华玩具，我们的认识理应不断超越，追求圆满．

1 鲁班锁——榫卯穿插浑一体，天长地久匠心具

鲁班锁是较早流传于中华民间的智力玩具． 关于它的传说众多，相传是由春秋末期到战国初期的木匠鲁班为测试儿子聪明与否而发明，也有说是三国时期的诸葛亮根据八卦玄学所发明，因此它也叫“孔明锁”“八卦锁”． 它是一种三维组合结构，从外观看是严丝合缝的几何体，利用的是榫和卯的原理． 它不用钉子、绳子等工具固定，完全靠自身榫卯结构的连接支撑，看似简单，但其结构之间的巧妙契合却体现出了科学的本质，给现代数学以极大的启示．

例1鲁班锁(也称孔明锁、难人木、六子联方)起源于古代中国建筑的榫卯结构． 这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合，十分巧妙． 鲁班锁类玩具比较多，形状和内部的构造各不相同，一般都是易拆难装． 如图1，这是一种常见的鲁班锁玩具，图2是该鲁班锁玩具的直观图，每条棱的长均为2，则该鲁班锁的表面积为( )．

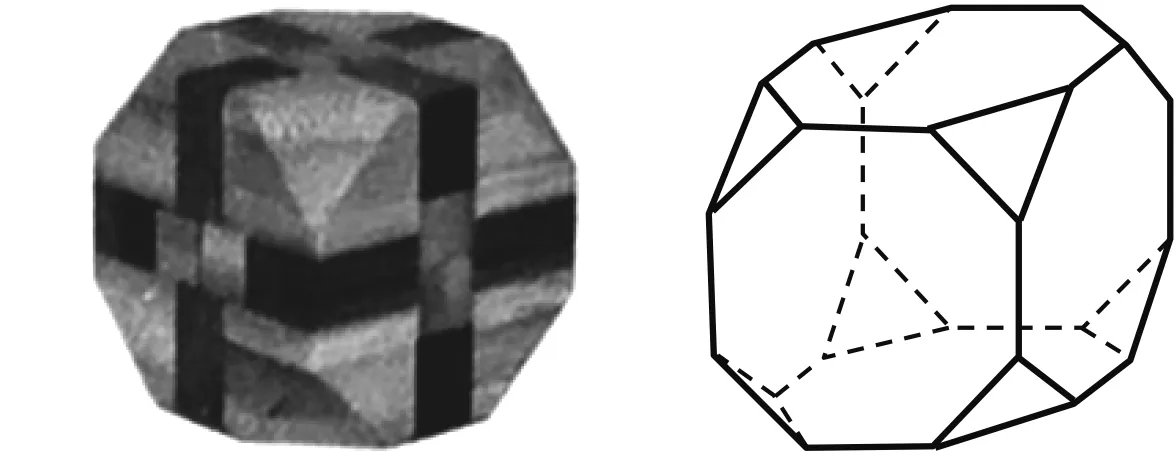
图1 图2

点评鲁班锁不仅是一种益智类玩具，也是一款极具东方韵味的装饰品． 其造型上的简洁、均衡与对称性，结构上的数理性和严谨性，功能上的娱乐性和教育性，人机上的合理性和舒适性，拼装过程中的次序性，用材上的质朴性，使其历经千百年来经久不衰． 本题将鲁班锁以文化题形式呈现，但万变不离其宗，在解题的过程当中不能偏离所学的数学公式．

2 陀螺——高速自转圆锥体，前进绵绵无绝期

陀螺是一种古老的传统民俗游戏玩具，为木制的圆锥形，上大下尖，用鞭子连续抽击一圆锥形陀螺，使之在平滑地面上旋转． 它历史悠久，山西夏县西阴村仰韶文化遗址(距今约五六千年)中曾出土陶制小陀螺． 陀螺是中国传统民俗体育游戏，流传甚广．

例2陀螺是汉族民间最早的娱乐工具之一，也称作陀罗，闽南语称为“干乐”，北方称为“冰尜”或“打老牛”，以前多用木头制成，现在多为塑料或金属制． 玩时可用绳子缠绕，用力抽绳，使它起立旋转． 现有一陀螺，其三视图如图3所示，其中俯视图中的△ABC为正三角形，则该陀螺的体积为( )．

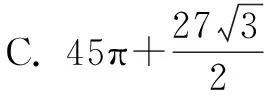
图3

点评本题以陀螺为载体，以跨学科、跨文化的多元视角引导学生感受数学的应用价值和潜在魅力，激发学生的学习情感，让学生学习到活生生的数学．

3 围棋——智力格斗八角笼，厚积薄发又一村

围棋是一种策略性棋类游戏，起源于中国，相传尧舜以棋教子，在春秋、战国时期，围棋已广为流行． 古时有“弈”“碁”“手谈”等多种称谓，属琴棋书画四艺之一，也被认为是当前世界上最复杂的棋盘游戏之一． 围棋使用格状棋盘及黑白二色棋子进行对弈，双方在网格交叉点上交替放置黑白两色棋子，落子后不能移动，围地吃子，以所围“地”的大小决定胜负．

图4

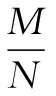
A． 1033B． 1053C． 1073D． 1093

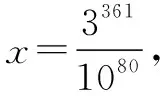
4 七巧板——七巧板里学问多，天下万物皆包罗

七巧板又称七巧图、智慧板，是一种流传于民间的古老拼板玩具． 它取材简单、制作便捷，但又千变万化，充满挑战，内含人类的智慧与文明． 七块板可拼成许多图形(1 600种以上)，例如三角形、平行四边形、不规则多边形，玩家也可以把它拼成各种人物、动物、桥、房、塔等，也可以是一些中、英文字符． 七巧板是中国古代劳动人民的发明，其历史至少可以追溯到公元前一世纪，到了明代基本定型，明、清两代时在中国民间广泛流传．

例4七巧板是一种古老的中国传统智力玩具，它由七块板组成，其简易结构如图5所示． 某人将七巧板拼成如图6中的狐狸形状． 若在七巧板中随机取出一个点，则该点来自于图中阴影部分的概率为( )．

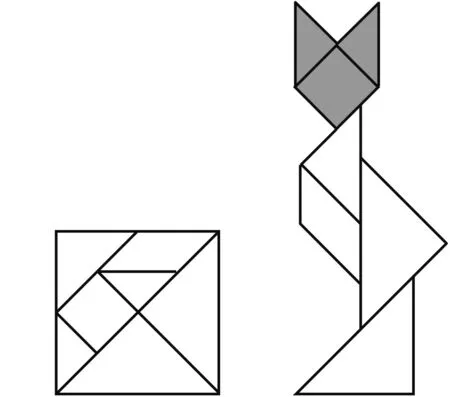
图5 图6

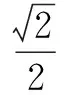
5 中国象棋——楚河汉界自古有，排兵布阵靠统筹

象棋为中国传统棋类益智游戏，与国际象棋及围棋并称世界三大棋类，是中国正式开展的78个体育运动项目之一，也是首届世界智力运动会的正式比赛项目之一． 象棋属于二人对抗性游戏，由于用具简单、趣味性强而成为流行极为广泛的棋艺活动，经国务院批准被列入第二批国家级非物质文化遗产名录．

例5“车走直、马走日、炮打隔子、象飞田、小卒过河赛大车”，这是中国象棋中的部分下棋规则． 其中“马走日”是指马走“日”字的对角线，如图7的棋盘中，马从点A处走出一步，只能到点B或点C或点D或点E． 设马从点A出发，必须经过点M,N(点M,N不考虑先后顺序)到达点P，则至少需走的步数为( )．

图7

A． 5 B． 6 C． 7 D． 8

解析 由图可知，从N到P只需1步，从M到N至少需走2步，从A到M至少需走3步，从A到N至少需走3步． 要使得从点A经过点M,N到点P所走的步数最少，只需从点A先到M，再到N，最后到P，这样走的步数为6． 故选B．

点评本题以中国象棋为背景进行设计，体现了数学文化的教育功能，既可以培养学生热爱数学的情操，又能增强民族自豪感，真正做到了寓教育于考试之中．