基于数学核心素养的教学设计——以“点到直线的距离”为例*

钱建良 谢 丽 (江苏省宜兴市和桥高级中学 214211)

高中数学学科核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六大维度，同时把“能力”内涵进行了拓展，强调了“思维品质”在数学核心素养中的作用． 这些数学核心素养既有独立性，又相互交融，形成了一个有机整体．

我们厘清数学学科核心素养的基本内涵，是为了探索把数学学习内化为能力和品格的有效途径与方法． 今以“点到直线的距离”为例，谈谈基于数学核心素养的教学设计．

1 教学目标

(1)掌握点到直线的距离公式推导中的若干数学思想和方法，掌握公式的简单应用和变式应用，掌握两平行线的距离公式．

(2)形成严谨的思维习惯，体会分类讨论及化归的思想，领会探索新问题的学习策略，提高认知能力和创新能力．

(3)通过创设问题情境，激发创新欲望；通过引导探索，提升创新潜能；通过激活、引申，体验成功喜悦，坚定创新信念．

2 教学设计

2.1 创设问题情境——问题是思维的起点

问题1过一定点P分别作一个角的两边的垂线，所确定的角与已知角有何关系？

启发引导作图1和图2．

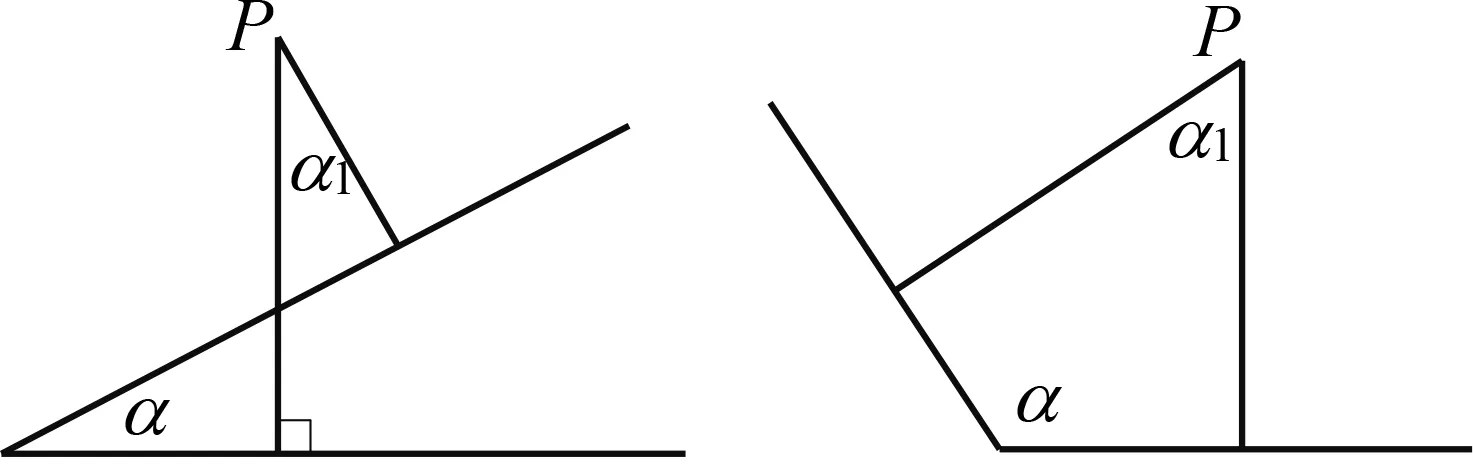
图1 图2

生答：……

设计意图创设问题情境，激发学生解决问题的动机，并为解决问题2作铺垫．

问题2已知点P(x0,y0)和直线l:Ax+By+C=0，怎样求点P到直线l的距离呢？

2.2 启发引导探究——主动探究是解决问题的金钥匙

师：你见到过类似的问题吗？

生：……

师：作垂线→列方程→求垂足→算距离． 书上指出，思路自然，运算量大，真是如此吗？课后你不妨试一试．

师：换个角度考虑，你能解决其中一部分或某些特殊情形吗？

例如，(1)A=0时，d=？(2)B=0时，d=？更一般的问题呢？(3)设A≠0，B≠0，如何化归为一些特殊情形或解决了的某些问题呢？

设计意图用波利亚《怎样解题》中的思想，指导学生探讨，提高学生的认知策略，调动学生认知的主观能动性． 特例是最好的引路人，特例也是分类讨论的出发点，也常常是数学思维活动的切入点．

图3 A≠0，B≠0,d=?

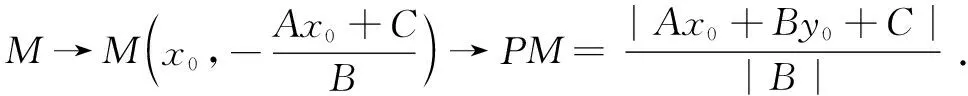
师：求出PM，如何求PQ呢？

引思促思发现，在Rt△PMQ中引进角参数∠MPQ=α1，对照问题1进行类比可发现α1与倾斜角α有何关系？

说明(1)公式的特征，分母：勾股定理的影子；分子：当P(x0,y0)在直线l上时，d=0，即P在直线l上⟺d=0(证明点在直线上)；(2)应用，需把直线方程化为一般式求之；(3)当A=0或B=0时可不套用公式，直接求出．

设计意图(1)充分暴露思维过程，引出倾斜角作参数，利用问题1作台阶，突破难点，使学生认知的“最近发展区”矛盾得到转化；(2)渗透分类讨论思想：①0°<α<90°，②90°<α<180°，强化三角的应用意识和工具作用．

2.3 类比联想引申——跳一跳，你能有更大的收获

你能由上述推导过程领悟其数学思想进行创新，创造出比课本更优美的解法吗？

设计意图本推导中不需要用到分类讨论思想，只需要用到类比思想，由PM的结构式，直接类比出PN的结构式，实在高明，这也是类比思想的一个重要应用．

2.4 应用激活巩固——小试牛刀，轻松过关

应用1：求点到直线的距离．

设计意图本例中涉及四种形式求点线距，可一一化解，有的用点到直线的距离公式，有的用特例，而有的只需将方程化为一般式即可．

应用2：求两条平行直线间的距离．

问题4求平行直线 3x-4y+6=0和3x-4y-4=0的距离．

师：点拨引导，将其化归为点线距离解决．

2.5 推广拓展延伸——动动手，你能从中体会到数学的乐趣

问题5如何求两平行线l1:Ax+By+C1=0，l2:Ax+By+C2=0(C1≠C2)的距离公式？

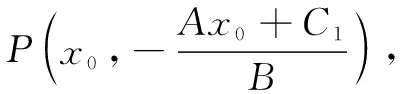
说明本问题解决了两平行线间的距离公式，可直接应用． 但要注意x,y的系数要对应相等． 这也是一个易错点．

2.6 归纳总结提高——提升新境界

唱好“两两两”之歌，点到直线公式轻松过：两个思想——等价转换思想与分类讨论思想；两种应用——直接用，变式用；两项注意——①当心特例，当A=0或B=0时可直接求，②可求两平行线间的距离公式，但要注意x,y的系数要对应相等．

设计意图抓住知识结构和数学思想方法，作归纳总结，点拨提高． 帮助学生产生新旧知识有意义的同化作用，建构新的数学认知结构，从而进入更高一级的数学认知水平．

3 教学感悟

3.1 关注教学设计，在钻研中领会意图

这节课是解析几何中直线部分的一节经典课． 教学设计中采用问题探究教学模式，关注学生学习的过程，重视数学课堂文化建设(互动探究文化、数学交流的文化、课堂对话的文化)． 教学设计中，围绕本节课的教学任务有三大项：点到直线的距离公式的推导，点线距公式的应用，两平行直线的距离． 学生的思维活动也对应三个阶段：一是公式推导，充分挖掘教材资源，引导学生用波利亚《怎样解题》中的思想，指导学生探讨，提高学生认知策略，调动学生认知的主观能动性；二是公式应用，在四种情形下去应用公式；三是推广拓展延伸，解决了两平行线间的距离公式． 这样循序渐进化解难点，既体现出化归思想的充分应用，又符合学生的认知规律． 营造了课始兴趣生、课中兴趣浓、课后兴犹存的愉悦探究氛围．

3.2 关注学生发展，在活动中发展思维

本节课突出了学生的主体地位，发展学生的认知力，教学生学会思考，体会教学内容的本质，始终把培养学生的创造性思维能力和解决实际的能力放在首位． 例如，提出问题2：已知点P(x0,y0)和直线l:Ax+By+C=0，怎样求点P到直线l的距离呢？教师启发学生思考：换个角度考虑，你能解决其中一部分或某些特殊情形吗？例如，(1)A=0时，d=？(2)B=0时，d=？更一般的问题呢？(3)设A≠0，B≠0，如何化归为一些特殊情形或解决了的某些问题呢？特例是最好的引路人，特例也是分类讨论的出发点，也常常是数学思维活动的切入点． 充分暴露思维过程，突破难点，使学生认知的“最近发展区”矛盾得到转化． 问题2解决后，接着又引导学生进行类比联想引伸，领悟其推导过程中的数学思想，并创造出比课本更优美的解法，也就是点到直线距离公式的第2种推导方法． 本节课通过合作探究、师生互动，展示知识的发生过程，使学生逐步体会和感悟从形到数的发展过程，展现了解析几何中数形结合的本质，暴露了数学家原始的思维轨迹，激活了学生的思维，实现了教师以启为导，学生因思而悟来完成教学目标．

3.3 关注核心素养，在探究中享受数学

最近三年有关“数学核心素养”的课题备受瞩目，对数学核心素养的研究和讨论成为了教育的热点． 数学教师在课堂教学中不能单纯地讲数学或让学生一味做练习，而是应引导学生在“用数学”中实现核心素养的内化提升． 这里说的“用数学”，主要是指“用数学眼光观察世界，用数学思维思考世界，用数学语言表达世界”三个方面． 在课程改革深入推进的今天，数学课堂教学要注意挖掘人文教育内容，重视数学的人文性，使数学的人文精神价值得到进一步扩展，并以此加强对学生数学核心素养的培养，更新学生的世界观和方法论． 今天，学生获得数学知识的渠道变了，要在经历、探究学习过程中，获得基础知识和基本技能，并能解决一些实际问题；学生获得的数学知识的形态变了，要在自己动手实践“做数学”的过程中，建构数学知识的意义，获得数学活动的经验． 因此在当前的新课程改革中，为了使新课程真正适应学生的发展，对于数学教师来说，在教学实践中关注学生的核心素养的培养，重视数学课堂文化的建设，应用问题探究的教学模式就显得尤为重要．