几何画板在初三专题复习课中的应用——以“二次函数图象”为例*

冯 伟 (江苏省苏州市景范中学校 215000)

张 骅 (江苏省苏州市第一初级中学校 215000)

《义务教育数学课程标准(2011年版)》指出：“信息技术的发展对数学教育的价值、目标、内容以及教学方式产生了很大的影响． 数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的整合，注重实效． 要充分考虑信息技术对数学学习内容和方式的影响，开发并向学生提供丰富的学习资源，把现代信息技术作为学习数学和解决问题的有力工具，有效地改进教与学的方式，使学生乐意并有可能投入到现实的、探索性的数学活动中去． ”[1]如何在数学教学中应用信息技术?经过多年的探索和实践，我们认为几何画板是一个很好的平台．

本文以一节关于含参二次函数的区级公开课为例，谈谈在教学中如何通过合理运用几何画板提升学生的数学思维能力．

1 教学片断

题目已知二次函数y=m(x2-6x+8)(m为大于0的常数).

师：请同学们仔细研究二次函数的解析式，思考这个函数的图象有什么特点.

生1：我发现二次项系数大于0，所以抛物线的开口向上．

师：很好，还能发现什么？

生2：我把括号里面的式子进行因式分解，得到y=m(x-2)(x-4)，当y=0时，x=2或4，所以这条抛物线与x轴的交点为(2,0),(4,0)．

生3：根据这条抛物线与x轴的交点为(2,0),(4,0)，我们可以知道抛物线的对称轴是直线x=3．

师：大家回答得非常好，现在我们借助于几何画板把这条抛物线画出来．

操作作直线l∥y轴，点M为直线l上且在x轴上方的任意一点，度量点M的纵坐标m，利用m的值作出函数y=m(x2-6x+8)的图象，交x轴于点A、点B，交y轴于点C，拖动点M的时候，函数图象也随之变化，可以发现，抛物线在运动的过程中经过定点A,B(图1)．

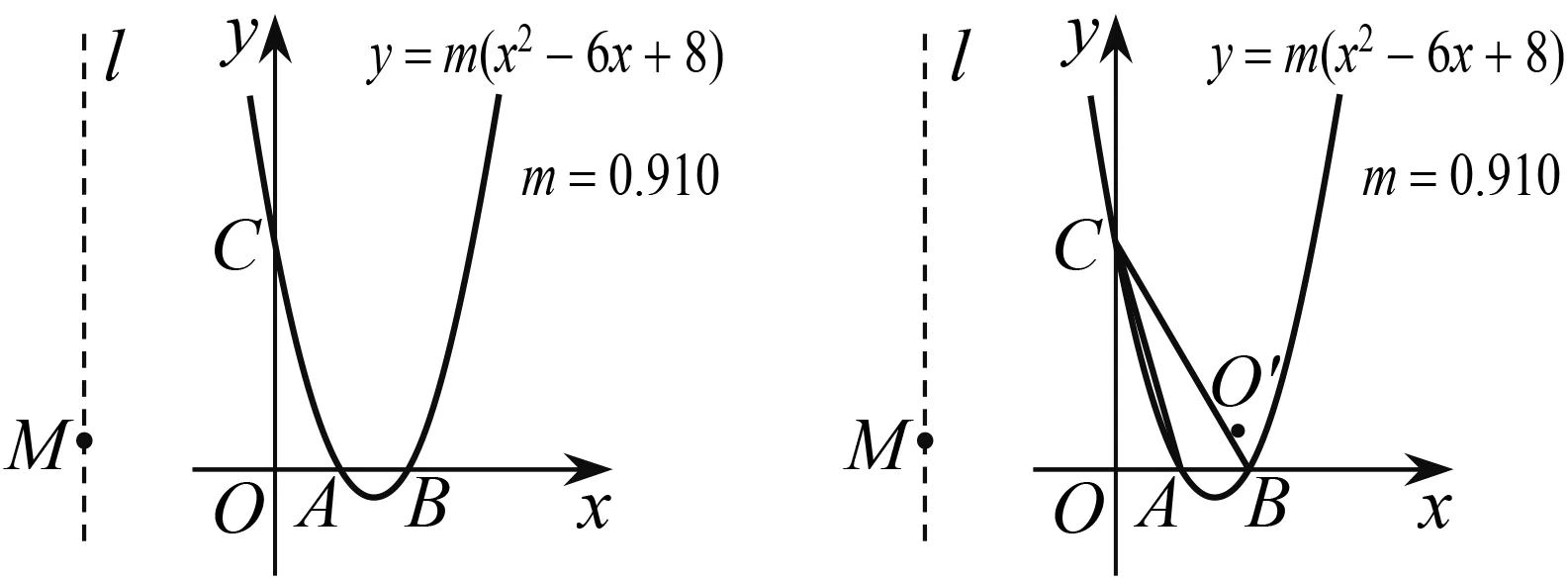
图1 图2

问题1以AC为对称轴，将原点O反射得到点O′(图2)，请同学们仔细观察，已知点O和点O′关于直线AC成轴对称关系，当拖动点M的时候，点O′能否落在线段BC上？

生4：我发现拖动点M的时候，点O′在移动，但是一直到不了线段BC上，但不知道为什么．

生5：可以假设O′能落在线段BC上，根据现有的条件，AC平分∠OCB，那点A到BC的距离就和AO相等，应该等于2，但AB也等于2，那就矛盾了！所以不管点M如何移动，点O′肯定不能落在线段BC上．

师：回答得非常好，下面我们继续调整点M的位置．

问题2继续以AC为对称轴，将原点O反射得到点O′，作出抛物线的对称轴，交x轴于点D，拖动点M． 请同学们观察，如果点O′落在抛物线的对称轴上(图3)，那么此时m的值是多少呢？

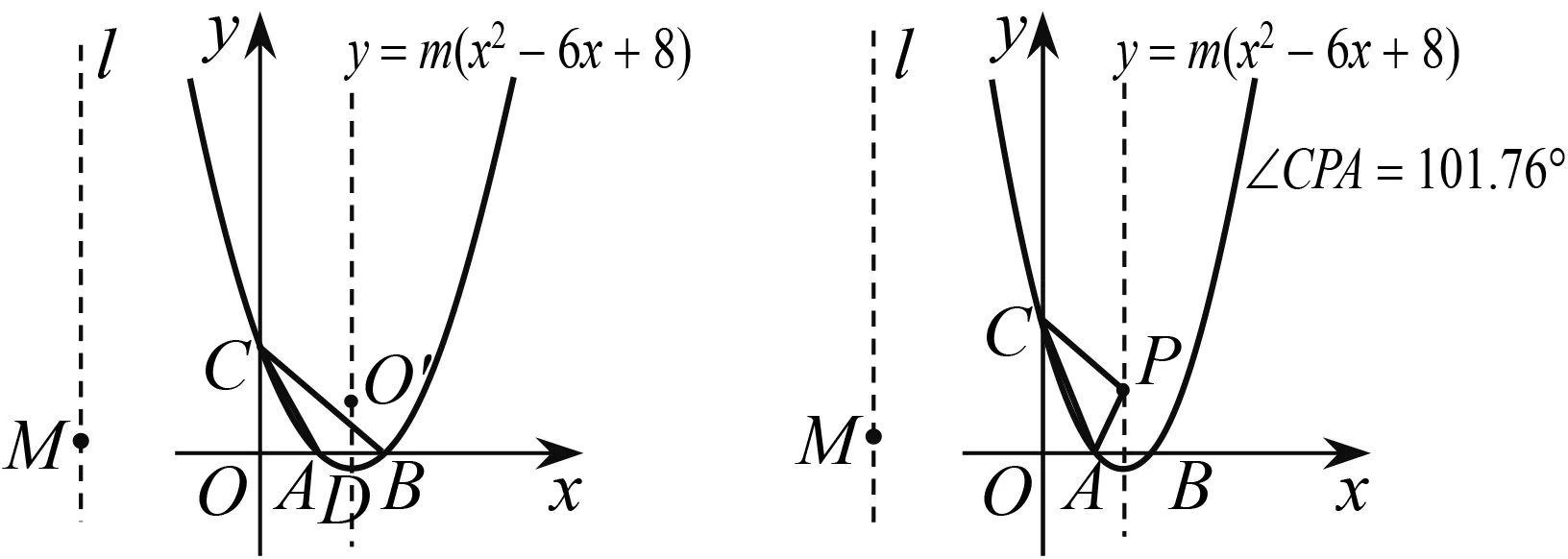
图3 图4

问题3在抛物线对称轴上任取一点P，连结PC,PA，拖动点P，度量出∠CPA的度数． 请同学们观察(图4)，现在∠CPA是一个钝角，当拖动点P向上或向下的时候，∠CPA的度数会变小，显然，在∠CPA的度数变小的过程中，∠CPA在某个时刻会成为直角，而且将P往上移动和往下移动都会使得∠CPA成为直角，也就是说∠CPA有两次成为直角的机会． 但是，当拖动点M后，∠CPA最大也没有达到直角，看来∠CPA的值和m是有密切关系的，请问：m的值满足什么条件会使得∠CPA能够两次成为直角？

生：……(陷入思考中)

生6：老师，我有一个方法，你可以作以AC为直径的圆吗？

教师据此作出圆，圆心为点Q．

生7：以线段AC为直径的圆只要和抛物线的对称轴有交点，根据直径所对的圆周角为直角可以知道交点就是直角的顶点，要满足题目的要求，只要拖动点M，使这个圆和抛物线对称轴有两个交点就可以了．

师：你这个方法很奇妙，老师备课的时候也没有想到，现在我们要求m的范围，应该怎么办呢？

生(有人插话)：只要圆和对称轴相切就好了．

教师拖动点M，使得圆Q和抛物线对称轴相切(图5)．

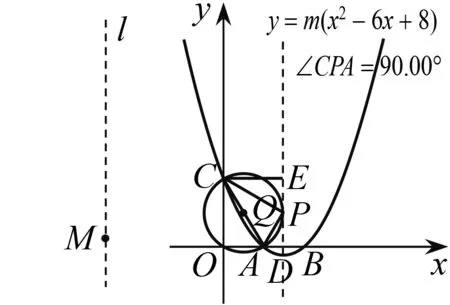
图5

生6：只要求出圆Q和对称轴相切时m的值，然后大于这个值就是要求的范围．

师：那怎么求出这个值呢？

2 思考

(1)在专题复习课中适当地运用几何画板可以提升复习的效率

初三数学二轮复习通常以专题复习为主． 从学生学习的角度来看，专题复习所起的作用在于用专题的方式强化学生对某一种或某一类题型的认识，强化对某一块数学知识或某个数学方法运用的熟练程度． 本文涉及的课题是二次函数的图象，所设计的问题都和动点有关，问题的难点体现在和函数图象相关的几何性质上． 而几何画板不仅能够精准地展现几何图形，还能够动态地再现数学图形和问题的整个演变过程，并且在动态演示中保持其图形几何性质的稳定，帮助学生发现隐藏在图形变化后面不变的几何规律，触及问题的数学本质．

本课全部的问题都围绕同一个二次函数图象展开，函数图象是一条随着m值的变化而变化的抛物线． 怎样在课堂中动态呈现，并且在抛物线变化中保持一些性质不变(比如与x轴的交点、对称轴等)，这些要求通过运用几何画板可以得到很好的实现(拖动动点M)． 在绘制二次函数图象时，没有直接建立一个参数m(直接建立的参数的变化不是平滑和连续的，而是离散和跳跃的)，而是通过度量一个点M的纵坐标来体现参数m取值的任意性，而且学生也很容易理解点M的位置(主要是上下方向)和m的值一一对应，通过上下拖动点M从而使得函数图象随之发生改变．

在问题1中，原本设计的问题是问线段AC能否平分∠OCB，如果可以，求出m的值；如果不可以，说明理由． 但是在一个班级试上后发现，提出问题后学生思考不活跃，再与备课组老师共同研讨，决定在这个问题上充分利用几何画板的动态性，将原点O沿AC反射，问反射点O′能否落在BC上． 这样的处理增加了学生思考的逻辑容量，而且在课堂上通过直接操作几何画板动态展示问题，能够激发学生研究问题的兴趣．

而在难度比较大的问题3中，通过几何画板拖动点P和点M，实时度量∠CPA的度数，可以使学生直观地感受到点P运动过程中∠CPA能否成为直角是由点M的位置，即m的值决定的，从而化解了学生审题的难度．

(2)运用几何画板要跳出常规多媒体课件制作和播放的窠臼

课件的设计是教师依据学生对这堂课的学习需求进行分析后提出的解决问题的最佳方案，是使教学效果达到优化的系统决策过程，是教师主导作用的事前体现． 在传统的课堂教学中，很多教师采用预先做好课件，在课堂进行“播放”的模式，这要求教师在课前尽量预设好课堂中所有的情况． 但实际上，由于学生的知识结构和学习能力存在差异，教师不可能预见实际学习进程中的各种情况或变化(相信每一位数学教师都会遇到学生的思考思路和自己的备课不一致而自己制作的课件又无法及时跟进这种尴尬的情况)． 比如在问题3中，生6的解答非常精彩，而教师在备课中对这个问题的解答主要是使用代数方程求根解决，对于生6的解法没有预想到，属于课堂教学突发情况． 这时，如果采用其他的多媒体技术，比如PPT，显然就无法应对了． 但几何画板的易操作性使教师在课堂上能够实时修改或完善课件，甚至在课堂教学中由教师根据学生的学习情况当场制作，动态生成． 事实上，实时观看教师的作图过程，有助于学生更好地理解教师讲授的内容或课件制作中所蕴含的数学原理．

3 结语

专题复习是初中数学二轮复习的主要形式，通过一个个专题的处理，将学生在第一轮复习中的双基巩固工作推至高潮，内化为他们的能力． 在此过程中，恰当地使用几何画板有助于拓宽学生分析和解决问题的思路，化解综合动态题的难度，进而提高复习课的效率．