分裂可行问题自适应步长惯性球松弛CQ算法
张雅轩,张亚龙
(中国民航大学理学院,天津 300300)
分裂可行性问题是指找一点x*,满足x*∈C,Ax*∈Q,其中,C 和Q 分别是Hilbert 空间H1和H2中的非空闭凸子集,A 是H1→H2的有界线性算子。该问题首次由Censor 等[1]在有限维Hilbert 空间中提出,且得到了广泛应用。近年来,许多学者提出了求解分裂可行性问题的迭代算法,其中,被广泛关注的一种是Byrne[2]提出的CQ 算法。但在算法实现中,一般闭凸子集上的投影不易计算,确定步长取值范围的算子范数也难于估计。针对第一个问题,Yang[3]提出了半空间松弛CQ 算法,Yu 等[4]提出了另一种用闭球进行松弛的CQ 算法。针对第二个问题,López 等[5]提出用自适应步长代替算法中的固定步长,Qu 等[6]将Armijo 线搜索用于分裂可行问题CQ 算法的步长设计。近年来惯性加速算法大量涌现,对算法收敛速度的提升效果明显。Polyak[7]首次从微分方程角度提出惯性项,并将其用于光滑凸优化问题求解加速,但没有涉及惯性项在分裂可行性问题中的应用。综上所述,在经典CQ 算法基础上,采用自适应步长及球松弛方法,并引入惯性项构造新算法,用于求解分裂可行性问题,可有效加快算法的收敛速度。最后证明算法在无限维Hilbert 空间中强收敛。
1 预备知识
设H 是一个Hilbert 空间,称T ∶H→H 为firmly非扩张映像,如果∀x,y∈H

其中,T 为firmly 非扩张映像当且仅当I-T 也为firmly 非扩张映像。
设C 为H 中的非空闭凸子集,定义度量投影算子PC:H→C 为
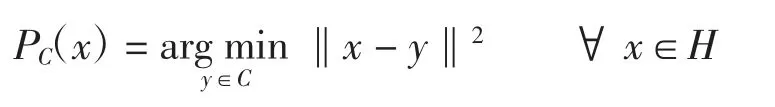
投影算子为firmly 非扩张映像。
引理1[8]设数列{sn}和{cn}为非负实数列,满足

其中:{an}⊂(0,1);{cn}为实数列。假定则①如果bn≤anM(M>0),则{sn}有界;②如果且则
引理2[9]设{sn}为非负实数列,满足
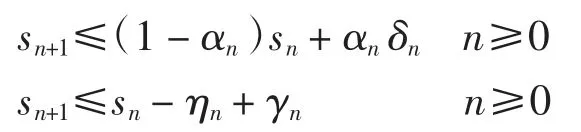
其中:{αn}⊂(0,1);{ηn}是非负实数列。若{αn}、{ηn}和{γn}满足:蕴含则有
2 算法及其强收敛性
假设集合C={x∈H1| c(x)≤0},集合Q={y∈H2| q(y)≤0},其中,c:H1→(-∞,+∞],q:H2→(-∞,+∞]为下半连续的强凸函数。定义
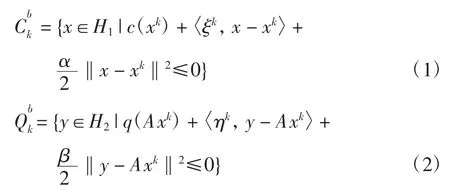
其中:ξk∈∂c(xk);ηk∈∂q(Axk)。如果c 和q 分别为α-强凸函数和β-强凸函数,可证明和为分别包含C,Q 的闭球[4]。
进一步假定H1:分裂可行性问题的解集用S 表示且非空,H2:c 和q 的次微分在有界集上有界。记
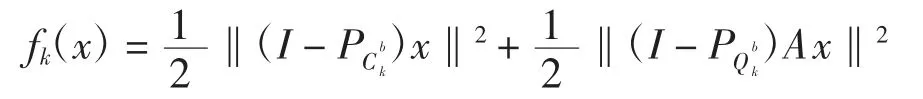
算法1任取u,x0,x1,假设αk∈(0,1),βk∈(0,1),有


定理1若:其中,β∈[0,1),‖xk-xk-1‖=0,则{xk}强收敛于PSu。
证明设x*=PSu,由I-与I-是firmly 非扩张映像,可得

则由式(3)及算法1 中λk的定义,有

由算法1 可知0<ρk<4,则

由式(5)和式(6)有

其中

由定理1 中条件③及引理1 中①表明,数列{xk}、{yk}、{Δfk(yk)}都有界。
另一方面


结合式(4)可得

综合式(7)和式(8)可得

令

则式(9)可重写为

根据引理2 及定理1 的条件②和③,要证明{xk}强收敛,只需证明蕴含


同理可知

根据投影算子的性质,有

另一方面,由定理1 的条件③,有
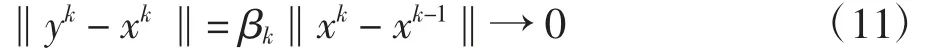
从而有
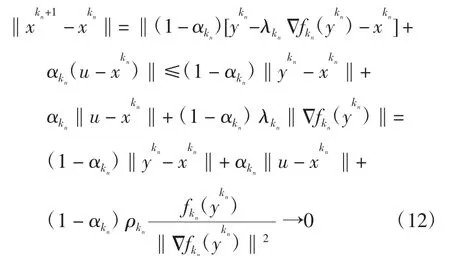
由式(10)、(11)和(12)可得
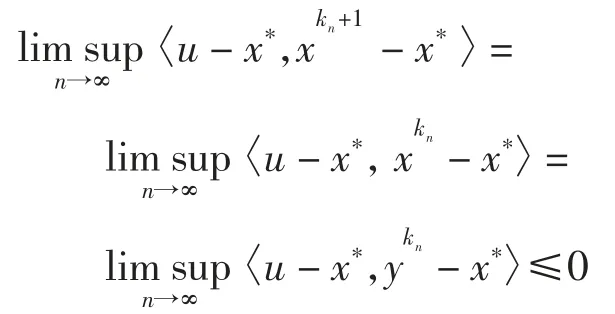
证毕。
3 结语
针对分裂可行性问题,在有限维空间中自适应步长的球松弛CQ 算法基础上,添加了惯性项加快收敛速度;同时利用Halpern 迭代格式调整算法。最后,证明算法在无限维Hilbert 空间中强收敛。

