基于飞行轨迹的离场航空器噪声计算方法
王 超,郝铭飞
(中国民航大学空中交通管理学院,天津 300300)
机场噪声严重影响周边人群的工作和生活,已经成为全球性难题。掌握机场噪声数据,是进行机场规划的基础。目前,监测机场噪声主要采用基于传感器的实地监测法。实地监测法有两大缺陷:一是受地貌环境等影响,监测点布局不够灵活;二是测量结果不能区别出飞机噪声与环境背景噪声,不能准确评估飞机噪声的影响。因此,摆脱监测环境影响、准确评估机场噪声具有重要意义。
目前,除了基于传感器的实地噪声监测法,在飞机噪声评估方面的研究主要有:国外,以噪声-推力-距离(NPD,noise-power-distance)曲线为核心,研究开发了相关的噪声评估模型,如美国联邦航空管理局的综合噪声模型(INM,integrated noise model)[1],美国国防部提出的高级声学模型(AAM,advanced acoustic model)[2]和日本的机场噪声模型(JCAB model)[3];国内,姚飞[4]采用波音爬升程序(BCOP,boeing climb out program)预测飞行航迹,然后使用噪声环评助手EIAN2.0评估噪声;王超[5]根据标准离场程序的推力进行航段匹配,并提出等效稳定航段推力的概念,通过对NPD数据插值计算飞机噪声;高垒等[6]采用航段分割法分别基于当前航班信息及预测的飞行流量评估机场噪声影响。现有对航空器噪声的评估方法,均是在已知航空器推力信息基础上,结合飞行轨迹对噪声进行计算。目前,虽有多种陆基设备可以获取航空器轨迹数据,但获取的轨迹数据通常不含航空器推力信息,准确的推力信息较难获得。
飞行轨迹作为飞机操作程序的直观体现,间接反映了航空器所用的飞行程序和垂直剖面管理程序。以离场为例,分析飞机噪声和性能(ANP,aircraft noise and performance)数据库中的离场垂直剖面,根据飞行轨迹确定所用离场垂直剖面管理程序,结合程序中的推力信息与飞行轨迹计算飞机的噪声影响。
1 飞行轨迹航段划分
基于NPD 数据及飞行轨迹评价航空器噪声时,由于NPD 数据中的噪声数据是基于航空器在无限长航线上保持直线飞行的假设条件,为利用NPD 中的噪声数据,需要将实际弯曲的飞行轨迹划分成一系列相邻的直线段,对每个直线段进行NPD 数据插值。根据轨迹剖面的特点,采用改进的Douglas-Peucker 算法提取轨迹水平剖面和垂直剖面的特征点,以轨迹特征点将弯曲的、爬升率不同的飞行轨迹划分为若干直线航段。
1.1 轨迹剖面分析
航空器按照飞机操作程序飞行时,受导航设施、人为因素等影响,飞行轨迹总会与预设路径产生偏差。飞行轨迹是飞机在一系列连续时刻的空间位置,定义一条轨迹中轨迹点pi=(ti,xi,yi,hi,vi,φi),其中,i 为轨迹点编号,t 为轨迹点记录时间,x 为轨迹点的横坐标,y 为轨迹点的纵坐标,h 为轨迹点的飞行高度,v 为轨迹点的表速,φ 为轨迹点处的航向,则一条飞行轨迹可表示为T=(p1,p2,…,pi,…)。
从空间上,根据飞行轨迹的三维形状可将其分解为水平轨迹和垂直轨迹。水平轨迹由一系列直线飞行段和圆弧飞行段组合而成,根据转弯情况,可分为直行、左转和右转,如图1所示。垂直轨迹是飞行轨迹在地面直角坐标系垂直面上的投影,表征了飞机飞行过程中垂直方向的机动飞行情况。飞机在垂直平面内的运动由垂直剖面管理程序决定。在标准离场中,根据离场爬升类型的不同可分为加速滑跑段、加速爬升段、等表速爬升段、平飞加速段和等马赫数爬升段等,如图2所示(1 ft=0.304 8 m)。
1.2 改进Douglas-Peucker 算法的轨迹特征点提取
Douglas-Peucker 算法[7-8]是一种对大量冗余数据点进行压缩,提取必要数据点的抽稀算法。该算法简化轨迹数据时能够保持轨迹的大致轮廓,使用Douglas-Peucker 算法提取特征点的思路如下:①给定数据简化的限差d0;②连接曲线首尾两点A、B 形成一条直线段,找到曲线上离该直线段距离最大的点C,计算其垂直距离d;③比较垂距d 与给定限差d0,如果d>d0,则将曲线分为AC 和CB 两段,并分别对两段曲线重复步骤②~③,直到新曲线段中的最大垂距d<d0,曲线被简化完毕;④当所有曲线段都处理完毕后,依次连接各分割点形成折线,作为原曲线的近似,所有分割点即为曲线的特征点。
使用Douglas-Peucker 算法提取特征点时,由于该算法提取了所有变化超过一定幅度的点,而这些特征点包含且不限于轨迹转弯模式改变点和爬升率发生变化点。为了准确提取飞行中的转弯点、爬升率变化点,分别从轨迹水平剖面和垂直剖面提取特征点。
提取轨迹水平剖面特征点时,以轨迹在地面的投影坐标作为轨迹,记轨迹端点为A1(x1,y1)、B1(x2,y2),则轨迹上任一点O1(x0,y0)到线段A1B1的垂直距离表示如下


图1 轨迹水平剖面Fig.1 Horizontal profile of trajectory

图2 标准离场爬升阶段划分Fig.2 Standard departure climb phase division
提取轨迹垂直剖面特征点时,为了获取爬升率发生变化的点,以时间-高度记录轨迹。由于时间t 与高度h 量纲不同,飞机轨迹垂直剖面变化不满足单位时间内上升或下降单位高度,故引入修正系数α、β。记轨迹端点为A2(t1,h1)、B2(t2,h2),则轨迹上任一点O2(t,h)到线段A2B2的垂直距离表示如下

2 航段推力估算
分析ANP 数据库可知,离场垂直剖面管理程序考虑10 000 ft 以下的爬升,前后相邻航段的爬升类型不直接相关。在离场过程中,推力由最大起飞推力改为最大爬升推力,且襟翼角度从大逐渐变小,直至收上襟翼(零襟翼)。以空客A320 飞机为例,离场垂直剖面管理程序中前后相邻航段的飞机推力、襟翼关系如表1所示。

表1 程序中推力和襟翼设置规律Tab.1 Thrust and flap setting rule in procedure
2.1 垂直剖面管理程序确定
借鉴可行解概念定义:满足相邻航段间飞机状态变化规律的垂直剖面管理程序为可行垂直剖面管理程序,如ANP 数据库中提供的DEFAULT 程序、ICAOA程序与ICAOB 程序。在实际飞行中,管制员对飞行轨迹影响较大,因此,衍生出更多的垂直剖面管理程序,按照可行垂直剖面管理程序飞行生成的垂直轨迹即为可行垂直轨迹。
根据垂直轨迹确定垂直剖面管理程序时,按照可行垂直剖面管理程序计算出所有可行垂直轨迹,认为与实际垂直轨迹最接近的可行垂直轨迹为实际垂直轨迹的标称垂直轨迹(图3),生成标称垂直轨迹的垂直剖面管理程序为实际垂直轨迹所对应的垂直剖面管理程序。
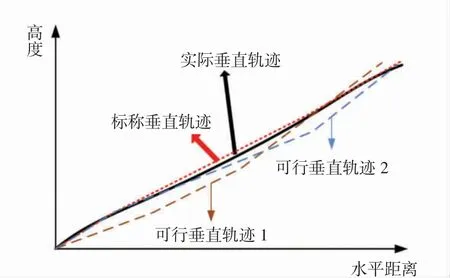
图3 可行垂直轨迹与标称垂直轨迹剖面Fig.3 Profiles of feasible and nominal vertical trajectories
由于飞行轨迹的连续性,顺序计算各段剖面时,前航段的终点即为后航段的起点。默认离场第1 个轨迹段对应的垂直剖面管理程序与标准离场垂直剖面管理程序首段一致,从第2 航段起,按照前后相邻航段的爬升类型、推力、襟翼变化规律,可计算航段可行垂直轨迹。
假设机场风速不超过15 kt(1 kt=1.852 km·h-1),忽略起飞离场时飞机的重量变化。在某一航段内,当飞机按照等表速爬升时,根据实际轨迹段终点的高度、速度等参数计算可行垂直轨迹[9],即
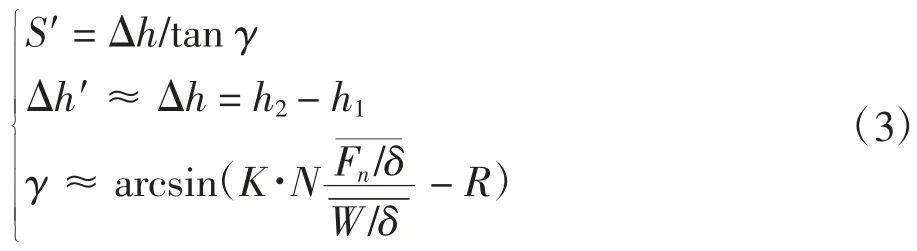
其中:S′为可行垂直轨迹段的水平距离;Δh′为可行垂直轨迹段的高度增量,Δh 为实际垂直轨迹段的高度增量;h1,h2为轨迹段起点和末点的高度;γ 为平均爬升角;K 为速度相关常量,当校正空速VC≤200 kt 时,K取1.01,否则,K 取0.95;N 为发动机数量;为航段平均修正净推力;W 为飞机重量;δ 为气压比;R 为飞机阻力系数与升力系数的比值,与襟翼角度有关。
当飞机加速爬升时,根据实际轨迹段的平均爬升率等参数计算可行垂直轨迹[9],即
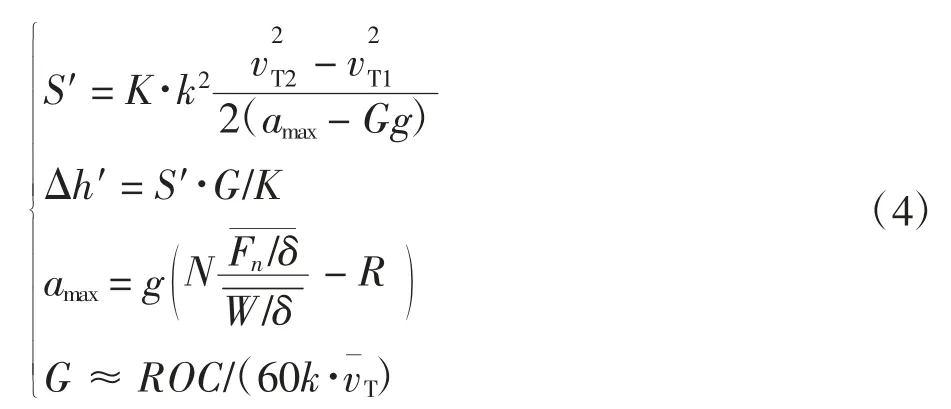
其中:k 为单位转换常数;vT2、vT1为航段终点与起点的真空速;为航段平均真空速;amax为平飞最大加速度;G 为爬升梯度,g 为重力加速度;ROC 为爬升率。
可行垂直轨迹与实际垂直轨迹的偏差可表示为

其中:∑S、∑S′为实际垂直轨迹和可行垂直轨迹所有航段的总水平距离;∑Δh、∑Δh′为实际垂直轨迹和可行垂直轨迹所有航段的总高度增量。
2.2 航段推力计算
在确定轨迹离场垂直剖面管理程序的基础上,基于离场垂直剖面管理程序中推力类型及ANP 数据库中的相关参数,可计算出轨迹点单发净推力[9]为

其中:h 为飞机高度;E、F、GA、GB、H 为发动机推力相关常量,可从ANP 数据库获取;T 为飞机所处环境温度。
由于NPD 数据库中假设发动机保持恒定推力,而实际飞行中,推力总是随高度、推力类型的变化而变化,因此,对飞行轨迹中每个航段需要计算航段等效稳定推力。
假设推力沿航段前进方向呈线性变化,航段起点推力为F1,航段终点推力为F2,则在一小段轨迹航段中,可保守认为航段上最靠近观测者位置的推力为航段推力P,计算如下

其中:q 为航段起点与观测点至航段连线的垂足的距离,当观测点在航段后方时取负值;λ 为航段长度。
3 航空器噪声计算
单事件噪声评价时,有两类评价指标:基于噪度的有效感觉噪声级EPNL、最大感觉噪声级PNLmax和基于响度的A 声级LA、最大A 声级LAmax。声暴露级(SEL,sound exposure level)是在规定测量时间内或对某一独立噪声事件,将其声音能量等效为1 s 作用时间的A 声级[10],既考虑了事件噪声强度又考虑了事件持续时间,能如实反映被测事件的真实能量。
基于分割后的轨迹计算航空器噪声时,对每个简化为直线段的航段,需计算与噪声监测点位置间的斜距,并采用2.2 节方法计算轨迹航段等效稳定推力,然后对已确定机型的NPD 数据插值,计算各航段对噪声监测点的声暴露级SEL。记航段i 对监测点的噪声影响为LAE,i,其插值计算如下
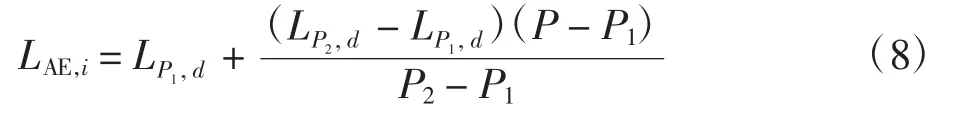
其中
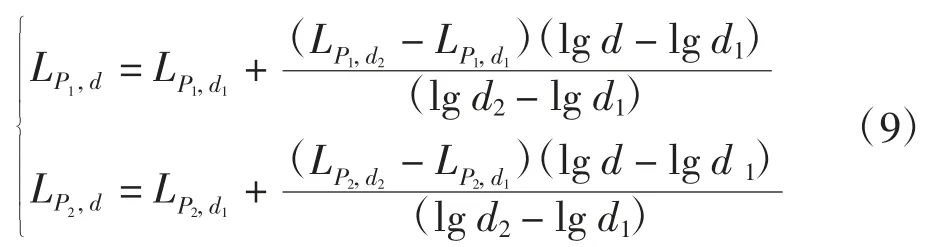
P1、P2为NDP 数据库中可用的推力值;P 为航段i 上航空器的等效稳定推力;LP1,d1、LP2,d1、LP1,d2、LP2,d2为NDP 数据库中可用噪声值;d1、d2为NDP 数据库中可用的距离值;d 为航段i 与噪声监测点的斜距。
整条轨迹对监测点的噪声影响LAE则是各航段噪声影响的叠加,计算如下
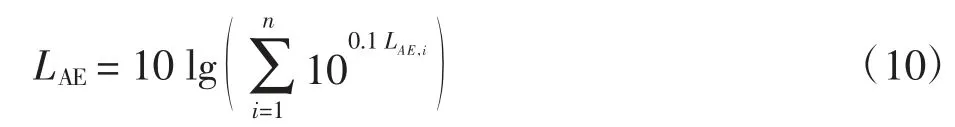
式中,n 为整条轨迹所划分的航段数。
由于噪声影响还受飞行速度、发动机位置及声在空间传播时的衰减等影响,故可根据不同的精度需要,对噪声进行修正,主要包括:速度修正、侧向衰减修正、发动机安装修正及有限长航段修正[9]。
4 实例应用
以天津滨海国际机场34L 跑道、A320-232 机型航班的某条离场轨迹数据为例,飞机起飞重量为65 408 kg。飞行轨迹坐标以天津机场基准点为参考点(即坐标原点),当设置轨迹水平剖面特征点提取限差d1=143 m,垂直剖面特征点提取限差d2=220 ft时,根据特征点划分的轨迹航段如图4所示。

图4 根据特征点划分轨迹航段Fig.4 Trajectory segments divided by feature points
飞机起飞离场过程中,记飞机起飞阶段为TakeOff,等速爬升阶段为Climb,加速爬升阶段为Accelerate;使用推力类型包括最大起飞推力THR-TO 和最大爬升推力THR-C;可使用襟翼设置即最大放出襟翼设为1+F,次之放出襟翼设为1,收襟翼(零襟翼角度)设为0。对所有轨迹航段,在相邻航段间飞机状态变化规律约束下,按照2.1 节方法确定其对应的离场垂直剖面管理程序,离场垂直剖面管理程序中对飞机状态(爬升类型、使用推力类型和襟翼设置)的管理如表2所示。
基于表2中各航段推力设置,可按照式(6)对任意轨迹点计算其瞬时推力;然后根据噪声监测点与航段的位置关系,计算出航段等效稳定推力。
实验选取5 个易受飞机噪声影响的敏感点,包括学校和居民社区。以图4所示轨迹为例,结合噪声敏感点位置信息,根据第2.2 节的推力估算方法和第3节中噪声暴露级计算方法,可确定噪声敏感点(表3)和天津机场周边整体的噪声影响(图5)。为验证该方法的可行性,将计算结果与实地测量法(AWA5680 型多功能声级计)监测结果进行对比。
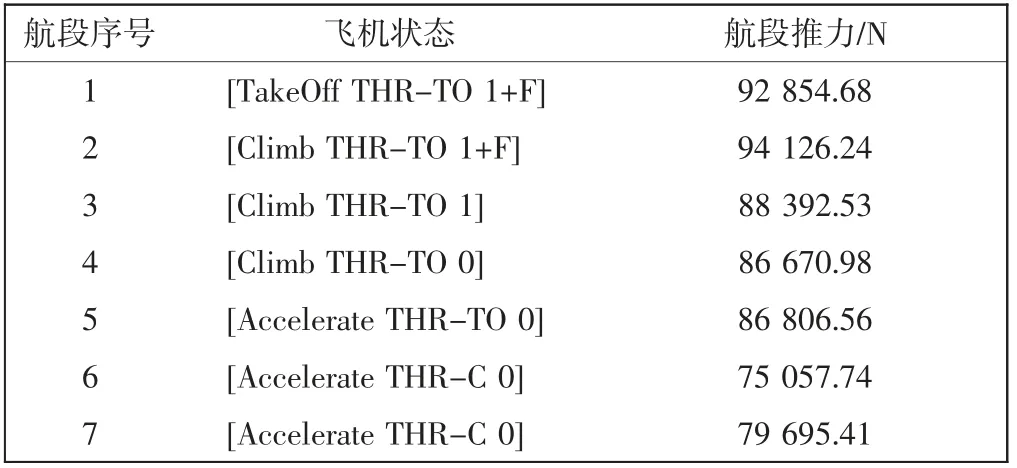
表2 垂直剖面管理程序中飞机状态表Tab.2 Aircraft state in vertical profile managing procedure

表3 噪声敏感点的噪声评估Tab.3 Noise assessment for noise sensitive points
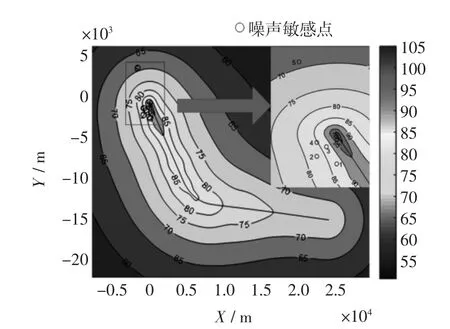
图5 天津机场周边的噪声Fig.5 Noise around TBIA
由表3可看出,基于飞行轨迹计算的噪声结果与噪声实地监测结果相差0.24~1.58 dB,二者比较接近,且基于轨迹的噪声计算结果普遍稍低于噪声实测值,即该方法可行。
5 结语
针对噪声实地监测法受环境影响较大,不能准确评估飞机的噪声影响,而当前基于飞行轨迹评估噪声的相关研究多在已知推力的使用情况下进行评估,因此,提出了一种在推力信息未知情况下,基于轨迹数据计算噪声的方法。以天津滨海国际机场离场的飞行轨迹为例,使用该方法评估了离场噪声的影响,验证了方法的可行性,对完全依赖轨迹数据评价航空器噪声影响具有实际意义。

