带Lévy跳的时滞捕食-食饵随机模型的最优捕获
邱 宏,刘思棋,邓文敏
(中国民航大学理学院,天津 300300)
随着生物数学的不断发展,人们通过建立数学模型对生物种群的生存状况展开研究。1798年,Malthus[1]利用Malthus 种群模型预测了人口数量的增长趋势。19世纪初期,有学者共同建立Lotka-Volterra 模型[2-3]研究种群之间的竞争关系,利用大数律将问题进行简化,从而对确定性模型进行研究。实际上生物会受到随机环境因素的干扰[4-6],因此,确定性模型并不能真实地反映生物的生存状况[7],如:部分地区出现干旱或寒流等现象会在一段时间内抑制当地生物的繁殖,这种对生物产生小程度干扰的因素被称为白噪声[8-10];真实的生态环境中也会出现地震和火山爆发等情况,此类现象被统称为Lévy 跳噪声[11],其特点是概率小,一旦发生便会对周围生物种群产生巨大影响。因此,有学者将这两种环境因素逐渐引入确定性模型中[12-13],开始对生物随机种群模型进行研究。
此外,生物从出生到独立生存会产生时滞效应,Ruan[14]指出时滞会对系统平衡产生影响。将时滞的因素考虑到已有的随机种群模型中,并分析时滞对所研究种群的影响[15-16]。目前,基于单种群和两种群最优捕获策略的研究已取得一定成果[17-18],但关于两生物的种群模型并不足以反映自然界中物种之间的关系,因此,有必要研究在不同环境噪声的影响下,具有时滞的三种群模型的最优捕获问题。
1 研究与方法
1.1 模型构建
为了更加真实反映出自然界中生物种群之间的关系,主要讨论受白噪声和Lévy 跳影响的具有时滞的两捕食者-单食饵的三种群捕食模型。
初始条件:xi(θ)=φi(θ),θ∈[-τ,0],τ=max{τ12,τ13,τ21,τ23,τ31,τ32}。模型表示为
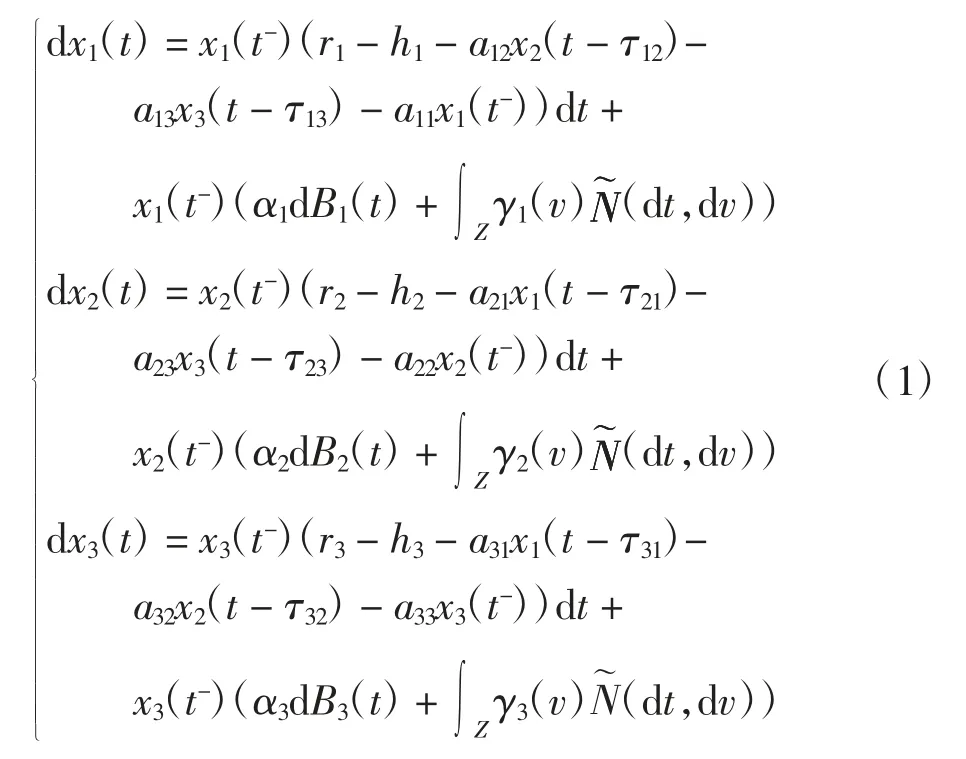
其中:τ 为时滞;φi(θ)为定义在[-τ,0]上的连续函数,φi(θ)>0,i=1,2,3;x1(t)为食饵的种群数量,x2(t)和x3(t)为两捕食者的种群数量,xi(t-)为xi(t)的左极限;hi为xi(t)的捕获努力量,hi>0;ri为xi(t)的增长率,r2,r3<0;aij为物种i 与物种j 间的竞争系数,a21,a31<0(dt,dv)=N(dt,dv)-η(dv)dt,N 为泊松计数测度,η 为N在可测子集Z 上的特征测度且η(Z)<+∞;γ 表示Lévy 跳的影响程度;α 为白噪声强度;B(t)为定义在完备概率空间(Ω,F,P)上标准独立的布朗运动。
1.2 符号说明与假设
从生态意义角度[19]出发,合理假设1+γi(v)>0,v∈Z;考虑到物种的增长率受白噪声影响[20],假设ri→ri+αi(t)。为了便于讨论,定义符号如下
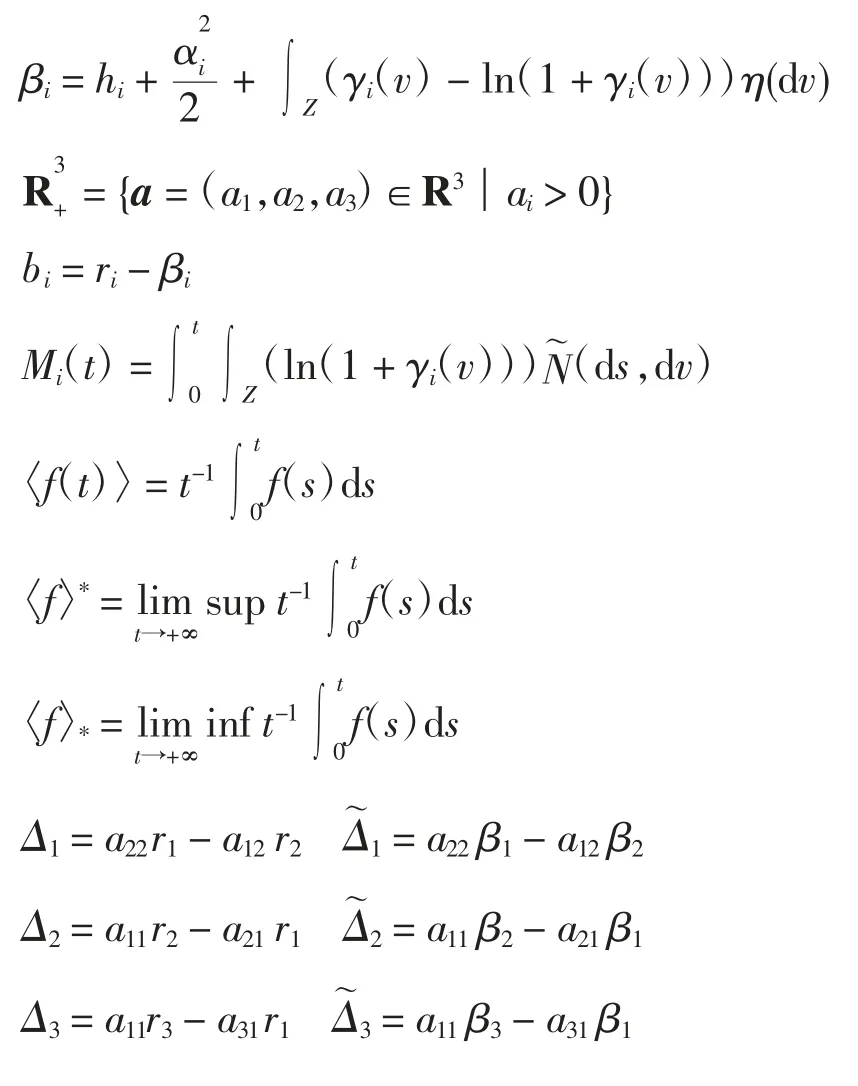

假设1A,A1,A2,A3>0,说明当没有随机扰动时,式(1)有正平衡解[21]。
假设2a11>a12+a13,a22>-a21+a23,a33>-a31+a32[22]。
假设3存在正常数k1,使得 Z∫(ln(1+γi(v)))2×η(dv)<k1,i=1,2,3[23]。
假设4+()T是正定矩阵[23]。
定义1如果则种群x(t)趋于灭绝;如果〈x〉*>0,则种群x(t)在时间平均意义上持久。
引理1任意的初始条件(φ1(θ),φ2(θ),φ3(θ))∈C,式(1)都有唯一几乎确定的全局解x(t)=(x1(t),x(2t),x(3t))T∈,有
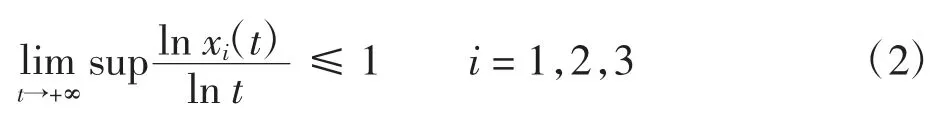
且存在常数k2>0,使得

注引理1 的证明与文献[18]中定理5.1 及文献[19]中定理3.1 相似。
引理2连续函数[24]y(t),有
1)存在正常数T,λ0和λ,使得对所有t≥T,lny(t)≤,则
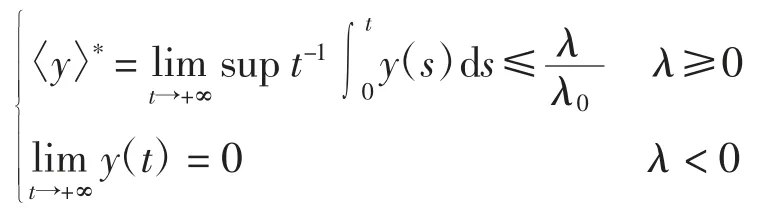
2)存在正常数T,λ0和λ,使得对所有t≥T,lny(t)≥,则
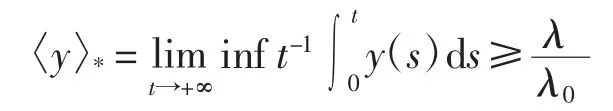
引理3假设{Mt}t≥0是一个消失在时间为0 的局部鞅,则,推出
其中,〈M,M〉(t)是迈耶尖括号过程[25]。
引理4初始条件:mi(θ)=φi(θ),θ∈[-τ,0],τ=max{τ21,τ31},i=1,2,3;令Qi=bi-ai1b1/a11,i=2,3。有如下模型
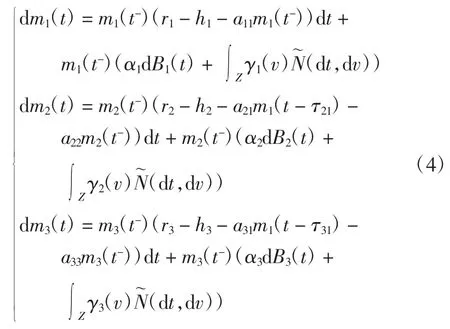
存在:
1)如果b1<0,则
2)如果b1≥0,Q2≥0,Q3≥0,则
3)如果b1≥0,Q2<0,Q3<0,则
4)如果b1≥0,Q2≥0,Q3<0,则
5)如果b1≥0,Q2<0,Q3≥0,则
证明1)对式(4)的一个等式利用伊藤公式,两边同时除以t,可推得
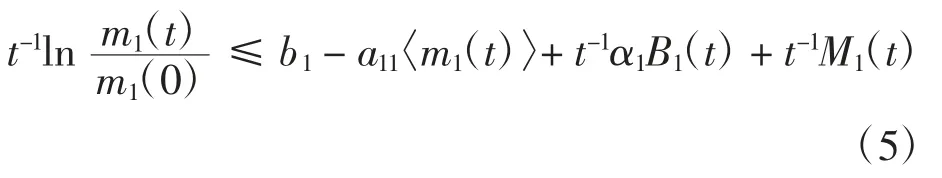

又b2<0,结合伊藤公式,由引理2 及式(6)可知,同理
2)由于b1≥0,根据引理2 及式(5)有

则

计算-t-(1a21ln m(1t)+a11ln m(2t)),由于=0,因此,当Q2,Q3≥0 时,
引理4 中3)~5)的证明与上述相似,省略。
证毕。
注由引理4 知,对1 ≤i ≤3,t→+∞,〈mi(t)〉始终等于一个常数。由于xi(t)≤mi(t),由比较定理[26],对任意的≥0,当t∈[0,τe)时,有

定理1若假设1~假设3 成立,令Γ1=r1/β1,Γ2=则Γ1>Γ2>Γ3。
1)如果Γ1<1,则
2)如果Γ1>1>Γ2,则
3)如果Γ2>1>Γ3,则
4)如果Γ3>1,则2,3。
证明1)由于a21,a31,r2<0,β1,β2,β3,r1>0,则即Γ1>Γ2>Γ3。
对式(1)应用伊藤公式,两边同时除以t,由于a11>0,a12>0,a13>0,则

2)由于Γ2<1<Γ1,由式(10)及引理2 可知,由引理4 中3)可知结合比较定理可得
3)计算(ln m1(t)A13/A33+ln m3(t)-ln m2(t)A23/A33)/t,由式(9)可知,对任意的ε>0,存在T2,使得当t>T2,可推得


计算(A12ln m1(t)/A22-ln m3(t)A32/A22+ln m2(t))/t,当时,令t 充分大,有

即对任意ε>0,存在T3,使得当t>T3时
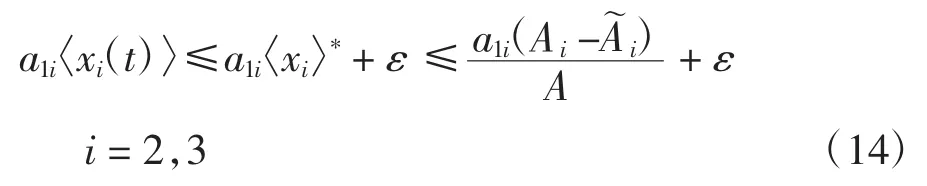
将式(14)代入式(1),可推出

由引理2 可知

同理可得〈x3(t)〉*≥(A3-3)/A,结合式(12)可得,同理可证得

2 依分布稳定性
定理2如果假设2 成立,则式(1)是依分布稳定的[27]。
证明令xi(t)和(t)是式(1)初始值分别为x(θ)和的两个解。ni为第i 个对角元素的余子式,其中

由Kirchioff 矩阵树定理[28]可知,有ni>0,i=1,2,3。令
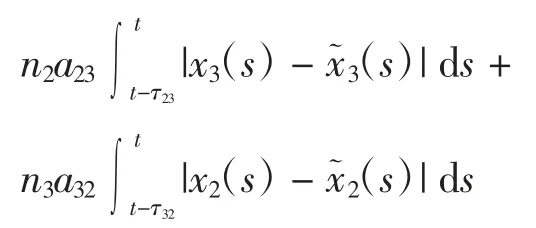
由伊藤公式计算得
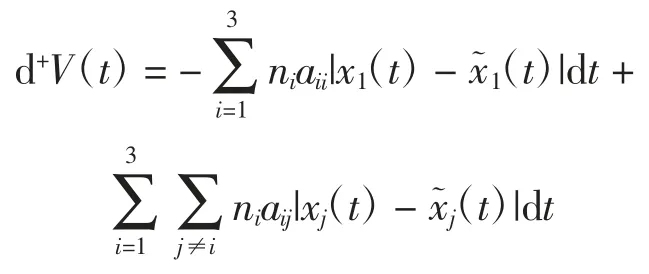
根据文献[29]中定理2.3 可知

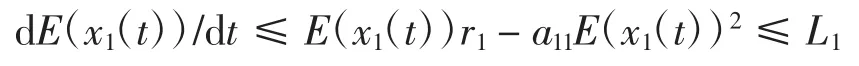
其中,L1为常数且L1>0,则E(x1(t))一致连续。同理,E(x2(t)),E(x3(t))也一致连续。由Barbalat 引理[30]可知

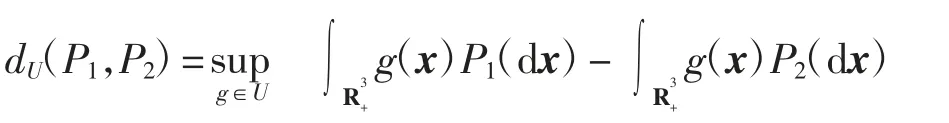
其中,U={g:R3→R|‖g(x1)-g(x2)‖≤‖x1-x2‖,|g(·)|≤1}。对任意g∈U,当t,s>0 时,有

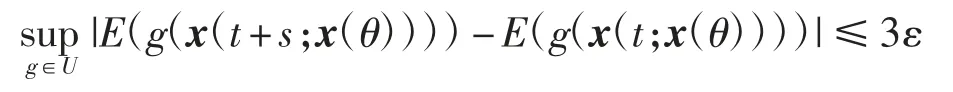
即对任意t ≥T,s>0,有

因此,对任意的x(θ)∈C,{p(t,x(θ),·)| t>0}是空间P 中关于度量dU的柯西列。令ω(θ)≡0,则存在唯一σ(·)∈P(),使得
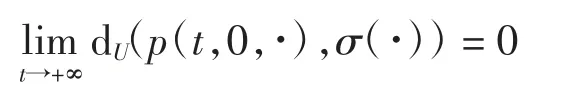
由于式(1)是全局吸引的,则
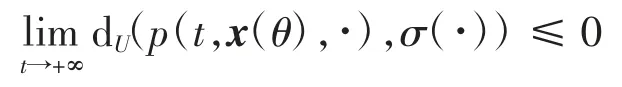
证毕。
3 最优捕获策略
定理3当假设1~假设4 成立时,令

1)如果Γ3|hi=λi>1,λi≥0,i=1,2,3,则OHE 为H*=P,且MESY 为
2)如果1)不能成立,则式(1)不存在最优捕获策略。
证明1)令G={H=({h1,h2,h3)T∈|Γ3>1,hi>0,i=1,2,3}}。由定理1 知,如果H∈G,则定理1 中的4)成立;如果H*存在,则H*∈G,显然P∈G,G 非空。由定理2 知,式(1)有唯一的不变测度φ(·),由文献[18]中定理3.2.6 可知,φ(·)是遍历的,且由文献[31]中定理3.4.3 可知,φ(·)是强混合的。因此,由式(16)知,对任意的H∈G,有
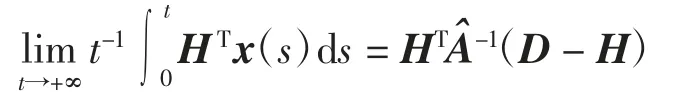
假设P=(λ1,λ2,λ3)T是下列方程

注式(1)中,当γ(·)=0 且τ=0 时,令N=(r1-由定理3 知,OHE 为为
4 结果与分析
令r1=1.6,r2=-0.21,r3=-0.01,A=τ=,A11=4.021,A12=-1.883,A13=-0.069,Δ2=1.267,Δ3=0.471,是正定矩阵,0.001 1。
1)图1表示白噪声对种群最优捕获策略的影响。令γ=(-0.044 1,-0.044 1,-0.044 1)T,图1中α 取值不同时,Y(H*)的平均渐进值结果如下:当α2/2=(0.03,0.09,0.03)T时,=(0.7404,0.3096,0.153)T,Y()=0.701 5;当α2/2=(0.03,0.1,0.03)T时=(0.741 4,0.3042,0.153)T,Y()=0.7007;当α2/2=(0.05,0.1,0.03)T时,=(0.732 4,0.298 1,0.150 8)T,Y()=0.6826;当α2/2=(0.2,0.1,0.04)T时,=(0.664 8,0.252 6,0.129 3)T,Y()=0.5546。
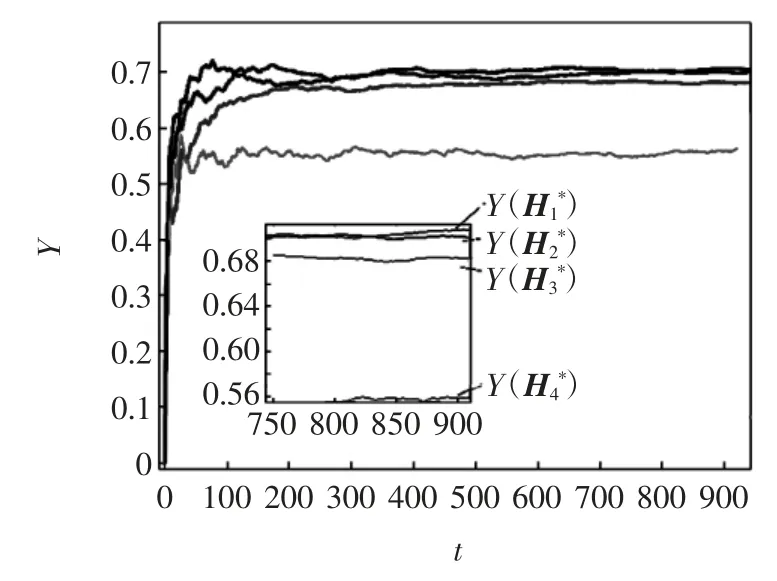
图1 白噪声对最优捕获策略的影响Fig.1 Effects of white noise on optimal harvesting strategy
2)图2表示Lévy 跳噪声对种群最优捕获策略的影响。令α2/2=(0.03,0.10,0.03)T,图2中γ 取值不同时,Y(H*)的平均渐进值结果如下:当γ=(-0.044 1,-0.044 1,-0.044 1)T时=(0.741 4,0.304 2,0.153)T,Y()=0.700 7;当γ=(-0.0441,-0.0755,-0.0441)T时=(0.7416,0.3031,0.153)T,Y()=0.700 5;当γ=(-0.044 1,-0.642 3,-0.428 5)T时=(0.783 4,0.092 7,0.088 8)T,Y()=0.683 8;当γ=(-0.195 3,-0.044 0,-0.044 1)T时=(0.731 9,0.297 8,0.150 7)T,Y()=0.681 7。
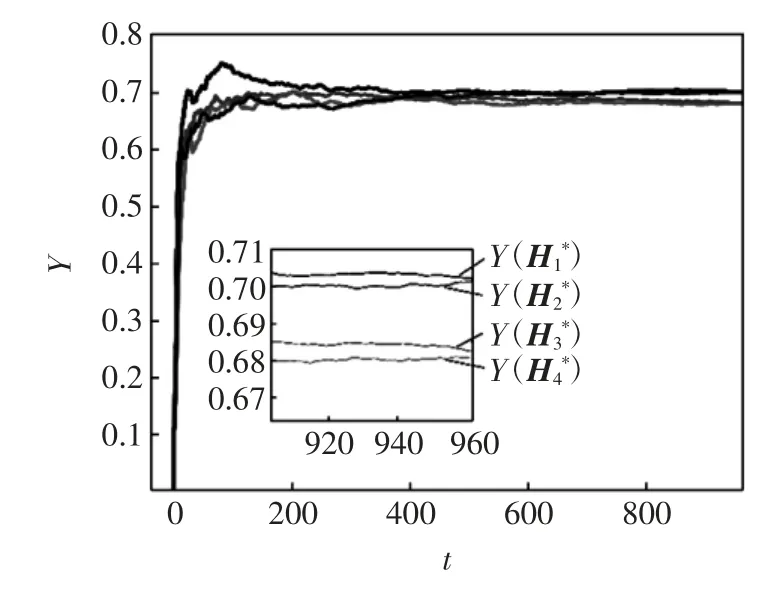
图2 Lévy 跳噪声对最优捕获策略的影响Fig.2 Effects of Lévy jump on MESY
5 结语
研究在Lévy 跳、白噪声和时滞的扰动下,两捕食者-单食饵的三种群模型的最优捕获问题。首先根据合理的假设和相关定理得出:①当Γ1>Γ2>Γ3>1时,物种在平均意义上可持续生存,且;②当假设2 成立时,式(1)是依分布稳定的;③种群的最优捕获努力量为最大持续产量为;④时滞对两捕食者和食饵的最优捕获策略没有影响,而种群的最优捕获努力量和最大持续产量会随着白噪声的增强而减少,随着Lévy 跳强度的减小而减少。
文中研究了在3 种不同的环境扰动下关于两个捕食者单食饵模型的最优捕获问题。关于种群模型的研究大多只考虑了一种或两种环境干扰因素,为了更加真实地反映大自然中的种群问题,应对同时在多种环境下具有连续时滞的种群模型的最优捕获问题进行更加深入的研究。

