分数阶非线性混沌系统的自适应滑模同步
王春彦,邸金红,毛北行
(郑州航空工业管理学院 a.智能工程学院;b.数学学院,河南 郑州 450015)
0 引言
分数阶混沌系统在滑模同步方面取得的研究成果甚为丰富[1-4]。文献[5]研究了分数阶混沌不确定系统的滑模同步,设计出了巧妙的滑模面。文献[6]基于适应有限时间反演模糊滑模方法,研究了非线性系统分数阶混沌系统的同步,但考虑的不是高阶系统。文献[7]基于输入受限滑模反馈同步,研究了分数阶混沌系统的同步。文献[8]进行了不确定分数阶混沌系统的滑模稳定性分析。文献[9]通过滑模技巧研究整数阶非线性混沌系统的控制器设计。文献[10]通过设计自适应控制规则获得了混沌系统取得同步的充分性条件,但研究的是三维系统。文献[11]研究了分数阶飞行姿态的多向滑模控制,但研究的不是高阶系统。分数阶高阶非线性混沌系统的同步引起了众多学者的关注。例如,文献[12]通过构造分数阶滑模控制器研究了非线性整数阶混沌不确定系统的同步。文献[13]通过设计滑模控制器,研究分数阶非线性混沌不确定系统的同步。由于高阶分数阶非线性混沌系统同步应用的广泛性和挑战性,在以上研究的基础上,本文研究了一类分数阶高维非线性混沌系统的自适应滑模同步。
1 主要结果
定义1卡普托(Caputo)分数阶导数[12-13]定义为:
本文则考虑高阶分数阶混沌系统[13],可以用分数阶微分方程描述为:
(1)
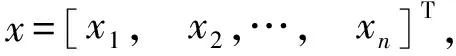
(2)
(3)
假设1设不确定项△g(y,t)和外部扰动d(t)有界,即存在未知参数m,n>0,使得:
|△g(y,t)| 假设2e1(0)=0,e2(0)=0,…,en-1(0)=0。 根据式(3)第n个方程,Dtqen-1(t)=en(t)→0⟹Dt(n-1)qe1(t)→0。 对上式两边使用拉普拉斯(Laplace)变换, s(n-1)qE1(s)-s(n-1)q-1e1(0)-s(n-1)q-2e2(0)-…-s(n-1)(q-1)en-1(0)→0, 其中:E1(s)=L(e1(t)),L为Laplace算子。根据Laplace终值定理有: 根据假设2⟹e1(t)→0,从而可得e2(t)→0,…,en-1(t)→0。 高阶整数阶混沌系统[13]可描述为如下方程: (4) (5) (6) 假设3e1(0)=0。 数值仿真以分数阶、整数阶混沌系统[15-16]为例: f(x1)=sin (ax1-bx1|x1|-(cx1)3),α=0.3,β=5.1,a=11,b=1.6,c=0.4,q=0.873时,出现混沌吸引子,以上述系统为主系统,设计从系统为: 定义ei=yi-xi,得系统: 混沌系统以多涡卷系统为例: f(x1)=sin (ax1-bx1|x1|-(cx1)3),α=0.3,β=5.1,a=11,b=1.6,c=0.4,以上述系统为主系统,设计从系统为: 定义ei=yi-xi,得系统 定理2中系统误差e1,e2,e3如图2所示。从图2中可以看出:3个误差变量在初始时刻距离原点较远,误差变量相差较大,随着时间的变化,3个误差逐渐趋于一致并向原点靠近,此时混沌系统的主从系统取得混沌同步。通过定理1和定理2的比较不难发现,定理2是定理1的结论推广和特例。分数阶系统的相关结果相对于整数阶系统表现出更优越的性能,主要是因为定理1设计的是分数阶滑模面,因而系统误差更容易被驱动到滑模面,收敛速率更快,需要更短的时间取得同步。这也体现出分数阶微分方程建模的优越性和系统特点。 图1 定理1系统误差 图2 定理2系统误差 研究了不确定分数阶非线性高阶混沌系统的自适应滑模同步,推导出一种滑模控制律、控制器及适应控制律。获得高阶不确定混沌系统自适应滑模同步的两个充分性条件,得到的结论说明高维不确定混沌系统满足适当的假设条件能够获得自适应滑膜同步,使用MATLAB软件数值仿真检验了结论的正确性。设计出收敛性更强的滑模函数是下一步考虑的问题。
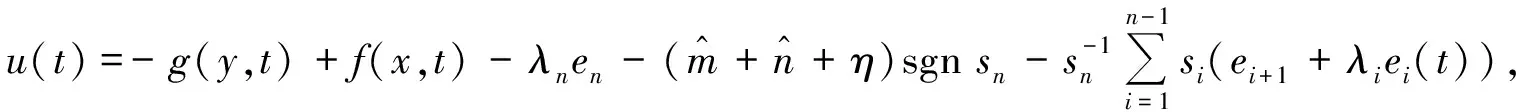


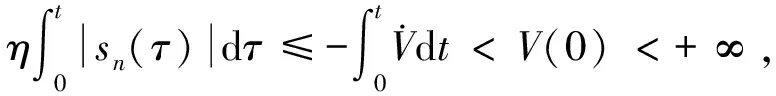
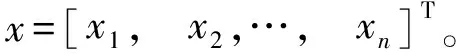
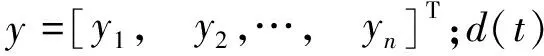

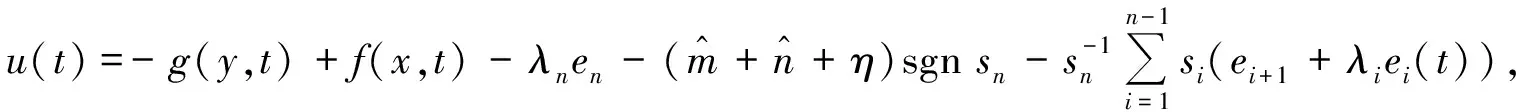



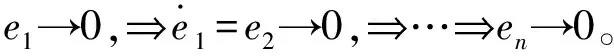
2 数值仿真





3 结论

