问题引导，层次递进

柏黎平

摘要：数学学习以发展学生数学学科核心素养为导向，而深度学习是实现发展学生核心素养的重要途径。以“平方根”第一课时为例，以层层递进的问题引导，探讨引发学生课堂深度学习的数学教学实践。

关键词：问题引导;数学课堂;深度学习

近日，笔者接到了一个公开课任务，内容是人教版七年级下册“平方根”第一课时。本节内容初看相当简单，就是平方根概念的引入与表示。“越简单的课越不好上！”这是所有初中数学教师的教学共识。如何在教材原有的基础上结合学生实际设计出一节较为理想的课，如何促进学生的深度学习是值得思考的。根据最新的数学课程标准要求：数学教学要以发展学生数学学科的核心素养为导向，创设合适的教学环境，启发学生思考，引导学生把握数学学习内容的本质。在数学课堂教学中，学生是教学活动的主人，因此，教师要放手让学生参与数学学习的各个环节，从而使学生真正成为课堂学习的主体，最大限度地引发学生探究知识的内驱力，引导学生主动在课堂中参与实现有深度的学习，促进学生实践能力和创新意识的发展。

结合本课内容的数学史演进历程和上述要求，我最后确定了在学生原有知识的基础上，通过层次递进的问题引导学生主动探索求知的课堂教学方式。下面就本课的教学过程谈谈自己的一些想法。

一、情境问题来源于生活

数学课堂，创设问题情境是非常重要的，情境引入设计应该简练而又有意义，应该具有导向性。按“问题教学法”设计的要求，设计问题不仅要认真分析学生在认知过程中的内在特征，从思维的规律出发，从培养学生具有良好的思维品质出发，而且要深刻分析教材本身的内在联系，从新旧知识中找到学生兴趣的激发点。本课的情境引入以“平方根”概念的产生为主要目的。教材的引入以实际问题“要剪面积为25的正方形纸片，表示该纸片的边长”为主，但我认为这在“非已知平方数”平方根的表示的引导上还有一定的欠缺。本课教学内容很容易让学生联想到“1的平方根会表示，那么2的平方根是多少”的问题，这恰好是本课的重点和难点。于是，我在本课引入时设计了两个递进的问题：

问题1：一个正方形的面积为1，它的边长是多少？

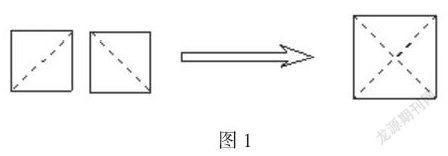
问题2：把这样的两个正方形经过适当的裁剪，你能拼成一个面积为2的正方形吗？如果可以，那么此时该正方形的边长是多少？

其中，第一个问题复习了新知识，并为应用新知识做好了准备;第二个问题具有一定的挑战性，学生刚开始可能认为不行，但动手操作探究之后，会发现是可以完成的（如图1所示）。

由上述探究问题产生了本课所要探究的重点问题：面积为2的正方形是存在的，但它的边长是多少呢？可以表示吗？用数学语言表述为：“若a2=2，a=？”这就引入了新课。同时，这个问题将会成为本课学生探究的一根主线，它将串联起全课的教学内容。

二、引发新旧知识冲突

教学中，由于教学内容的不同，会存在不同的内在关系，如新旧知识之间、已知与未知之间、因果之间的关系等。在这些关系中，我们要仔细分析，从中找出主要的关系，以激发学生探究问题的兴趣点。

在本课中，由情境引入我们可以发现现在的主要问题是：原有的旧知识已经不够我们解决问题了，需要新知识的介入。于是，我们就可以顺理成章地给出第三个问题：

问题3：可以发现的确存在一个数的平方等于2，如何来描述这个存在的数？

课堂上，教师可以让学生进行自主表述，在此基础上，再给出数学上的规范表述：“一般地，如果一个数的平方等于a，那么这个数叫作a的平方根。”同时，师生一起根据文字写出概念的代数表示法。接着，结合情境引入中第一个问题的结论解释平方根的意义和代数求法，并概括“关键是找到平方是1的数”，进行知识的迁移。然后，学生会想到（或教师引导学生）用所习得的新知识“平方根及其求法”去解决情境引入中的第二个问题。学生会发现：问题仍然无法解决，由于2不是学过的平方数，所以找不到平方是2的数。但是，学生也有一定的收获，他们结合刚刚学到的平方根概念，建立起了“a是2的平方根”的初步印象，知道目前要求2的平方根。

（一）深化概念内涵

雖然没有完全解决心中的疑惑，但不要紧，学习方面的点滴进步都很宝贵，我们继续探究。紧接着，教师引出了第四个问题。

问题4：求下列各数的平方根：

100，9，144，          ， 0，-4，-1

思考：通过研究上面几个数的平方根，你觉得有什么要总结的吗？

因为所给的数是熟悉的平方数，学生能较快得出答案，并且概括出：正数有两个平方根，它们互为相反数;0的平方根只有一个，就是0;负数没有平方根。

教师通过本题可以让学生对平方根的概念和求法等知识进行强化，同时又通过计算、观察、概括锻炼了学生观察问题和概括总结的数学能力。既然又收获了新知，教师和学生可再次回到情境引入环节中的问题2，看看这一次能否解决。此次，学生有更进一步的收获：正数2会有两个平方根，即a的值有两个，但就是无法表示出来。虽然仍旧无法解决问题，但又有所收获，这点收获也是支撑学生前进的动力。于是，学生又继续探究下去。

（二）固化研究成果

经过两次探究，学生获得了进步，但无法完全解决问题。此时，学生的胃口被吊得老高，应该是欲罢不能，探究问题最终答案的积极性更高了。于是，教师赶紧推出第五个问题：

问题5：从之前的数学学习中我们知道，每一个数学概念都有专用的表示方法，那么一个非负数的平方根是如何表示的呢？

此问题由教师直接教授。第二个概念性内容：一个正数a的正的平方根，叫作a的算术平方根，记作“      ”，读作“根号a”，另一个负的平方根是它的相反数，表示成“-       ”。教师及时总结：正数a的两个平方根记作“±       ”，而0的平方根是0，所以记作“     =0 ”;求一个非负数的平方根的运算叫作开平方，所以      中的a称为被开方数，显然a ≥0。此段教学内容新知识比较多，学生可能不会完全理解，教师可以再结合上面例1中的题目加以解释，通过举例明确求平方根的步骤和表示方法。

（三）例题探究2，对比感受概念表示方法

由于例1的数都为平方数，缺乏本课的重点“非已知平方数”的平方根的求法，我们需要进行适当的变式训练以突出本课的重点，也就是问题2所要解决的问题。于是，教师给出第六个问题。

问题6：将下列各数开平方：

（1）49              （2）1.69         （3）3

学生对（1）（2）题的解决不存在困难，解决第（3）题有所困难：已知3有两个平方根，但无法表示出来。这时，教师再给予明确的解释：“保留根号，‘±     。”至此，真相大白，学生马上会想到用最新的知识来回到本课引入时无法解决的问题，答案为“     ”。终于成功了，问题得以解决。接下来再进行适当的训练，让学生对本课所学新知识有一个强化和迁移的过程。

当然，学生可能又产生一个新的问题：“      ”到底是怎样的一个数呢？这就让我们留待下一节课去探究吧，我们又为下节课找到了探究问题的理由了。

以上就是笔者“问题引导、层次递进”的“平方根”第一课时的设计思路。本课以求“2的平方根”问题为一根主线，通过层层递进的几个数学问题，串起本课要学习的各个知识点，引导学生逐步进行探究，使学生的认知从模糊到清晰，引发学生深度思考，最终得出问题解决方案。这样的设计比较符合学生探究新知、认识新知的规律。

参考文献：

[1]王斌兴.在欢乐中成长：名师讲述最具活力的课堂愉快教学[M].重庆：西南师范大学出版社，2008.

（责任编辑：奚春皓）