指向深度学习的数学“问题链”设计

方伟 徐伟

摘要：探讨如何遵从“问题链”教学的动机性、关联性、思维性和多样性等特点，运用“知识联系”“数学活动” “题目变式”等策略进行“问题链”的设计与实施，开展有意义的深度学习，为学生深入进行数学思考提供机会，进一步提升学生的数学能力与思维品质，发展数学核心素养。

关键词：深度学习;“问题链”;数学思考

一、问题引发：无关联的问题群和压缩化的教学使学习普适性缺失

学生真实的学习历程是缓慢而复杂的。与之形成鲜明对比的，我们的课堂教学过程却是高速和极度压缩的，具体表现为以下五个方面。

（1）从目标上看，较少考虑学生的需求，没有深入分析学情，教师对知识打包压缩，教给学生。

（2）从内容上看，较少考虑学生的视角，且内容庞杂、信息量大，不进行区分、筛选、归纳，造成重复、低效学习，难以激发学生的学习兴趣。

（3）从进度上看，学生跟不上教学进度，教学进度与学生进度有落差，积压了难以完成的学习任务。

（4）从设计上看，较少从学生的学习角度进行“学习设计”，教师只从教学的角度进行“教学设计”。

（5）从方法上看，以教师讲授为主，学生没有自主思考和探究的过程，只是在被动地接受，学习无法深入，学生能力无法真正提升。

近年来，笔者积极探索尝试设计一系列问题，通过“环环相扣，步步推进”的“问题链”教学，引导学生探究知识本质，进入基于理解、迁移应用的深度学习状态，促进课堂教学向学生深度学习的方向转型。

二、变革方向：以问题链为脚手架的深度学习设计实践

（一）深度学习的理念

深度学习，就是在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。通俗地说，就是在已有的经验和认知体系下，通过对知识的深层次理解，建立起一种内在的、由此及彼的逻辑关联。深度学习基于学生自发和自主性的学习动机，依靠学生对问题本身探究的内在兴趣，是一种长期的、全身心投入的持久学习力。

（二）“问题链”的内涵

“问题链”通过独立又关联、具有系统性和层次性并层层推进的问题组驱动学生的数学思考，让学生在问题解决中实现数学再创造，在再创造过程中建构新知识、体验数学思想方法。从形式上看，“问题链”是环环相扣的。从目标上看，它步步深入，将疑问和目标通过“锁链”连在一起，通过一系列的设问，让学生的思维得到碰撞、产生共鸣。

（三）“问题链”的设计原则

1.动机性

“问题链”的设计要尽可能激发学生的兴趣和求知欲。教师要充分考虑学生的最近发展区，编排富有感性体验和趣味性的问题组，并创设真实的问题情境，营造积极的数学文化，将学生真正带入有意义的数学学习活动中来。

2.关联性

“问题链”的设计强调为学生提供数学思考的基本脉络，倡导让学生在思維脉络中产生问题、研究问题。数学知识和方法之间的关联成为数学“问题链”设计的逻辑起点。“问题链”设计的关联有效能够帮助学生建立起良好的认知结构，有助于学生实现知识与方法的迁移。教师要根据学生的学习现实与学习需求选择合适的关联在“问题链”设计中加以应用。

3.思维性

在教学中经常有这样的现象：教师问的问题过于直接，问题与问题之间跨度较小，限制了学生数学思考的空间。在“问题链”中，问题与问题之间的关联与跨度为学生进行多元思维与探索提供了可能。“问题链”中的各问题之间应该体现基本的思维方法，以便学生经历像数学家一样的思考过程，在思考过程中培养学生基本的数学思维，将学生的数学思考逐渐引向深入，从而使学生获得较高认知水平的数学能力。

4.多样性

由于数学内容类型的多样性及教育目标的丰富性，具有适切的内容特征及目标特征的“问题链”也是多样的。“问题链”设计要杜绝单一和僵化，多根据不同特点的教学内容，采用不同类型的“问题链”，促进学生对数学的深度学习。

三、实施路径：基于“问题链”的深度学习探究

（一）实施“问题链”教学的具体策略

1.“知识联系”策略——利用新旧知识之间的联系设计“问题链”

在教学过程中，若能将新旧概念间的联系点设计成“问题链”，通过对“问题链”的回答，引导学生建立起新旧知识间的联系，在新知识有生长的根基、旧知识有延伸的活力的基础上猜想并验证，就可以使学生比较容易地掌握新知识。

例如，在教学浙教版八年级下册的“正方形的定义”后，笔者设置了以下3个问题。

问题1：正方形有哪些性质？

问题2：哪些图形的性质正方形都具有？

问题3：正方形具有而一般矩形和菱形不具有的性质有哪些？

这3个问题，层层递进，让学生感受到新旧知识的变化和联系，将零散的、割裂的知识在头脑中建构起一条知识链，生长出纵横连通的“知识树”，构建起知识之间的深度联系，使数学知识结构化完善。

2.“数学活动”策略——利用数学活动设计“问题链”

通过动手操作、观察、猜想、分析而进行的数学活动，也指根据常识和已有经验，通过合情推理、假设与证明而进行思维实验。以数学实验为切入点设计的“问题链”，以完善学习者的经验结构为基础，在由直观感受上升为理性分析的过程中，提高学习效率。

3.“题目变式”策略——利用题目变式设计“问题链”

通过改变问题的条件、结论或转换问题的形式或内容来设计“‘问题链变式”。如果问题难度比较大，让学生无法承受，就必须插入问题组形成“问题链”，以减少问题和问题之间的思维跨度，形成“‘问题链变式”。

（二）基于“问题链”的深度学习教学案例设计

现以浙教版七年级上册“3.2实数”为例，阐述笔者基于“问题链”的深度学习设计理念。

1.教学联结点

在实数的内容教学之前，学生对有理数的概念和运算已有了深刻的理解和掌握，根据数的扩充一致性，类比有理数概念（如相反数、绝对值）和运算（法则、性质、运算律）来进行实数的学习，以此给出实数的概念与分类。

2.“问题链”的设计

开场白：科学家对数的研究，经历了漫长的历程。自然数帮我们解决了计数的问题。进入初中阶段，我们引入正负数和数轴的概念，得到了新的整数和有理数概念。

问题1：现在我们对整数可以怎么分类？

问题2：我们如何表示分数？

问题3：有理数如何进行数学表示？

通过这3个问题，让学生回顾已有知识，感受从自然数到整数再到有理数的扩充过程，感受数的扩充是因为数学自身发展的需要，系统建构、复习有理数的有关知识。

问题4：有理数都可以表示成  （p、q为整数，p、q互质，且p不为0）的形式吗？有没有特殊形式？

问题5：学校美术创意比赛要求作品的尺寸不能大于30平方分米 ，小明的参赛作品是一块边长为5.4分米的正方形画布。

小明的作品大小符合要求吗？这个问题的实质是什么？运用了哪种运算？

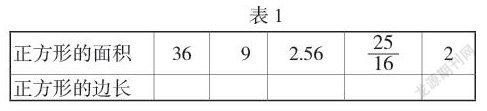
穿插活动，填写下表（如表1所示）。

问题6：如果知道正方形的面积，我们能够求得正方形的边长吗？如果正方形的面积为2，边长是多少？

明确问题的实质是“已知一个正数，求其平方根”，是乘方的逆运算，为接下来的学习做铺垫。4个问题组成的“问题链”，引发学生对现有有理数不足以解决面积问题产生思考，让学生强烈感受到有理数的局限性，认识到还存在我们不了解、不知道的一类数。

3.基于“问题链”的深度学习案例反思

（1）追求概念性理解。对“面积为2的正方形的边长到底有多大”这个问题展开研究，感知这样不是整数、也不是分数的“非有理数”的存在;用无限逼近法进行估算，感知不是有理数，让学生真正理解无理数。

（2）指向知识结构化。实数教学基于学生已有知识的最近发展区，从已学的整数和有理数着手，梳理已学知识，为后续类比进行铺垫，融入以往经验，让教学得以提升并形成结构。

（3）发展高阶思维。为了让学生探讨 到底有多大，笔者设计了二分法的估算，此举既为探索数学规律活动，也为培养学生洞察事物本质的能力。学生经历了对数据的理解和算法的合理选择，以及对结果的正确判断，提高了逻辑推理能力，优化了自己的高阶思维品质。

四、学习深化：有品质的“问题链”设计促进深度学习

在基于“问题链”的深度教学中，笔者力求“弹性设计与动态生成”“学生能力和素养培养”的和谐统一，一年来积累了一些经验，学生学习高效了、思维有了深度。

（一）深度課堂——重探究，重思维

“问题链”教学促进学生对数学的深度理解，并实现深度学习目标。“问题链”教学有利于学生开展探究性学习活动，驱动学生的思考，给学生提供深入思考与探索的空间，唤醒学生的思维意识，引领学生进入高阶思维。

（二）改变学力——善发现，善提问

“问题链”构建了教师“教”和学生“学”之间的纽带。学生通过发现问题、猜想探究、验证说明、再提出新的问题，不断地发现问题、提出问题、解决问题，主动探究新知，自主学习能力不断得到提升。

（三）提升素养——会整理，会反思

“问题链”数学课堂教学尝试是整合性学习的一种回归，学生会梳理知识的内在联系与本质，反思如何用联想、结构的方式去学习，丰富和完善原有的认知结构。

基于“问题链”的深度学习，转变了教师的教学观念，让学生的学习真实地发生，将课堂学习推向更深层次的理解性学习。

参考文献：

[1]刘月霞，郭华. 深度学习：走向核心素养（理论普及读本）[M].北京：教学科学出版社，2018.

[2]唐永.指向深度学习的数学课堂“追问”设计[J].教学月刊，2020（11）.

[3]徐晓燕.概念性理解与数学概念教学：基于数学任务设计的视角[M].上海：上海教育出版社，2020.

（责任编辑：奚春皓）