基于Matlab的电动机模态测试系统

王玉彬， 孙鑫晖， 李祥林， 马文忠

（中国石油大学（华东）新能源学院，山东青岛266580）

0 引 言

评价一台所设计电动机性能的优劣，既要考虑其感应电动势的正弦度、功率／转矩密度和效率等基本电磁性能指标［1-5］，又要衡量电动机运行时产生的电磁噪声对周围环境造成的影响［6-7］。因此，使得学生难以系统、全面地掌握高效能电动机的设计、分析方法与电动机性能评估的有效手段。

现有教学实验条件大都可以满足电动机的基本电磁性能实验测试，而电磁噪声的实验测试则较难实现。这主要是因为电动机噪声由电磁、空气动力和机械噪声三部分组成［8-10］，而将电磁噪声直接分离出来具有一定难度。现代计算机技术的迅速发展与商业化有限元分析软件的广泛应用，为电磁噪声的准确预测提供了新思路。具体为：首先采用模态测试系统得到电动机定子的结构模态测试数据；然后基于该模态数据，采用ANSYS软件得到电动机定子的泊松比、弹性模量等结构参数，从而确定采用有限元软件进行电磁噪声分析时电动机定子的精确模态；最后将电动机定子所承受的径向电磁力与定子的精确模态相耦合，采用有限元软件进行电动机的振动及电磁噪声预测分析。

可见，采用模态测试系统得到电动机定子的结构模态测试数据是对电动机进行电磁噪声预测分析的关键环节。然而，目前主流的模态测试系统，如比利时LMS 公司的TEST.LAB、丹麦BK 公司的PULSE、Crystal Instruments 公司的EDM Modal 以及奥地利DEWESoft公司的SIRIUS测试系统，价格昂贵，不适于多组别的学生分组实验。因此，本文基于具有开放接口的NI公司USB4431 动态分析仪开发了一套电动机模态测试系统［11-12］，从而测试获得电动机定子的模态数据，以期准确预测电动机的电磁噪声。

1 系统构成

电动机模态测试平台主要包括CT1050C 冲击力锤、加速度传感器、USB4431 动态分析仪、基于Matlab的模态测试软件以及电动机悬挂支架等［13-15］，其连接结构示意图如图1 所示。模态测试时，首先采用无阻尼弹力绳把电动机定子悬挂至半空，保持低阻尼接近零阻尼的状态，由冲击力锤对电动机定子施加激励，加速度传感器采集定子响应信号传递至动态分析仪，最后由上位机中的Matlab 模态分析程序计算得出实验对象的频响函数曲线、固有频率、模态振型。图2 所示为系统的实物图。

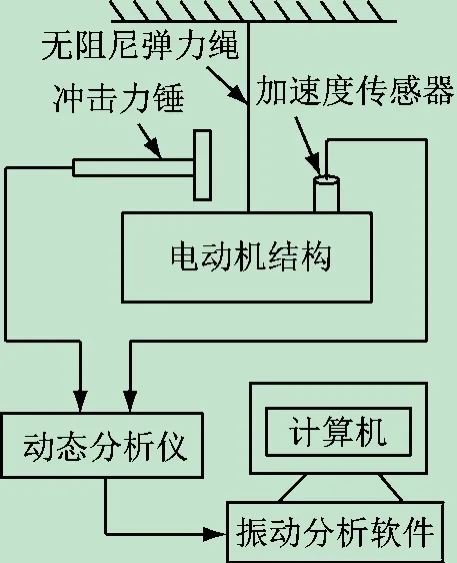
图1 模态测试系统构成示意图

图2 模态测试系统实物

2 测试流程

本文的模态试验采用单参考点锤击测试法。以固定不动的单向加速度传感器作为模态参考点，力锤移动遍历所有的测试点，得到频响函数矩阵完整的一行。需要说明，锤击法实验时需要在上位机模态分析程序中进行预触发设置，以保证力脉冲的完整性，避免力脉冲不完整导致的力谱失真。力锤激励后得到的完整力谱如图3 所示。力谱是一个衰减的频域函数，通常以衰减在20 dB内的频率为有效带宽。由于不同硬度的锤头有效带宽不同，当敲击力度相同时，锤头的材质越硬，锤击产生的带宽越宽，所以应根据具体的实验要求更换不同材质的锤头。

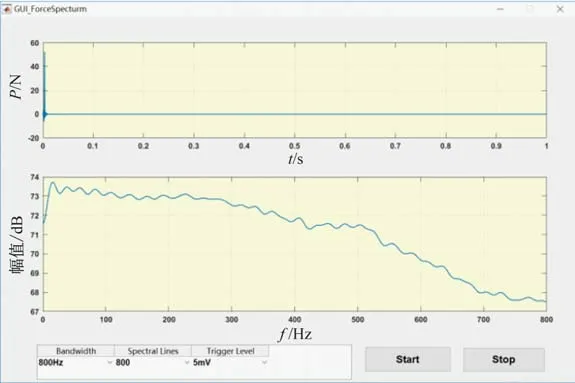
图3 力锤激励力谱

2.1 建立模型

首先在模态分析软件中建立所测试电动机的定子模型，模型网格按比例均匀划分并与力锤敲击点相匹配，如图4 所示。然后添加加速度传感器响应点和冲击力锤敲击点，并确定传感器位置角及敲击点位置角。由于实验目的是测试电动机外定子径向模态，所以传感器布置点和力锤敲击点要与外定子表面垂直，这样测得的振动数据方向才与实际振动方向相符合，以保证实验结果的精度。

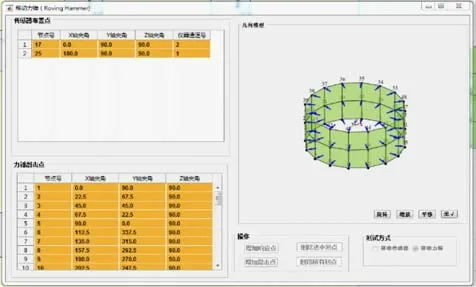
图4 定子模型

2.2 参数设置

建模完成后需设置实验所需的冲击力锤通道及加速度传感器通道，进行通道参数设置，如图5 所示。若需添加多个加速度传感器时，则根据传感器铭牌参数进行设置，当传感器及力锤采用数仅为1 时可将传感器灵敏度设为1。

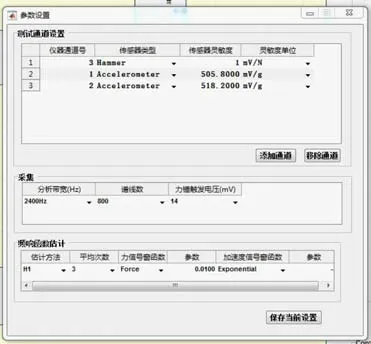
图5 通道参数设置

2.3 模态测试

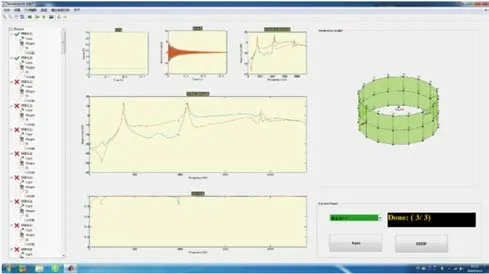
图6 模态测试软件界面

基于Matlab 的模态测试软件界面如图6 所示，该模态测试软件可以得到力锤激励的时域信号、频域衰减信号、频率响应函数以及相干函数。其中，频率响应函数（Frequency Response Function，FRF）是结构输出和输入激励之比。将测量得到的时域数据通过快速傅里叶变换从时域变换到频域，频响函数最终呈现于复数形式，可以表达为

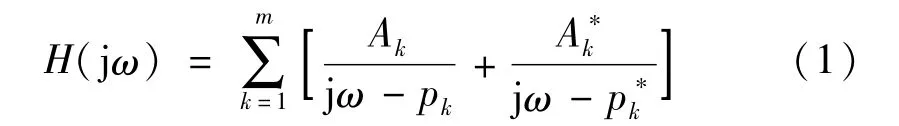
式中，分子中包含留数，而留数与模态振型直接相关；分母中包含了系统极点信息，也就是系统频率和阻尼信息。因此，从系统频响函数可以得到系统的全部模态信息。频响函数矩阵中单个元素可以表达为

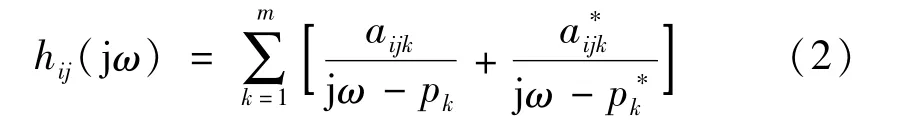
式中：hij为j点施加单位激励时，i点的输出响应。

力锤的激励函数要保证是脉冲函数，一旦出现了非脉冲函数即连击情况，会导致振动信号的采集失真。相干函数反映了多分量组成的输出信号中最大能量与输出信号的总能量的比值，体现了频响函数的测量质量。当所有测试点测试完成后，可以得到如图7 所示的频响函数曲线。将测试所得的频响函数矩阵进行奇异值分解，得到图8 所示的复模态指示函数曲线，该曲线明确地指示出测量频率范围内的各阶模态。

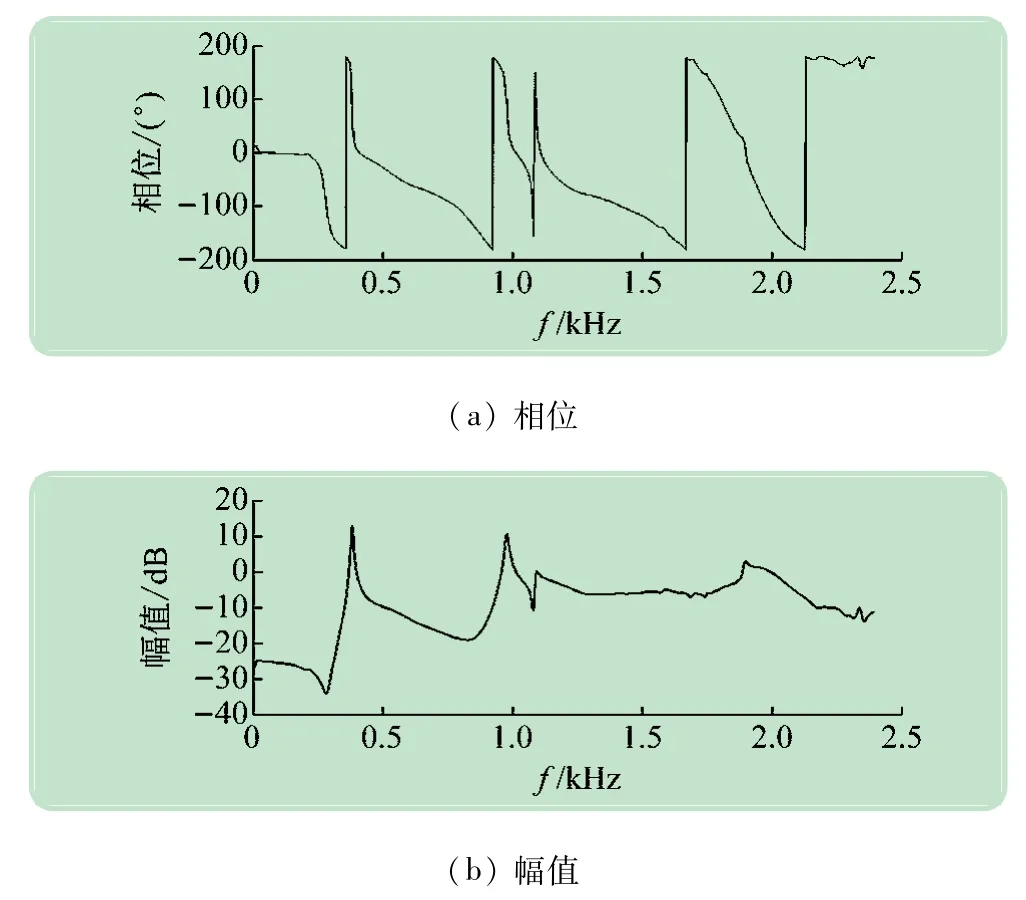
图7 频响函数曲线

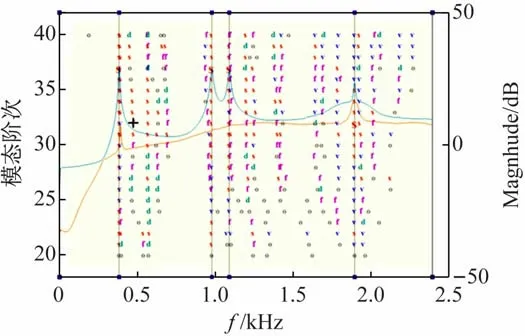
图8 复模态指示函数曲线

为验证所得测试结果的准确性，经实验测试可以得到模态置信度（Modal Assurance Criterion，MAC）如图9 所示。MAC是振型向量之间的点积，用于评价两个模态振型向量几何上的相关性，其计算得到的标量值介于0 ～1 之间。若MAC 接近于0，说明两个振型向量之间的相关性很小或者是正交的；如果MAC值接近于1，说明两个振型向量彼此平行或者非常相似。由图9 可见，实验所得不同阶次的模态基本正交，表明所开发的模态测试系统具有较高的可靠性。

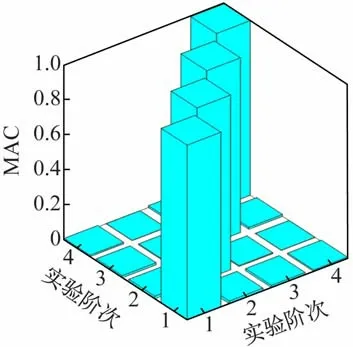
图9 模态置信度

3 电动机模态有限元分析

测试电动机定子的主要尺寸参数如下：定子槽数42，定子外径145 mm，定子内径95.6 mm，电枢长度60 mm。对图8 所示的复模态指示函数曲线进行参数识别，可以得到电动机定子的各阶模态振型及频率。在测试所得到的模态数据的基础上，采用ANSYS软件可以得到电动机定子材料的密度为8.0 g·cm3，弹性模量为190 GPa，剪切模量为75.4 GPa，泊松比为0.26。表1 给出了测试所得模态振型与有限元计算所得电动机各阶模态对比。由表可见，对电动机定子前三阶模态振型的固有频率而言，有限元计算结果与实验结果误差较小。其前三阶固有频率的误差分别为2.8%、3.7%、1.0%，这表明，基于实验所得电动机定子模态数据建立的定子有限元结构模型是可靠的，可以用来较为准确地预测电动机的振动及电磁噪声。

表1 定子模态及频率

4 结 语

本文基于Matlab 软件，针对电动机设计课程教学过程中存在的电磁噪声难以准确预测这一问题，设计开发了一套价格适中的电动机模态测试系统，用以测试电动机定子的结构模态数据，从而实现电动机电磁噪声的准确预测。该模态测试系统不仅适合多组别的学生分组实验，达到较广的受益面，而且能够准确、高效地测试电动机的模态和固有频率，有利于学生深入理解电动机设计的理论知识，较为全面地掌握电动机的设计、分析方法与电动机性能评估手段，培养学生的探索创新能力。同时，该系统也可以用于科学研究，具有一定的应用价值。