“化工装备密封技术”课程教学软件开发与应用

孙鑫晖， 郝木明， 左海强， 王增丽

（中国石油大学（华东）新能源学院，山东青岛266580）

0 引 言

“化工装备密封技术”是过程装备与控制工程本科专业的一门专业课［1-2］，该课程综合性较强。在课程的教学过程中，密封流体力学基本方程中的雷诺方程与非接触机械密封原理以及性能影响因素不易讲，不易学。原因主要有以下两点：①在雷诺方程的讲解中，侧重于介绍如何通过简化纳维-斯托克斯方程（Navier-Stokes equations，N-S）方程获得雷诺方程，通过公式推导的方式传授给学生，学生在学习过程中难以获得直观体验，削弱了学习兴趣，对如何进行工程应用更加不易掌握。②在非接触机械密封讲解中，其工作原理恰好需使用到雷诺方程，但对于复杂槽型的密封端面，无法直接通过解析法获得密封端面的压力场分布。如果采用自己编程或者商用软件（如FLUENT）对端面压力场进行数值求解，难度较高，超出课程的要求。

基于以上原因，为在有限的课堂学时中能获得更好的教学效果，在Matlab环境下开发一个非接触机械密封教学软件，将雷诺方程的求解与非接触机械密封的性能分析结合起来，为丰富课堂中教学手段、提高教学效果提供了一种新工具。

1 密封端面压力场的求解

1.1 控制方程

黏性流体在密封端面之间流动，通过动压效应产生开启力使得端面分开实现非接触运转。为简化数值计算，对分析黏性流体流动的主要控制方程N-S 方程进行简化［2］可以得到雷诺方程。通过对雷诺方程进行数值求解可以获得端面的压力场以及其他性能参数。

极坐标下雷诺方程的表达式为［3-7］：

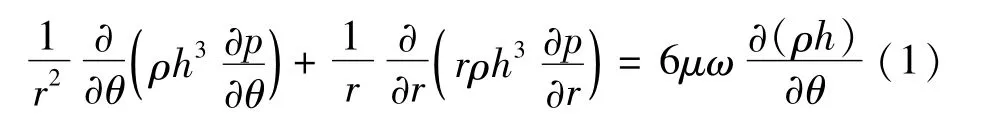
式中：h为密封面间流体的厚度，m；p 为密封面间流体的压力，Pa；μ为密封面间流体的动力黏度，Pa·s；ρ为密封面间流体密度，kg／m3；ω为轴的旋转速度，即动环的角速度，rad／s；r，θ 分别为极坐标系下的极半径和极角。

如果密封端面间流ρ 体密度为常数（例如液膜密封），则式（1）可写为：

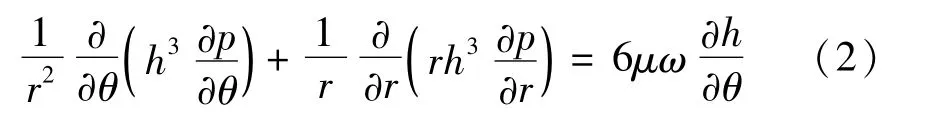
1.2 边界条件

在求解雷诺方程时需要用到边界条件，针对非接触机械密封，方程的边界条件有以下两类：

（1）强制性边界条件。静环内径处r ＝ri，p ＝pi；静环外径处r ＝ro，p ＝po。

（2）周期性边界条件

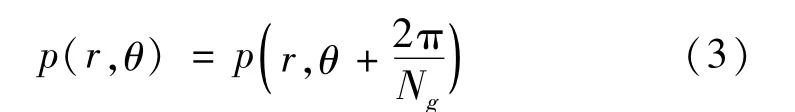
式中，Ng为密封端面中开槽数目。

1.3 控制方程的求解

本文采用有限差分法对雷诺方程进行离散［4］。图1 为有限差分法的控制体积图，为极坐标下节点和控制体积的标注方式。由于采用了周期性模型，只需要计算一个周期即可。

极坐标下雷诺方程式的有限差分表达式为［3-4］：

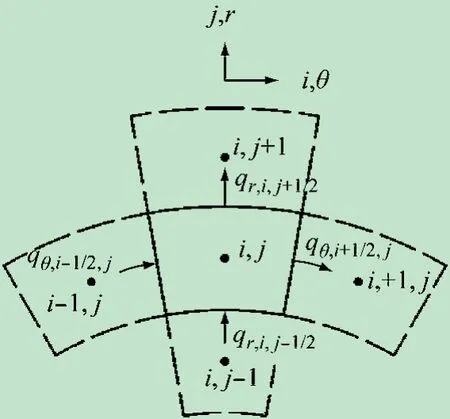
图1 有限差分控制体积图

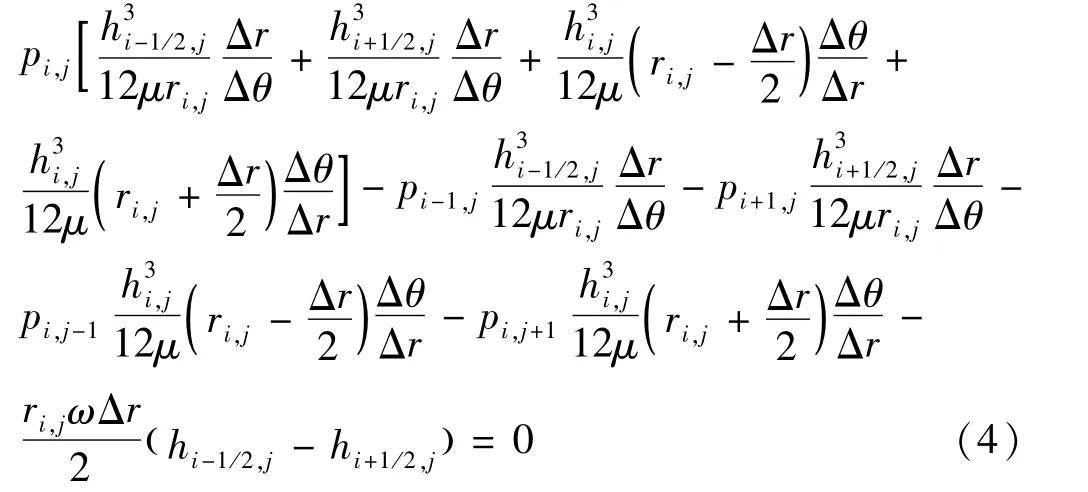
将式（4）改写为

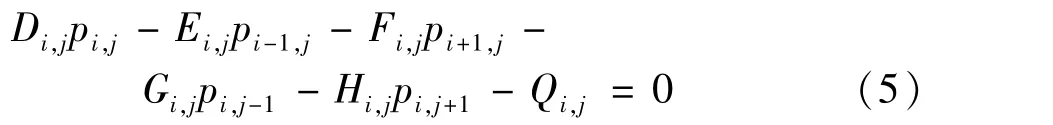
式中，Di，j、Ei，j、Fi，j、Gi，j、Hi，j、Qi，j均为系数。

采用逐次超松弛迭代（SOR）方法求解端面压力分布，迭代公式如下［3］：

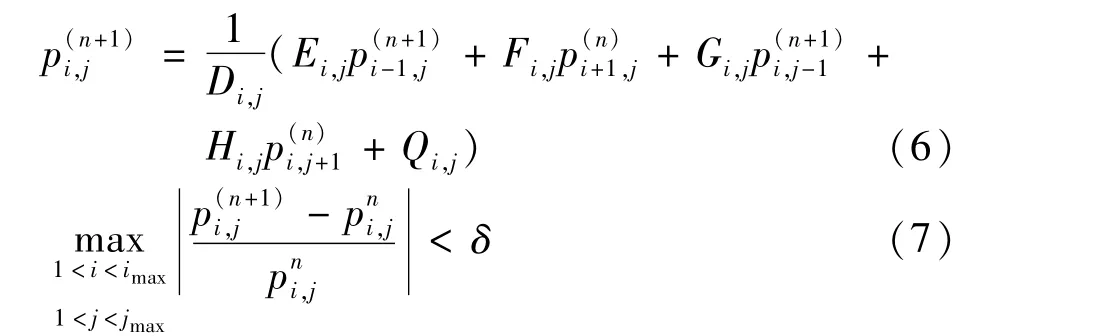
式（7）为迭代过程的结束条件［3］，通过最终的pi，j结果得到密封端面膜压。

以上计算是在给定流体膜厚度下完成的，如果指定了闭合力，则需要通过迭代寻找相对应的膜厚h，图2 所示为其迭代流程。

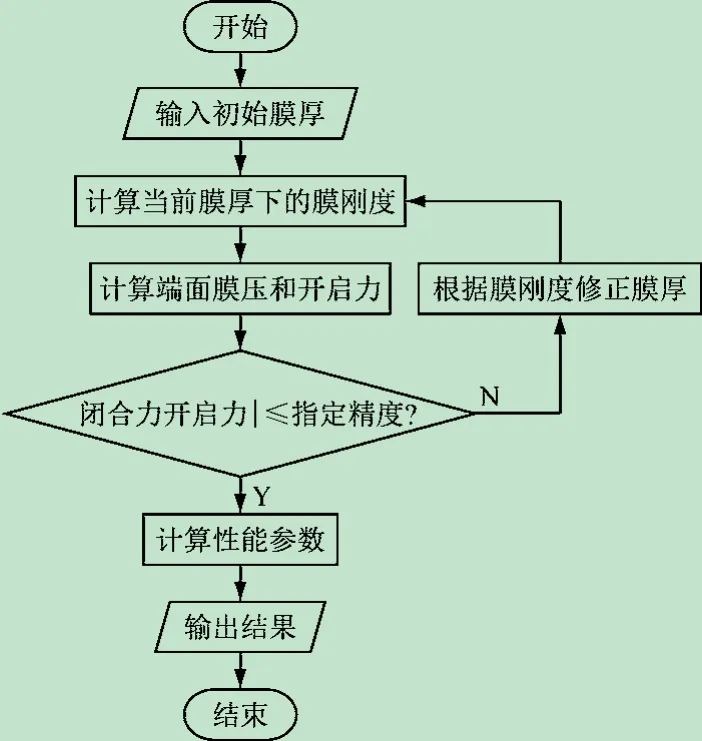
图2 定闭合力条件下计算流程图

1.4 稳态特性参数

当求解得到端面压力场之后，在此基础上可以获得稳态特性包括开启力、液膜刚度、泄漏量及摩擦系数［4］。

（1）开启力。将所计算的液膜压力分布沿整个计算区域积分，再乘以密封槽个数Ng可得开启力，方向垂直于密封端面：

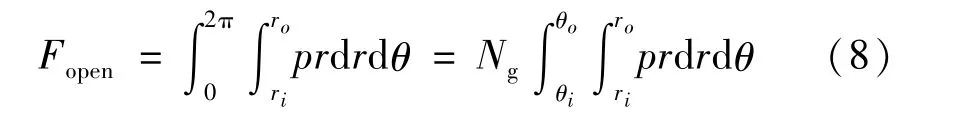
（2）流体膜刚度系数。设密封处于稳态平衡位置时液膜厚度为h0，轴向微扰Δh 产生的液膜开启力增量为ΔFz，则定义液膜刚度为：

（3）端面摩擦力。由于径向流动相对于周向剪切流很小，因此在计算密封端面摩擦力时可忽略不计，则端面摩擦力为

式中：

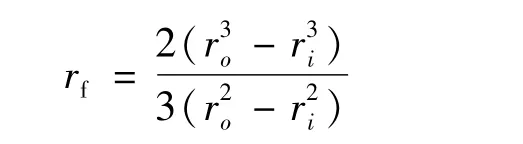
为当量摩擦半径；

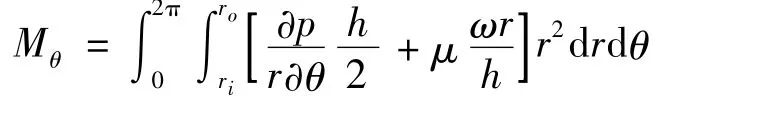
为摩擦扭矩。

（4）泄漏率。密封的泄漏率采用下式进行计算：

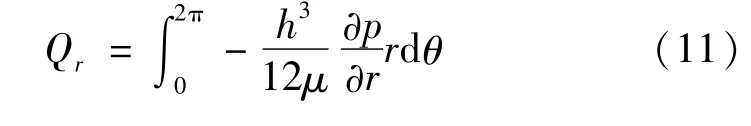
2 教学软件的设计

2.1 整体设计思路

非接触机械密封教学软件主要包含3 类槽型的性能分析，分别为对数螺旋槽、人字槽和枞树槽。对于每类槽型都能够进行不同结构参数、操作参数下的性能分析。在软件中通过树型控件选择不同槽型，软件的操作界面如图3 所示。

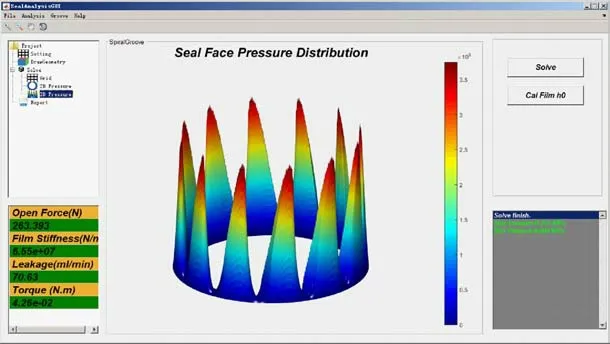
图3 软件的操作界面

软件开发环境为Matlab［9-15］，采用面向对象的设计方法［9］。根据机械密封的特点，将不同槽型密封共有的结构参数、操作参数、物性参数以及共有的方法封装到基类SealBase 中，然后将各类槽型密封定义为派生类，根据自身结构特点添加相应的成员变量与成员函数。软件中派生类包含了SpiralGroove、HerringboneGroove、FirTreeGroove，分类对应于螺旋槽密封、人字槽密封和枞树槽密封，图4 为UML类图，软件的总体框架如图5 所示。

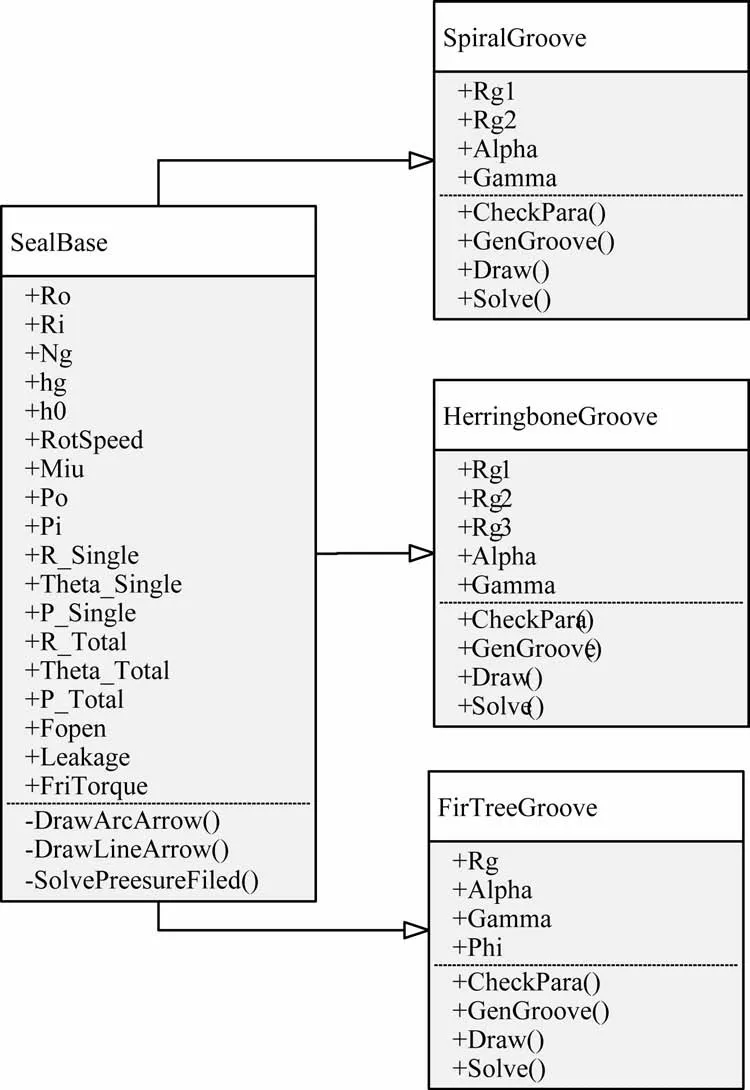
图4 不同槽型密封UML类图

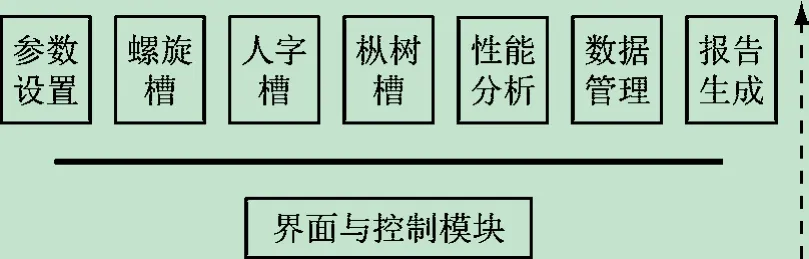
图5 软件的总体框架

2.2 软件的主要功能

软件能够对螺旋槽、人字槽和枞树槽非接触机械密封进行分析与演示。3 种类型密封槽型的几何结构如图6 所示。

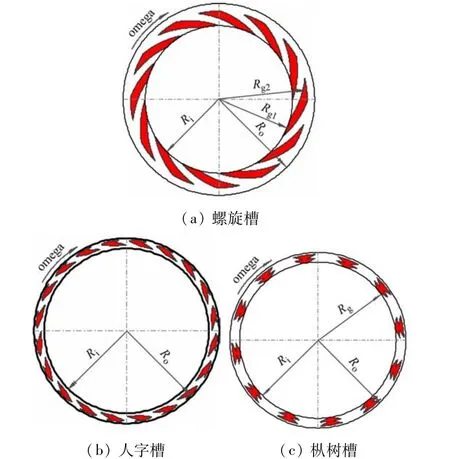
图6 软件包含的槽型

对于每种槽型的几何参数、操作参数和物性参数可以通过图7 界面进行参数设置。

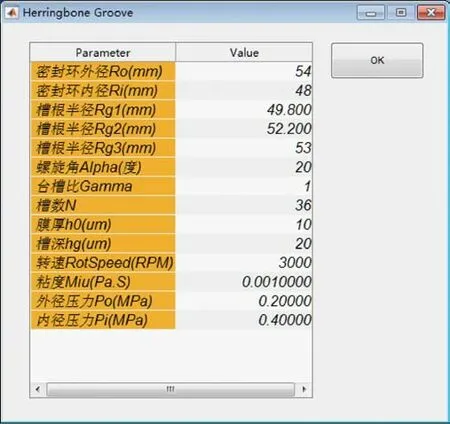
图7 参数设置界面

针对某种槽型，在使用1.3 中算法进行分析之前，需要判断某个计算节点是否在槽区内，进而确定膜厚。以螺旋槽为例，说明其判断方法。螺旋线方程为

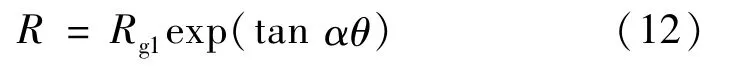
式中：α为螺旋角；Rg1、Rg2分别为槽底和槽根半径。一个周期内槽区所占的角度为

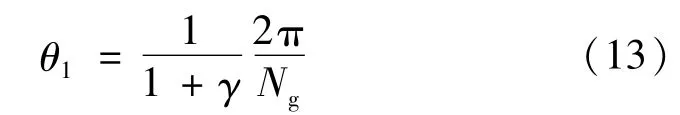
式中，γ为台槽比。

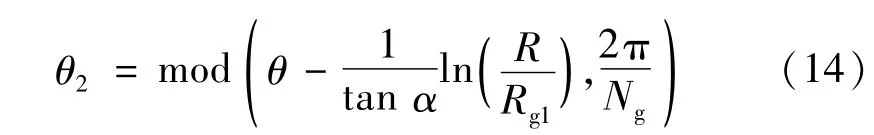
计算区域内任意的一点（R，θ）如果满足0≤θ2≤θ1且Rg1≤R≤Rg2，则该点落入槽区。图8 所示为一个周期内的网格划分以及槽区。

图8 计算周期内网格划分

所有参数设置完成后，可以计算得到一个周期的压力场数据，按照槽数将单周期数据组合到一起，得到完整的密封端面计算结果如图9 所示。

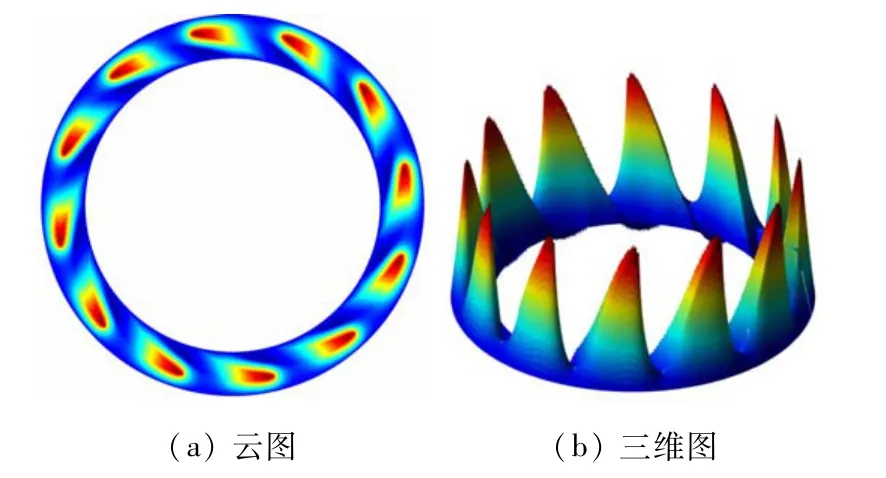
图9 端面压力计算结果

为帮助学生更好地理解各种参数对密封性能的影响，可设置某个几何参数、操作参数、物性参数的变化范围，软件就可以给出在此范围内性能的变化规律，如图10、11 所示。表1 所示为密封参数。

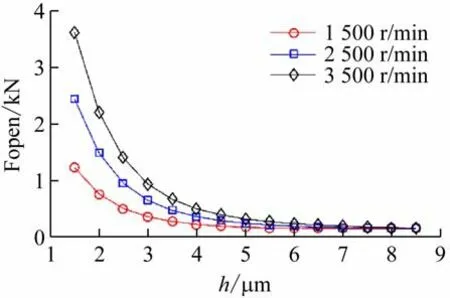
图10 膜厚对开启力影响

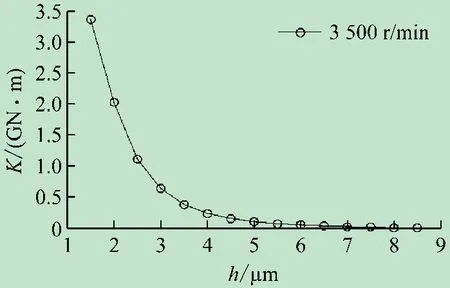
图11 膜厚对膜刚度的影响

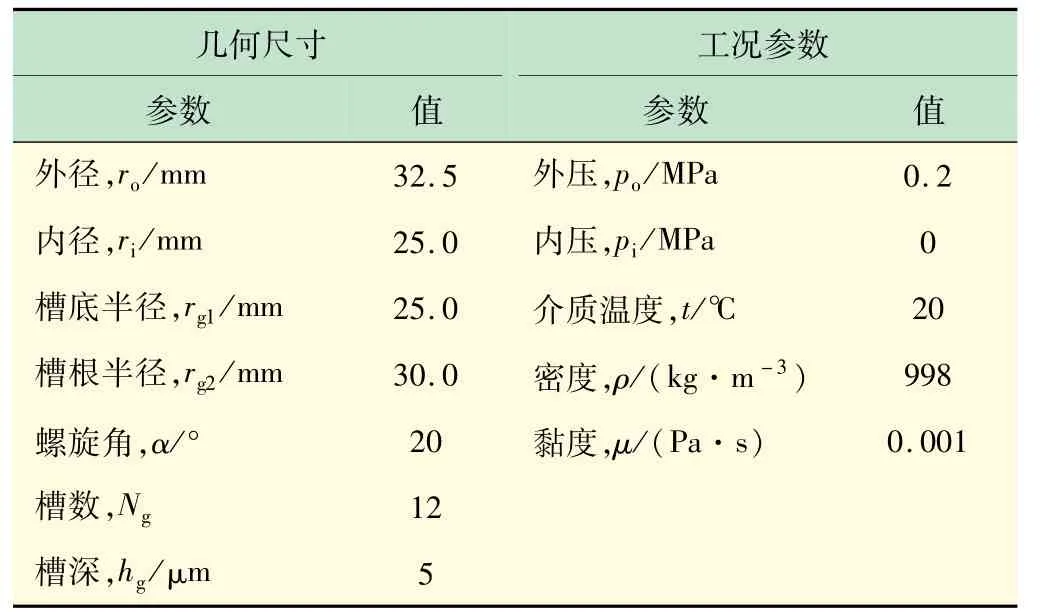
表1 密封端面几何尺寸及工况参数

为让学生对计算结果有更加直观的感受，在软件中添加了动画演示功能，使得参数变化对性能的影响更加清楚。软件能将动画保存为AVI 或者GIF 格式，方便教学素材的制作，界面如图12 所示。

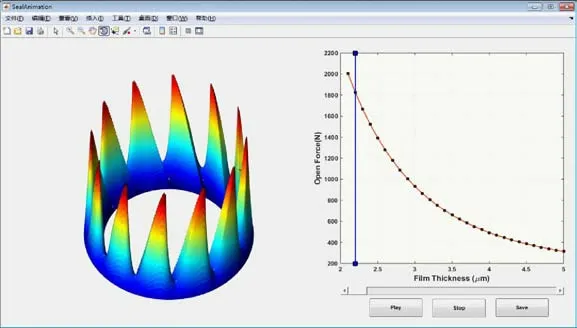
图12 动画显示界面

2.3 软件在教学应用中主要优点

本文建立的教学软件为学生提供了一个直观认知非接触机械密封的有效窗口，改善了传统的推导公式型教学方法。任课教师在课堂教学过程中可以通过引导学生在计算机上实际操作加深对密封流体力学与机械密封原理的理解，并直观体会到关键参数对密封性能的影响。

（1）软件具有较好的可视化效果。教学软件最显著的优点就是具备良好的可视化效果。通过曲线、云图、三维图、动画等方式清晰直观地展现给学生，有利于强化学生对该方面知识的理解，为后续内容的学习打好基础。

（2）软件的扩展性能。在软件编写的过程中，采用面向对象的设计方法，在后续内容扩展上更加方便。同时源程序采用类进行封装，易于实现且开源，学有余力的学生可以通过自行编程，对密封问题进行自主模拟。有助于进一步提升学生的计算机编程水平。

3 结 语

通过求解雷诺方程对非接触机械密封教学中的案例进行了数值模拟，在Matlab 环境下开发了非接触机械密封教学软件，该软件包含了教学中常见槽型的分析模块。学生既可以通过软件直观的获得分析结果，也可以在此基础上进行二次开发。相对于传统课堂与实验教学方法，本教学软件可视化效果较好，便于交流，值得在“化工装备密封技术”教学中进行推广。