基于流场-电场耦合的含水合物模拟岩心电学特性数值实验

邢兰昌， 齐淑英， 李 馨， 魏 伟， 韩维峰

（1.中国石油大学（华东）控制科学与工程学院，山东青岛266580；2.中国石油勘探开发研究院新能源研究所，河北廊坊065007）

0 引 言

天然气水合物（简称水合物）是水与天然气（主要成分为甲烷）在高压低温条件下形成的类冰状结晶物质［1］。自然界中水合物广泛分布于内陆湖的深水环境与冻土带和海底0.1 ～1.0 km以下的大陆斜坡和深海盆地的沉积物［2-4］，其在沉积物中以多种分布形式存在，宏观上有分散型、块状、脉状等；微观上有悬浮、接触、胶结等，多种空间分布形式导致含水合物沉积物等物理性质呈现各向异性［5-6］，从而为刻画含水合物沉积物的性质以及评价含水合物饱和度带来了困难。

为了深入研究含水合物沉积物的电学特性以及电学参数与含水合物饱和度之间的关系，研究者对野外钻探获取的岩心或者人工合成的样品进行测试。但是，由于水合物通常赋存于固结程度较弱的沉积物中，而且水合物稳定性对温度压力条件的依赖性高，所以野外钻探取样技术非常复杂、取样难度大且成本高。实验室内制备人工样品并进行测试是一种有效的研究手段。在实验过程中已逐步采用多种监测技术以尽可能直观地获取水合物的空间分布特征［7-10］，如CT、ECT等。但是CT技术要求样品小，ERT 技术分辨率受到限制。此外，开展水合物模拟实验测试耗时较长、可模拟的实验条件有限、探测信息较少（如无法获知物理场参数的空间分布信息），岩石物理数值模拟为克服上述困难提供了一条可行的途径。

本文基于流场-电场耦合的有限元数值计算方法研究含水合物模拟岩心的电学响应特性。通过流场计算获得多孔介质中油／水空间分布来模拟水合物／水在岩心中的微观分布，通过电场计算获得含水合物／水模拟岩心的电学特性，最终形成一套针对含水合物模拟岩心开展岩电数值模拟实验的方法。

1 岩电数值模拟实验

首先需要获得具有不同含水饱和度的模拟岩心样品，然后对岩心样品进行测试获得电学特性参数。在实际岩心中建立不同含水饱和度的常用方法有油／气驱法、离心法、烘／风干法、半渗透隔板法和自吸增水法等［11-14］。

本研究数值模拟实验中采用驱替法来获得具有不同含水饱和度的模拟岩心。考虑到油与水合物电学性质和微观分布状态的相似性，利用水驱油过程所形成的油／水分布来模拟水合物／水在模拟岩心孔隙中的微观分布状态。基于COMSOL Multiphysics 平台建立含油水模拟岩心的流场-电场耦合数值仿真模型。

图1 所示为带有平板电极和环形电极的模拟岩心。首先将模拟岩心进行油饱和，然后固定出口压力，以恒定的流速从入口处注入水，对模拟岩心中的油进行驱替。通过调节模拟岩心和流体的性质以及驱替时间来控制油水两相在孔隙空间中的分布状态和含油／水饱和度；在驱替过程中采用上述两种类型的电极对处于不同状态的模拟岩心进行电学参数测量，进而分析电学参数与含油饱和度之间的关系。

图1 两端带有平板和环形电极的模拟岩心

2 耦合数值模型的建立

2.1 几何结构

建立如图2 所示的长18 mm、宽9 mm的二维多孔介质模型来模拟柱塞状岩心，其中骨架颗粒在多孔介质内以等径圆形交叉排列，圆的直径设定为1 mm。模型入口位于x ＝0 mm处，出口位于x ＝18 mm处。

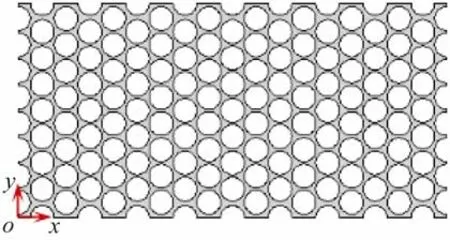
图2 二维多孔介质模型

2.2 边界条件和材料物性参数

采用COMSOL中CFD 模块模拟多孔介质孔隙中水驱替油的两相流动过程。数值模型采用速度入口和压力出口，在入口处设置注入水流速，在出口处设置压力值。初始状态时，多孔介质模型处于油饱和状态，驱替时在入口处注入不同流速（如7.81、31.24 mm／s等）的水来驱替多孔介质内的油。模型中设定水和油的典型物性参数为：水密度ρwater＝998.2 kg／m3、水黏度μwater＝1 mPa·s，油密度ρoil＝880 kg／m3，油黏度μoil＝0.02 Pa·s。

采用COMSOL中的AC／DC模块计算多孔介质区域的电场参数。模型中的电极材料为铜，将油视为不导电的物质，其电导率设置为0 S／m，相对介电常数设置为2.2，水的电导率设置为0.05 S／m，相对介电常数为80。在实际岩电实验中所采用的激励电压通常为幅值1 ～5 V的正弦波信号，因此数值模型中在电极间施加幅值为1 V的正弦波交流电压。

2.3 物理模型和求解方法

水与油在模拟岩心孔隙中流动时，两相之间存在复杂的动态相界面。数值模型中采用的界面追踪方法主要有相场法和水平集法［15-16］。其中相场法采用连续的变量来模拟流体流动的不连续现象，能够捕捉两相流动过程中的相界面，对于尺寸较小的几何模型（微流体仿真），相场法比水平集法对界面识别的精确度更高，因此本研究的数值模型采用相场法。通过求解Cahn-Hillard方程实现对两相界面的跟踪［17］，即

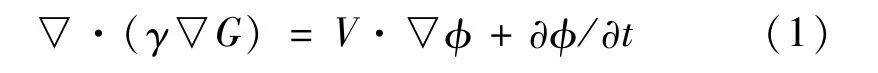
式中：G 为化学势能；γ 为控制Cahn-Hillard 方程扩散尺度的迁移系数；φ为相场参数，表示油时相场参数的值为1，表示水时相场参数的值为－1，表示两相界面时相场参数的值为0。

模拟岩心中流体流动通道尺寸小、流速低，通过计算雷诺数得知模拟岩心中的流态为层流，因此选用层流模型对流场参数进行计算。在微小流道中通常不考虑重力的影响，此时黏性力和惯性力支配着流体在模拟岩心中的流动状态。假设水和油均为不可压缩流体，水与油互不相溶，由流体力学理论得到描述流动过程的动量守恒方程和质量守恒方程［18］：

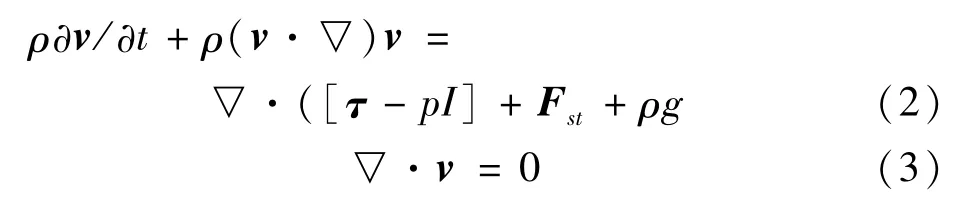
式中：v 为流体的速度矢量，m／s；ρ 为流体的密度，kg／m3；I为单位矩阵，τ 为黏性切应力张量，Pa；Fst为单位体积的界面张力矢量，N／m。

在分析流场与电场耦合问题时，考虑到模型中所采用的电极激励电压幅值较低（如1 V），不足以使油相和水相电离而影响相分布，因此不考虑电场对油水相分布的影响，数值模型中的物理场耦合为流场对电场影响的单向耦合分析。忽略电场中磁效应的影响，由电荷守恒方程得［19］：

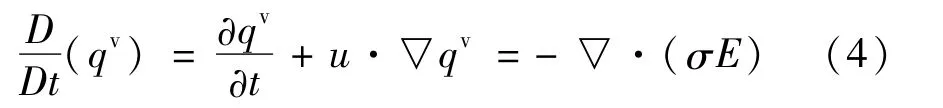
式中：σ为电导率，S／m；qv为体电荷密度，C／m3；u 为流速，m／s；E为电场强度，V／m。

采用MUMPS（Multi-frontal Massively Parallel Sparse direct Solver）算法、瞬态求解器对流场和电场控制方程进行求解，将多孔介质内的流场和电场进行耦合时选用层流物理场接口、相场物理场接口和电流物理场接口。

2.4 网格剖分与选择

由于模拟岩心中流体通道不规则，所以采用自由剖分的三角形网格。网格划分的精细程度影响计算结果的准确度和所需的计算时间，因此需要讨论网格数的影响。针对图2 所示的多孔介质模型，共考察了6种具有不同单元数量的网格，即6 452、12 066、14 408、20 496、28 232 和38 858。以多孔介质模型的入口作为起点（见图2），截取多孔介质x ＝1.5、4.5、7.5、10.5、13.5 mm 5 个截面，由于多孔介质内相分布的变化将导致电场中电势分布的变化，因此选取不同截面处电势的均值来讨论数值模拟结果对网格数量的依赖性。

图3 显示了不同截面处电势均值随网格数变化的曲线。由图可知：当网格数小于20 496 时，电势均值随着网格数的增加而变化，但是当网格数从20 496 增至38 858 时，各截面处电势均值趋于稳定。综合考虑计算结果与计算时间，最终选择网格数为28 232。

图3 各截面处电势均值随网格数变化曲线

3 微观因素对相分布特性的影响

3.1 壁面接触角

润湿性影响模拟岩心孔隙中油／水分布和流动特性，进而影响模拟岩心的电学响应特性。润湿性可通过壁面接触角θ来表示。当θ ＜π／2 时，壁面亲水；当θ ＞π／2 时，壁面亲油。图4 为壁面接触角不同时模拟岩心内的油水相分布图（蓝色代表水，红色代表油）。

图4 壁面接触角不同时的相分布图

分析图4 可知：当模拟岩心颗粒具有亲水壁面时（θ ＜π／2），水以薄膜的状态分布于颗粒表面，注入水易沿着颗粒表面爬行，由于毛管力强，残余油被水圈闭在孔隙中不能流动，其多以簇团状的形态存在；当颗粒具有亲油壁面时（θ ＞π／2），油受到颗粒表面附着力的牵制，油在颗粒表面的流动受到阻碍，弱化了水对颗粒表面油膜的驱替作用，使水在孔隙中形成窜流，在孔隙中多处形成以柱状形态存在的残余油。

3.2 界面张力

界面张力为两不相混溶的液体接触界面产生的力，其大小与毛细管滞留阻力成正比例关系，影响油和水在模拟岩心孔隙中的微观分布形态。将油和水之间界面张力γ12的变化范围设置为1 ～3 mN／m，图5 为界面张力不同时多孔介质内油水相分布图（蓝色代表水，红色代表油）。

图5 不同界面张力时相分布图

分析图5 可知：油水界面张力越大，水的驱替阻力越大；界面张力的增大使得将大油滴分散成小油滴所需的分散功升高，导致油的不连续性增强，水包裹油的现象越明显。

3.3 油水黏度比

油水黏度比的不同会引起驱替过程中主导力的变化，进而影响模拟岩心中油水的流动特性和相空间分布。将油水黏度比M的变化范围设定为10 ～50，图6所示为油水黏度比不同时模拟岩心内油水相分布图（蓝色代表水，红色代表油）。

图6 不同黏度比时相分布图

分析图6 可知：随着油相黏度的增大，水驱替的阻力逐渐增大，模拟岩心孔隙中的油不连续性逐渐增强，相同驱替时间时残余油饱和度随之增加；由于模拟岩心上下不渗透边界的影响，驱替过程中边界处的流量大于中部的流体流量，导致油大部分存在于模拟岩心的中部；随着油水黏度比的增大，油更倾向于以簇团状的形式存在。

4 饱和度对电场响应特性的影响

4.1 电极形状的选择

除了模拟岩心内的流体性质和空间相分布以外，电极的形状和位置也影响电场参数的变化特性。

采用指标参数F 来衡量模拟岩心内饱和单相水时的电场分布的均匀性［20］，F表示为

式中：Emax和Emean分别为模拟岩心内部电场强度的最大值和平均值，V／m。

采用灵敏度S来衡量模拟岩心内测量区域的灵敏场分布［21，22］，S表示为：

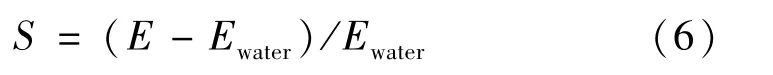
式中：Ewater是模拟岩心内充满水时两电极之间的平均电场强度，V／m；E是驱替过程中某一状态下两电极之间的电场强度，V／m。

综合考虑平板电极和环形电极电场均匀性和灵敏度，以下仅对电场均匀度和灵敏度均较高的平板电极进行讨论。

4.2 基于图像处理的饱和度获取

通过求解数值模型获得不同驱替时刻时模拟岩心中油水的相空间分布图，然后采用图像法对相分布图像进行处理，获得不同时刻时模拟岩心中的含水／油饱和度。通常采用阈值法对相分布二维图像进行处理。

选定RGB（红色、绿色、蓝色）颜色空间，然后根据各颜色分量轴的变化范围设定合理的阈值，当第3 个颜色分量值≥150 时设定为蓝色，其余情况为红色。通过统计各种颜色的像素数量即可得到模拟岩心中的含水／油饱和度。图7 所示为一典型水驱油过程中含油饱和度So随时间的变化图。

图7 模拟岩心中含油饱和度随时间的变化

4.3 含流体饱和度的影响

模拟岩心初始状态为油饱和，此时平板电极与模拟岩心形成一个等效电容器。初始状态时油为连续相，随着实验进程的推进水逐渐进入模拟岩心并将部分油从出口驱出，在某一时刻模拟岩心内部的水成为连续相，此时两平板电极与模拟岩心形成一个等效电阻器。以下将实验过程分为两个阶段进行讨论，即油为连续相和水为连续相。

在油为模拟岩心中连续相的阶段，等效电容器的容抗值受到两个因素的影响，即频率和电容。在电极与模拟岩心尺寸一定的前提下，电容取决于等效介电常数的大小，即受到含油／水饱和度的直接影响。模拟岩心的等效容抗值XC表示如下：

式中：f 为电场频率，Hz；C 为电容，F。在驱替实验的某一时刻，由于油水分布以及含油／水饱和度为一确定值，因此电容C已经确定，则容抗仅受到电场频率f的影响。

图8 为电场频率1 Hz ～1 MHz范围内，模拟岩心中含油饱和度分别为1.000、0.920、0.847、0.755 时的容抗值变化图。分析图8 并结合式（7）可知：随着频率的升高，模拟岩心的容抗降低；在电场频率一定的条件下，含油饱和度越高则模拟岩心等效介电常数越小，导致电容降低和容抗升高，通过测量容抗值即可计算得到模拟岩心中的含油饱和度。

图8 不同含油饱和度时容抗值随频率变化图

在水为模拟岩心中连续相的阶段，等效电阻器的电阻值主要取决于等效电导率，即取决于含油／水饱和度的大小。图9 为电场频率1 Hz ～1 MHz范围内，模拟岩心中含油饱和度分别为0.589、0.553、0.420、0.357、0.255、0 时的电阻值变化图。分析图9 可知：电场频率对模拟岩心电阻值影响很小；当频率一定时，含油饱和度越高则电阻值越大，通过测量电阻值即可计算得到模拟岩心中的含油饱和度。

图9 不同含油饱和度时电阻值随频率变化图

5 结 语

本研究提出了一种基于流场-电场耦合的含水合物模拟岩心岩电数值实验方法，包括模拟岩心建立和电学参数计算两部分。

在构建多孔介质几何结构的基础上进行流场和电场耦合计算。利用水驱油过程所形成的油／水分布来模拟水合物／水的微观分布，通过改变壁面接触角、界面张力、油水黏度比、驱替时间等因素实现对相空间分布和含水合物饱和度的调节，进而建立模拟岩心。利用平板电极在模拟岩心两侧施加1 Hz ～1 MHz频率的交流电场，通过电场计算得到模拟岩心的等效容抗和等效电阻，从而获得宽频率范围的电学响应特性。

所提出的模拟岩心岩电数值仿真方法为含天然气水合物和含油水岩石物理性质的研究提供了新的途径，为物理模拟实验中电学传感器的参数优化、电学测试数据的分析提供了有力工具。