特殊的数列求和方法综述

◇ 甘肃 王 照

本文对特殊数列的前n 项和方法进行归纳,并通过对应例题来展现这些方法的具体应用．

1 拆项求和法

使用拆项求和法首先要求出所求数列的通项公式,再将通项公式分解拆为几个等差数列或等比数列的和或差的形式,然后使用公式法分别求和．

例1求数列5,55,555,…的前n 项和Sn．

解析

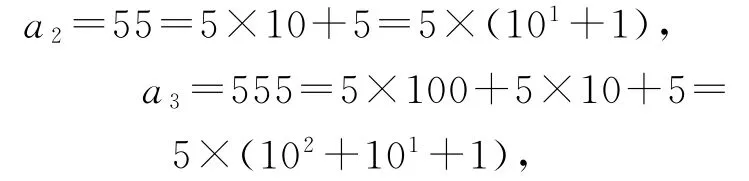
因此,数列5,55,555,…的通项公式为

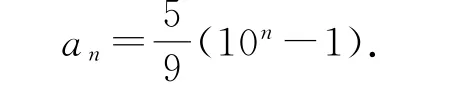
则

2 概率思想

用概率思想求和首先要构造一个概率模型,使相关事件的概率表达式中含有所求和的形式,再结合概率的性质求得其和．

例2求1·2＋2·3＋…＋n(n＋1)．

解析构造概率模型:口袋中有n＋2个球,依次标号1,2,3,…,n＋2,从口袋中任取三个球．记事件Ak为三个球中标号最小的为k．则

根据概率的性质可知

因此,

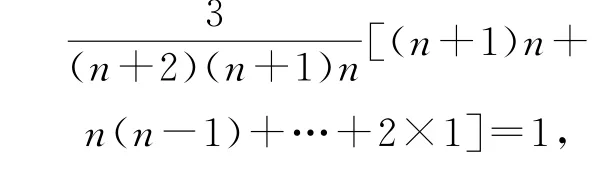
3 导数法

导数法是利用求导公式(xn)′＝nxn－1的逆运算nxn－1＝(xn)′对某类数列求和的方法．

例3在数列{an}中,a1＝1,2an＋1＝(1＋

(1)求数列{an}的通项公式;

解析(1)(求解过程略)．

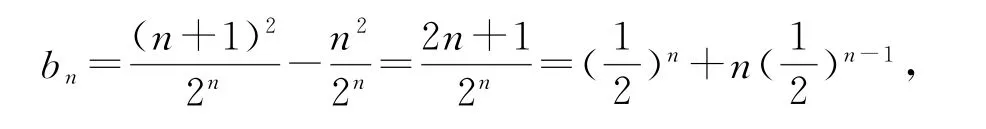
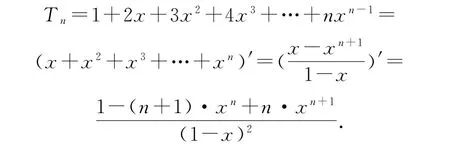
再令从而