一道调研试题的解法探究

◇ 江西 孙 强

1 题目呈现

(1)若函数在x＝1 处的切线与直线ex－y＝0平行,求a 的值;

(2)若f(x)在(0,＋∞)上存在单调递减区间,求a 的取值范围．

这是2020年江西省南昌市高三调研摸底测试卷数学理科第21题,题目结构简洁、设计新颖、层次分明、内容丰富,对于考生运用所学知识寻找合理的解题策略以及运算能力等方面有较高的要求,很好地体现了能力立意的命题原则．历年高考试题都将导数作为高考的压轴题．导数压轴题在考查基础知识的同时,注重对能力、数学思想方法方面的考查,呈现出综合性强、思维量大、方法繁多、技巧性强等特点．

由于第(1)问比较简单,本文仅针对试题第(2)问的解题思路与方法进行一些探究,旨在拓展读者的解题思路,探究问题本质．

2 第(2)问解法探究

解法1(分类讨论)

由题意可知,x∈(0,＋∞)时,f′(x)＝eax＋1－有解．当x∈[1,＋∞)时,f′(x)＝eax＋1－恒成立,不存在单调递减区间．当x∈(0,1)时有解等价于ax＞0有解．

综上所述,a＜－2．

点评在处理不等式问题时,可以将不等式转化为等价的不等式来证明,例如,eax＋1－故只需要证明在(0,1)上有解即可．同时,导数题的第(2)问通常都可以利用分类讨论来解决,在分类时要注意等号在何种情况取到．

解法2(洛必达法则)

由题意可知,x∈(0,＋∞)时,f′(x)＝eax＋1－有解．

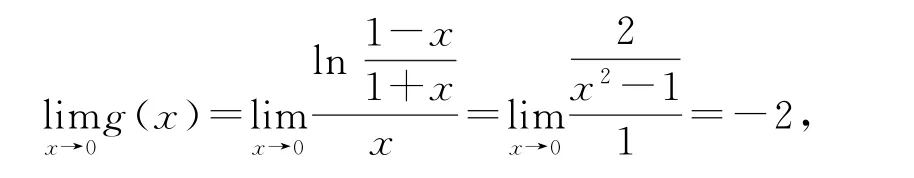
则a＜－2．

点评运用化归思想,将恒成立问题通过参数分离转化为最值问题,再通过最值求参数a 的取值范围,从而避开解法1中对参数a 的讨论,简化证明步骤．

解法3(放缩法)

由题意可知,x∈(0,＋∞)时,f′(x)＝eax＋1－有解．当x∈[1,＋∞)时,f′(x)＝eax＋1－恒成立,不存在单调递减区间．

证明上述命题之前,先证明两个不等式:

①当x∈(0,1)时,令φ(x)＝ln(1－x)－ln(1＋单调递增,φ(x)＞φ(0)＝0,即

必要性:由②可知,当x∈(0,1)时,ln(1－x)－ln(1＋x)＜－2x,故ax＜ln(1－x)－ln(1＋x),则ax＜－2x⇔a＜－2,所以a＜－2是的一个必要条件．

综上所述,a＜－2．

点评利用放缩法证明本题时,容易仅证明充分性而忽略必要性,从而导致回答不全面,所以在利用放缩法证明的时候一定要思考充分性与必要性是否同时满足．要注意在使用放缩的过程中,即使是一些经典的式子,例如1＋x 等,都需要先证明后使用．

教师要重视高考题,充分挖掘和发挥试题的作用及价值,引导学生从不同的思维角度分析问题,领悟不同的解题方法,精学一题,妙解一类,进而提炼出数学思想与方法,实现教学效率的最大化、最优化．