不等式证明的三种经典解法探析

◇ 甘肃 陈 军

求解不等式问题的基本思想是根据不等式的基本性质进行等价转换、同解变形等,这个过程必然要与方程、函数、图象及其他知识相联系,运用分类讨论、数形结合、整体代换等数学思想进行求解．不等式证明问题又是不等式问题中的特殊问题,证明方法纷繁复杂、千变万化、技巧性强．本文就对均值不等式法、柯西不等式法、数学归纳法三种经典求解不等式证明的方法进行例题详解,希望读者能体会其妙用．

1 均值不等式法

例1若a,b,c∈(0,＋∞),求证:

证明已知a,b,c∈(0,＋∞),所以根据均值不等式b＞0),可知

将三式相加,整理得

点评利用均值不等式证明不等式,首先要观察所证不等式的特点,要合理应用裂项、分解、变形等方法,把不等式一侧的项进行分组,每组找到两个大于零的项,再结合题目中所给的已知条件,应用均值不等式结论就可证明所求不等式,要注意,均值不等式只能应用在所有项都是正数的不等式．

2 柯西不等式法

柯西不等式:若ai,bi∈R(i＝1,2,…,n),则

当且仅当ai＝λbi(λ 为常数,i＝1,2,3,…,n)等号成立．常见的变形形式如下．

(1)设ai∈R,bi＞0(i＝1,2,…,n),则

当且仅当bi＝λai(i＝1,2,…,n),等号成立．

(2)设ai,bi同号且不为零(i＝1,2,…,n),则

当且仅当b1＝b2＝…＝bn,等号成立．

例2求证

证明原不等式左边变形得

由柯西不等式得

点评利用柯西不等式证明不等式,首先要对原不等式进行合理裂项、分解、变形等,把不等式某一侧转化为可用柯西不等式的形式,然后利用柯西不等式结论得出结果,再进一步证明结论．

3 数学归纳法

例3已知数列{an}满足且2an＋1·an＋9an＋1－20＝0,请证明:

证明(1)当n＝1时,易知a1＞5成立．

假设n＝k 时,不等式成立,即ak＞5,则当n＝k＋1时,由变形,可得

要证明ak＋1≥5,即使ak＋1－5≥0即可．

由ak＞5,可得2ak－9＞0,ak－5＞0,从而确定ak＋1＞5成立．

综上,对于一切自然数n 都有an＞5成立．

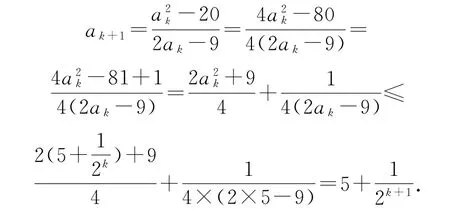
由于ak＞5,故有

点评数学归纳法的精髓在于逻辑的递推过程,首先要确定第1项成立,由已知、基本计算或基础事实求证,假设第k 项成立,然后在此基础上,通过变形、放缩等手段,结合数学基本原理证得第k＋1项成立,从而说明在整个取值范围内成立．用数学归纳法证明不等式只适合于数列不等式．