新型插入式PCB罗氏线圈电流互感器设计

沈映

（云南电网有限责任公司红河供电局，云南 蒙自 661199）

0 前言

传统的罗氏线圈采用手工绕制，绕制工艺繁琐，线圈密度和截面积不均匀，给线圈的准确标定带来困难，批量生产中线圈参数的分散性较大。线圈互感系数的稳定性是实现电流稳定测量的关键技术之一，因此对线圈的绕制必须遵循如下原则：二次绕组在一定大小的非铁磁材料骨架上对称均匀分布；每一匝绕组的形状完全相同；每个绕组的平面垂直于骨架圆周的中心轴[1-3]。

为了解决线圈绕制困难问题，有学者提出了一种新型的罗氏线圈的制作方法[4-5]，即印刷电路板（PCB）平面型罗氏线圈的绕制方法。该方法保证了线圈分布与线圈横截面积的均匀程度，解决了传统罗氏线圈互感系数不稳定问题，提高了线圈测量精度、灵敏度及稳定性。但是受限于PCB的厚度，导致二次绕组磁通大小受限，在实际应用中具有一定局限性[6-7]。

本文结合现有研究，设计了一种插入式的罗氏线圈，解决了PCB厚度对测量精度的影响，通过开口式双回路的设计，使得应用更加广泛，测量稳定性、测量范围得到了明显的改善。

1 新型插入式罗氏线圈

插入式罗氏线圈由一个主板和多个插板组成，如图1所示。该主板用于固定插入式板和电连接插入式板。通常，还布置回线以减小垂直干扰误差。插入式罗氏线圈用于测量电流的原理与普通罗氏线圈和平板罗氏线圈相同：导体上的电流在电路板的线圈中感应出一个电压，该电压与导体电流具有确定的关系，例如微分或线性关系，最终获得感应电压以计算导线上的电流[8]。与平板罗氏线圈相比，插入式罗氏线圈在单个截面上具有更多的线圈，这增加了互感并减小了体积和重量。主板上均匀分布多个插板，各个插板上布置线圈，通过各个插板的串联，将感应电压叠加，该感应电压和被测电流存在对应关系，最终测量得到被测电流大小。

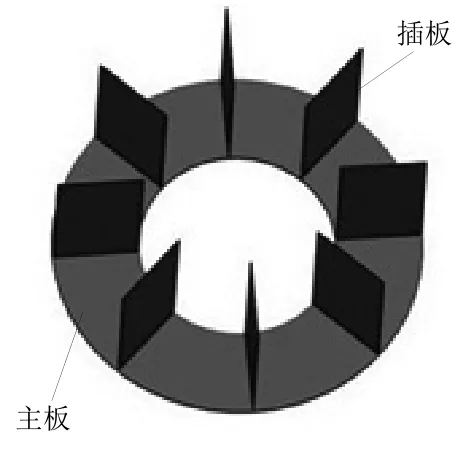
图1 插入式罗氏线圈结构示意图

为了便于计算，电路板上的线圈布线通常是规则的。本文的布线结构如图2所示。参照传统的罗氏线圈自感互感计算方法，计算了插入式罗氏线圈的互感和自感[9]。

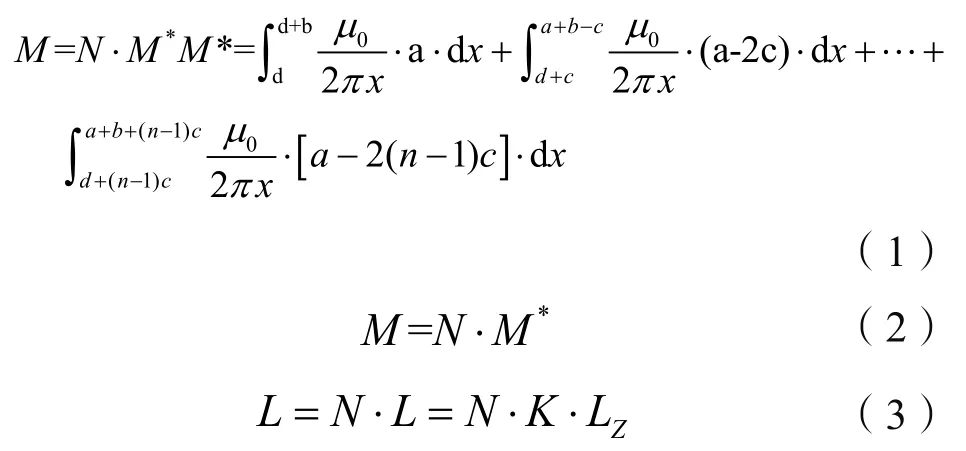
其中d是距母板中心的板边缘的边缘j距离，c是线宽w和线距s之和，n是板上线圈的匝数。N是板数，Lz是每块板的自感系数，K是耦合系数。

图2 插板线圈布局

由图2可知，插入式罗氏线圈电压磁通面积更大，由于PCB印制技术的特殊性，可以将线圈尺寸控制的更加精确，各个插板线圈基本保持一致。结合计算公式（1）（2）（3）可知：其自感系数更大，稳定性更高，尺寸控制更加合理，故测量稳定性及精确度有明显的改善。

2 插入式罗氏线圈开口设计

电流传感器要用在带电校验系统中，需要进行开口处理，在不断开导线的情况下，接入导线进行测量。开口式插板罗氏线圈面临开口误差和开口连线的问题，开口之后，罗氏线圈的互感变化情况，以及开口的距离大小对罗氏线圈的精度影响都需要进行考虑。其次，开口对于主板上的连线提出了要求，设计变得更加复杂。

开口的设计一般将线圈分成两部分，比如两个半圆，装配到导线上时，将两个半圆合在一起，加固之后使用。如下图3所示，A,B为连接处，线圈被分成两个半圆。

图3 开口结构示意图

插入式罗氏线圈设计使得插入式罗氏线圈的主板上有一处没有连线的截面A，这里一般将引线引出来，在此处可以开口。开口如下图4（a）所示。

图4 插板主板开口设计

黑线为分割线，A处为回线设计产生的没有连线的空白截面，对应的B处，也需要进行开口，才能将线圈分开，连线通过焊接导线相连，或者通过其他措施，在B处将导线连接在一起，组装之后使用。

另外一种没有完全分割的设计如图4（b）所示。该开口设计不需要将整块主板切割开，一定程度上保证了参数的准确性。

两种不同设计的误差来源均为两半圆的间距以及开口大小。但是方法一引入了两根导线，方法二的等效回线和连线的参数发生不均等，会在一定程度上影响垂直磁场干扰的消除。

3 误差分析

像平板和常规罗氏线圈一样，插入式罗氏线圈的误差计算还包括偏心误差、倾斜误差、温度误差、干扰误差等。平板罗氏线圈的位置，温度和干扰的误差的计算非常详尽，可以帮助计算插入式罗氏线圈的误差。扁平型罗氏线圈被视为插入式罗氏，板上仅需绕线一圈。 另一方面，该线圈将插入式罗氏线圈看作是许多不同内径和绕组直径的平板罗氏线圈的叠加。从开口偏心误差的角度进行误差分析。

设圆的一半在标准位置，另一半的圆的偏心误差为w。如下图5所示。

图5 开口模型

导线穿过上半圆的中心，上半圆和下半圆之间的间隙为w，即偏心率为W=w。上图中的下半圆使用偏心率算法将角度在-90°～90°范围内的插入线圈相加。

偏心公式中，取离中心点半圆形，角度为90°～270°，互感为：

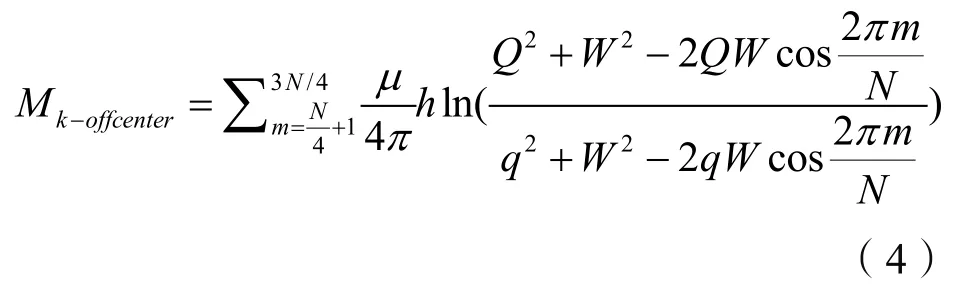
然后对板下线圈数进行积分，得到下半圆的互感为：

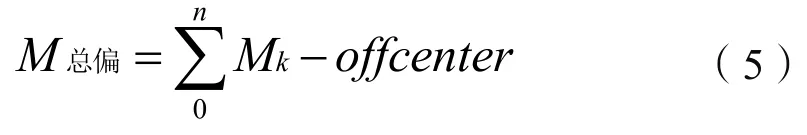
设正常状态下的互感为M，于是误差为：

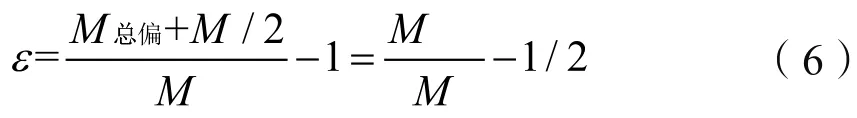
matlab计算得到：

表1 不同间隙距离产生的误差

从上表可以看出，开口式的插入式罗氏线圈的互感精度随着开口距离的变化而变化。如果开口小于0.1 mm，可以认为变化在万分之三以内，如果开口距离太大，在装配试验等过程中，开口距离发生变化，导致互感变化，产生误差。

此时，如果发生其他各种误差，以偏心误差为例，设偏心距为W，开口为w，W和开口处的夹角为θ：对于下半圆，偏心距为W，对下半圆积分：

对于已经有w偏心的上半圆，偏心角度为：

偏心距为

这样，上半圆的偏心互感计算为：

总的互感误差为：

仿真计算可得，80%偏心条件下，不同的θ(弧度)产生的误差如图6所示。

图6 不同开口距离不同偏心角度的80%偏心误差

由以上可见：

1）开口距离的增加显著的增加了80%偏心误差，在没有开口的情况下，偏心的误差几乎可以忽略。

2）相比开口下，导线中心位于下半圆的圆心处的情况，误差有些情况会更大，尤其是角度在0°左右的情况，误差要超过90°情况时将近一倍。

总的来说，罗氏线圈开口偏心距离和偏心角对互感系数影响较大，因此，在进行开口设计时要注意开口尺寸和位置，这样有利于提高测量精度。

4 插入式罗氏线圈功能验证

为了验证插入式罗氏线圈的可行性，利用该技术原理对汇流排电流进行测量，针对汇流排的形状特点，设计了一种新型开口式双回路插入式电流传感器，如图7所示。

方形开口结构设计是为了更好的配合回流排的结构，双回路是为了更好的配合开口式设计，使得设计更为合理，布线更短，并且磁通增加一倍，测量准确度更高。两个回路的首尾连接，使得流过线圈内部的电流在线圈上产生的感应电压叠加，外部的电场在线圈上产生的感应电压抵消，提高了测量精度和抗干扰能力[10]。

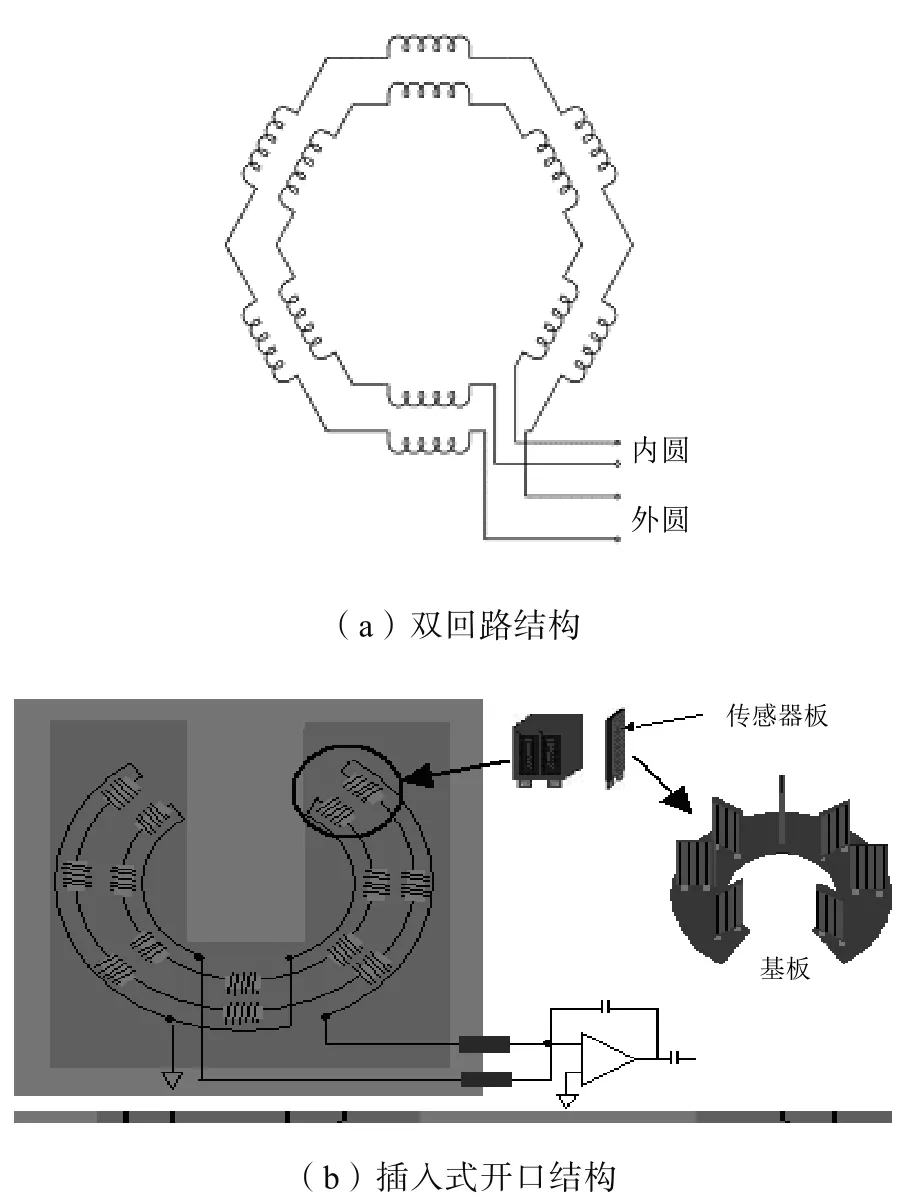
图7 双层结构双回路电流传感器

将该装置、传统罗氏线圈以及标准电流互感器同时安装在汇流排上进行测试，结果表明，该装置能够有效的测量回流排电流大小，且测量准确度比传统罗氏线圈更高。因此，该新型插入式罗氏线圈对于传统罗氏线圈测量效果有所改善。

综上所述，插入式罗氏线圈互感大，重量轻，抗干扰能力和潜力大，内阻小，相比传统罗氏线圈和平板式罗氏线圈，插入式罗氏线圈的自感系数很好，有助于改善测量性能。除了这些优点之外，插入式罗氏线圈在开口方面也有优势，因为很多平板式罗氏线圈一起开口，对齐有很大困难，引入相当的误差。这些足以说明，插入式罗氏线圈在理论上对平板式罗氏线圈有优势，具有广泛的发展前景。

综上所述，该插件罗氏线圈具有互感系数大、重量轻、抗干扰能力大、内阻小等优点。与传统的罗氏线圈和扁平罗氏线圈相比，插入式罗氏线圈的自感系数非常好，能大幅度提高测量性能。除了这些优点外，插入式罗氏线圈在开口方面也有优势，因为许多平板罗氏线圈是一起打开的，对齐非常困难，会带来相当大的误差。这充分说明插件式罗氏线圈在理论上对平板罗氏线圈是有利的，具有广阔的发展前景。

5 结束语

基于目前传统罗氏线圈绕制困难，准确度较差等现状，提出了一种新型插入式罗氏线圈，并阐述了两种不同的开口设计，对开口设计的误差进行了计算，这对于开口设计有借鉴意义。另外，基于新型的插入式罗氏线圈原理，设计了一种用于汇流排电流测量的开口式双回路插入式电流传感器，测试结果表明，该装置具有优异的性能，具有良好的发展前景。有以下结论：

1）插入式罗氏线圈电压磁通面积更大，其自感系数更大，稳定性更高，尺寸控制更加合理，故测量稳定性及精确度相对于传统罗氏线圈有明显的改善。

2）两种不同开口设计各有利弊，全切割引入了两根导线，半切割的等效回线和连线的参数发生不均等，会在一定程度上影响垂直磁场干扰的消除作用。

3）罗氏线圈开口偏心距离和偏心角对互感系数影响较大，因此，在进行开口设计时要注意开口尺寸和位置，这样有利于提高测量精度。

4）设计了一种开口式双回路插入式电流传感器对汇流排进行电流测量，实践证明，插入式罗氏线圈比传统式罗氏线圈和平板式罗氏线圈更有优势，具有广泛的发展前景。