异步联网条件下低频振荡的电力系统稳定器优化方法

高文波，龚小燕

(1. 云南能投有能科技股份有限公司，昆明 650051；2. 云南电网有限责任公司培训与评价中心，昆明 650204)

0 前言

大容量、远距离直流输电技术在电网中的广泛应用，减少了系统的阻尼[1-7]。

文献[8-9]从调速系统的角度阐述了云南电网低频振荡产生的原因。文献[10]考虑了直流频率控制功能（FLC）与系统之间协调控制的影响。文献[11-12]讨论了云南异步联网之后低频振荡的影响及相关措施。文献[13]论述了采用GPSS抑制系统低频振荡的特点。

电力系统稳定器(PSS)经过实践证明是解决目前我国大电网联网情况下伴生的低频振荡问题的有效解决手段，其对系统低频振荡的抑制作用主要取决于其参数的合理整定，均采用相位补偿参数和主回路增益分别整定的方法。其中，相位补偿参数三个通用导则均规定了相同的功角-10°至45°的补偿范围要求，所有的整定参数只需满足该范围要求即可；主回路增益采用取临界增益系数的1/3至1/2；其他未进行明确的要求。目前电厂机组投产初期，电网调度部门要求的机组电力系统稳定器试验及参数整定即普遍按照以上模式进行。

但现有的PSS参数整定方法值考虑了系统的功角补偿，并没有考虑对其角速度进行补偿，可能会降低系统的最大传输容量，限制系统的能源外送能力。提出了新的PSS综合增益系数计算方法，提高了系统在低频段的阻尼系数，通过实际现场试验验证了该优化方法的有效性，提高了实际系统的电力外送能力。

1 电力系统稳定器原理及分析

根据电力系统稳定器的工作原理，其对电力系统低频振荡的阻尼效果，主要取决于主回路考虑相位补偿时间后的等效放大倍数在图1中的纵坐标角速度轴上的分解量。目前电力系统中普遍采用的电力系统稳定器模型为PSS2B模型图2，该模型结构在励磁调节中固化，换言之，同一发电机组在理论上可以整定多组参数，但是在现场只能采用唯一一组电力系统稳定器参数。

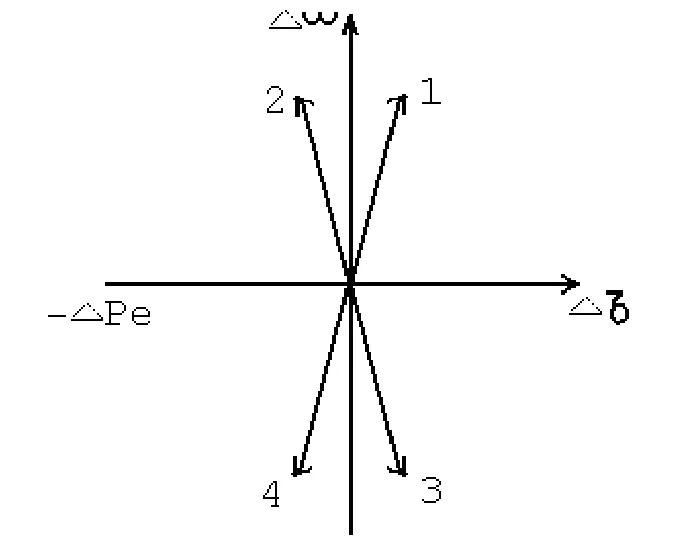
图1 电力系统稳定器工作原理示意图

图1中，具体符号为：Δδ为功角轴；Δω为角速度；以坐标原定为起始点，向量1、向量2、向量3和向量4分别代表电力系统稳定器所附加的力矩的向量示意图。

图2，电力系统稳定器PSS2B模型中，具体的符号为：s为数学领域中传统的拉普拉斯变换因子；Tw1、Tw2、Tw3、Tw4为电力系统稳定器角速度和电功率两个输入通道的隔直时间常数；Ks2为电力系统稳定器电功率输入通道的功率惯性环节的放大倍数；T7为电力系统稳定器电功率输入通道的功率惯性环节的惯性时间常数；Ks3为电力系统稳定器中转子机械转矩计算中所需的电功率部分的放大倍数；T8、T9分别为电力系统稳定器中陷波器的分子和分母时间常数，M、N为该陷波器对应的分母阶数和分子阶数；Ks1为电力系统稳定器主回路增益系数；T1、T2为电力系统第一级相位补偿用超前、滞后时间常数；T3、T4为电力系统第二级相位补偿用超前、滞后时间常数；T5、T6为电力系统第三级相位补偿用超前、滞后时间常数；Usmax为电力系统稳定器输出最大限幅值；Usmin为电力系统稳定器输出最小限幅值；Us为电力系统稳定器输出信号。

一方面在现有标准下只是采用单机无穷大的试验方式对相关参数进行计算；另一方面，电网结构及规模的扩大必然导则系统振荡模式的改变，而满足电厂投产初期电网振荡模式阻尼要求的电力系统稳定器整定参数随着电网的发展，开始逐渐的由于系统振荡模式的改变而开始出现不能满足电网动态稳定计算指标的要求的情况，甚至出现由于系统动稳能力不足而导致局部电网电力外送受限问题，在此情况下，对结合电网系统计算结果，对电力系统稳定器参数开展优化整定工作就成为势在必行的工作。

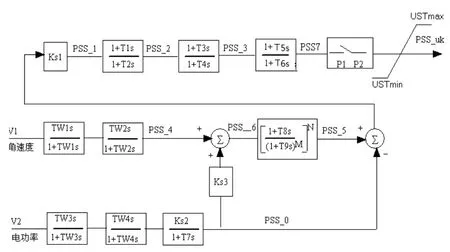
图2 电力系统稳定器（PSS-2B模型）

在电力系统稳定器参数整定过程中，必须将系统所关注的振荡模式和本机振荡模式结合，但是考虑到现场试验时系统所关注的振荡模式的阻尼效果通常无法现场验证，现场扰动仅仅能够验证本机振荡模式的阻尼效果；同时考虑到现场如果仅仅保证本机振荡模式的阻尼效果，电力系统稳定器整定参数可以有多种组合，每种组合在系统所关注的低频段呈现出较大的差异，而按照目前普遍采用的现场整定方法，系统所关注的低频段仅仅考虑其相位补偿效果，在此情况下，根据图1的示意图可以看到，在同一频率点下，相同的电力系统稳定器主回路增益由于相位补偿的差异，其在角速度轴上的分解量可能差异较大，而该部分差异可能导致电网局部地区动稳水平不足，从而影响电网对局部中、小水电的电力外送能力，该现象在目前我国的云南、四川等地的局部地区中、小水电送出受限问题中体现的非常明显。

为此，非常有必要在目前电力系统稳定器现场参数整定过程中，通过定义相应的整定参数的评价指标，尤其是低频段的评价指标，将电力系统稳定器的相位补偿环节和主回路的增益加以结合，综合评估电力系统稳定器整定参数的优劣性，尤其是系统所关注的低频段的优劣性，对解决目前我国局部地区中、小水电由于动稳水平不足而面临的送出受限问题的解决将具有非常现实的意义。

2 励磁系统综合增益系数计算

根据以上分析，非常有必要在目前电力系统稳定器现场参数整定过程中，通过定义相应的整定参数的评价指标，尤其是低频段的评价指标，将电力系统稳定器的相位补偿环节和主回路的增益加以结合，综合评估电力系统稳定器整定参数的优劣性，尤其是系统所关注的低频段的优劣性。因此，本文提出励磁系统综合增益系数计算方法。

电力系统稳定器PSS-2B模型图2中，其相位补偿环节需要考虑PID各个环节，分别计算各个环节在电力系统稳定器工作频段范围内的幅频和相频情况：在此过程中，假定以上各个环节在电力系统稳定器工作频段范围内的各个频率点的幅值和相位分别为：

根据以上计算结果，根据图1的电力系统稳定器工作原理图，将以上得到的电力系统稳定器总体增益按照相位补偿效果进行向量分解，即将电力系统稳定器总体增益KPSS_2B按照相位补偿效果分解到角速度轴和功角轴，此时得到的角速度轴分量即为电力系统稳定器真正其作用的部分，在此单独定义该分解量为电力系统稳定器性能评价参数K，其计算过程如下：

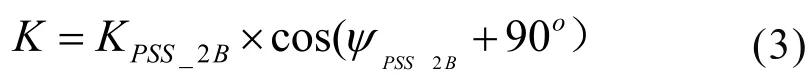
按照以上计算过程，对每一个频率点开展如上的计算，即可得到电力系统稳定器在整个工作频率带范围内各个频率点的综合增益系数K。

根据以上计算结果，针对电力系统稳定器试验现场所提供的各组电力系统稳定器参数，计算得到的电力系统稳定器综合增益系数K，然后画出各组参数所对应的电力系统稳定器工作频段范围内的综合增益系数图；在此过程中，结合电力系统计算所得的所关注的振荡频率点，根据其大小，即可以明确的筛选出对系统最有利的电力系统稳定器整定参数，以满足现场试验的要求。

3 实际算例分析

本次苗尾电厂PSS参数优化问题基于以下原则进行，即：以现有PSS参数中本机振荡模式下的综合放大倍数不变为基本原则。根据现场实际，机组正常运行情况下的机组有功波动频率为本机振荡模式下的频率，且原参数在本机振荡模式下的综合放大倍数考虑为现场所能够接受的最大值，在PSS参数优化过程中保证本机振荡模式下的PSS综合放大倍数不变，通过优化其余参数(T1、T2、T3、T4、T13、T14以及Ks1参数)，考虑系统方式计算中苗尾电厂所参与的滇西北对滇西南振荡频率为0.525 Hz的振荡模式，以及保山对丽江振荡频率为0.606 Hz的振荡模式，以达到最终优化的目的。

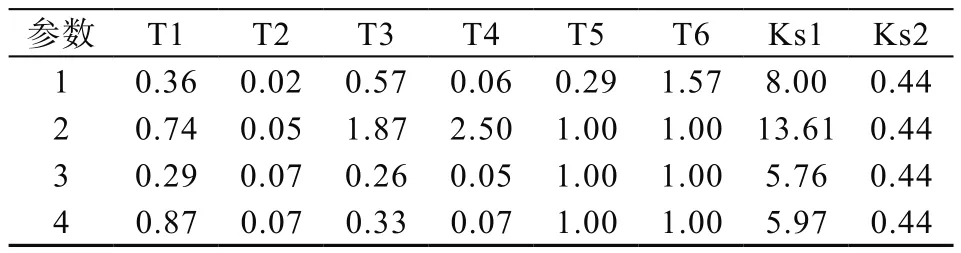
表1 补偿参数

可以看出，优化参数因为采用弱化高频段以提高机组临界增益优化原则，现场参数相位补偿效果略优于其他三组参数，但均满足相关规程要求。

在云南电网苗尾水电厂PSS参数整定现有参数的基础上，分别开展了相关的整定研究及现场研究工作。

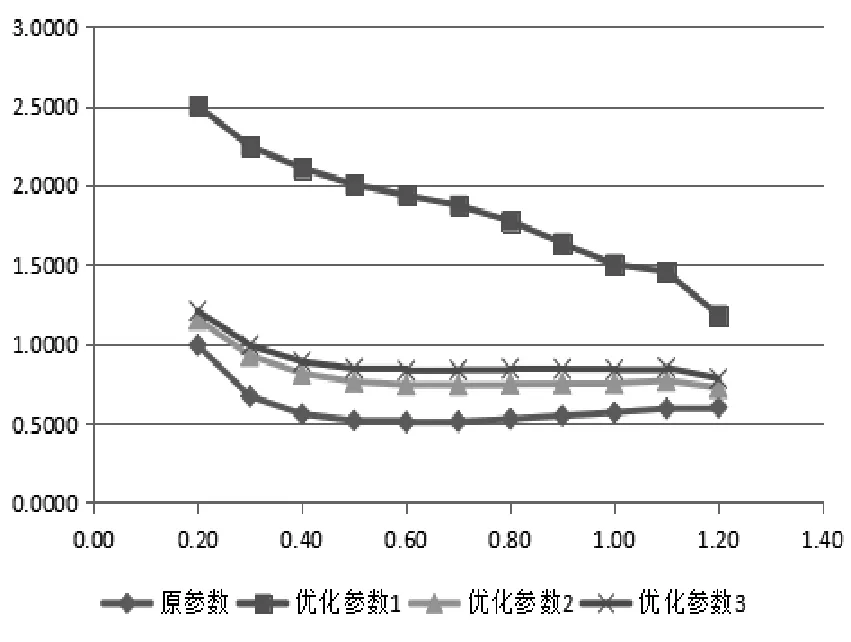
图3 综合放大倍数图

综合比较各组参数，在本机振荡模式下PSS综合放大倍数保持不变的情况下，单独分析低频率段，优化参数1、优化参数2和优化参数3综合放大倍数均优于现场参数，尤其是优化参数1，在苗尾机组所参与的振荡模式中，0.5-0.6 Hz的综合放大倍数是现场参数的3-4倍；优化参数3在同样三级补偿的前提下，通过弱化高频段的相位补偿效果，在0.5-0.6 Hz频带范围内的综合放大倍数相较现场原参数提高了近30%。通过该方法，增加传输通道容量112.3 MW，提高丽江片区的稳定能力。

4 结束语

本文根据云南电网异步联网后系统局部电网所面临的动稳问题，提出了PSS参数的优化整定过程中，适当弱化本机振荡模式的相位补偿，并在此基础上整体提高PSS主回路的整体放大倍数以保证本机振荡部分的阻尼效果，根据PSS在系统所关注的低频段的综合放大倍数按照频段进行选择，得出结论如下：

1）三组优化新参数对本机振荡模式的阻尼效果均明显好于原参数；

2）三组优化新参数对本机振荡模式的阻尼效果差异较小，单从本机振荡模式分析，选择三组优化的任何一种均可；

3）三组优化新参数中第一组的无功反调量相较原参数和优化新参数二和优化新参数三偏大，但是均在规程要求的范围内；

4）三组优化新参数对本机振荡模式的阻尼效果和反调效果均能够满足规程要求，选择标准将唯一取决于其对系统关注的低频段的阻尼效果。