绕管式换热器壳侧冷剂流体均配性能模拟研究

鹿来运，姜益强，汪耀龙，花亦怀，刘凯月，郑文科

(1.中海石油气电集团有限责任公司，北京 100027；2.哈尔滨工业大学 建筑学院，黑龙江 哈尔滨 150090；3.寒地城乡人居环境科学与技术工业和信息化部重点实验室，黑龙江 哈尔滨 150001)

0 引言

大型陆上LNG液化工厂和浮式LNG液化储存工艺中的主低温换热器主要为绕管式换热器[1]，其结构是在中心筒上用小直径管以螺旋状进行缠绕，然后安置于壳体中，换热器的外筒、缠绕管束和封头构成了壳侧空间[2]。通常，天然气在管侧由下向上流动被液化，冷剂在壳侧由上向下流动提供冷量[3]，壳侧空间集中了主要热阻，壳侧冷剂流体的流动对换热器的换热性能有显著的影响，两相冷剂流体分配不均会使换热管之间产生热应力，影响设备寿命，更重要的是会严重影响换热器的换热性能，造成LNG液化工厂运行安全问题，因此有必要对绕管换热器壳侧流体的均配特性进行研究。

国内外对绕管式换热器流体均配性研究较少，而对板翅式换热器的流体均配性进行了大量的研究。Lalot[3]进行实验与模拟研究，发现流体不均匀流动造成的换热效率损失会超过25%。张哲[4]通过实验研究发现两相流分布不均匀程度比单相流更大，换热效果更差。入口结构不合理是造成流体分配不均的重要原因，主要包括封头和导流片两部分结构，两者对流量均配性的影响方式不同。焦安军[5]发现导流片对均配性的影响是在总管流动方向上。张哲[6]发现封头主要影响出口截面横向的流体均配性。许箐[7]研究发现气体雷诺数及干度对均配性具有较大的影响，且液相不均匀度大于气相，横向不均匀度大于纵向。焦安军[8]、张哲[9]、朱建鲁[10]、张冰[11]、陈杰[12]、曹学文[13]等分别研究了封头结构对流体分配的影响，各自提出了改进的封头结构。吴裕远[14]提出对两相流体采取“先分配、后混合”的方法可以达到流体均配的效果。袁培[15]、李焱[16]分别基于该思想提出了各自设计的均流器结构，并证实了均流器对提高流体均配效果的作用。

对于绕管式换热器，常在壳侧入口设置均流器，以达到均配两相流量的目的。鹿来运、郑文科分别设计了盘形[17]、环形[18]及分布管式均流器[19]，并研究了海上晃动参数对均流器均配性的影响。Noé-Landry-Privace M’Bouana等[20]利用VOF两相流及Realizablek-ε湍流模型，研究了环形均布器模型在不同运行条件下的均布性能。模拟结果表明：随着气相入口速度的增大，环形均布器的液相均匀性先变好后变差；随着液相入口压力的增大，环形均布器的液相均匀性得到改善。但是，这些研究针对的是均流器的部分模型，而且研究的是均流器出口即缠绕管壳程入口的流体分配情况，不能反映壳侧流体流经缠绕管处的均配情况。在不同的流量及干度条件下，壳侧流体的均配规律会有所不同，因此本研究将对全尺寸的绕管式换热器整体模型的壳侧流体均配特性进行模拟研究，得出不同流量及干度条件下换热器壳侧流体均配规律。

1 计算模型

1.1 几何模型

使用Solidworks软件建立换热器模型如图1所示，包括环形均流器，缠绕管及外壳三部分。两相流体进入换热器，其中液相进入均流器中芯筒、经由支管、环管，从环管上的小孔流出，实现对液相的均配作用，气相冷剂在均流器外侧流动，与从小孔流出的液相冷剂重新混合后进入缠绕管壳侧空间，从底部出口流出。出口划分为32个测量通道，划分方式及编号如图2所示。

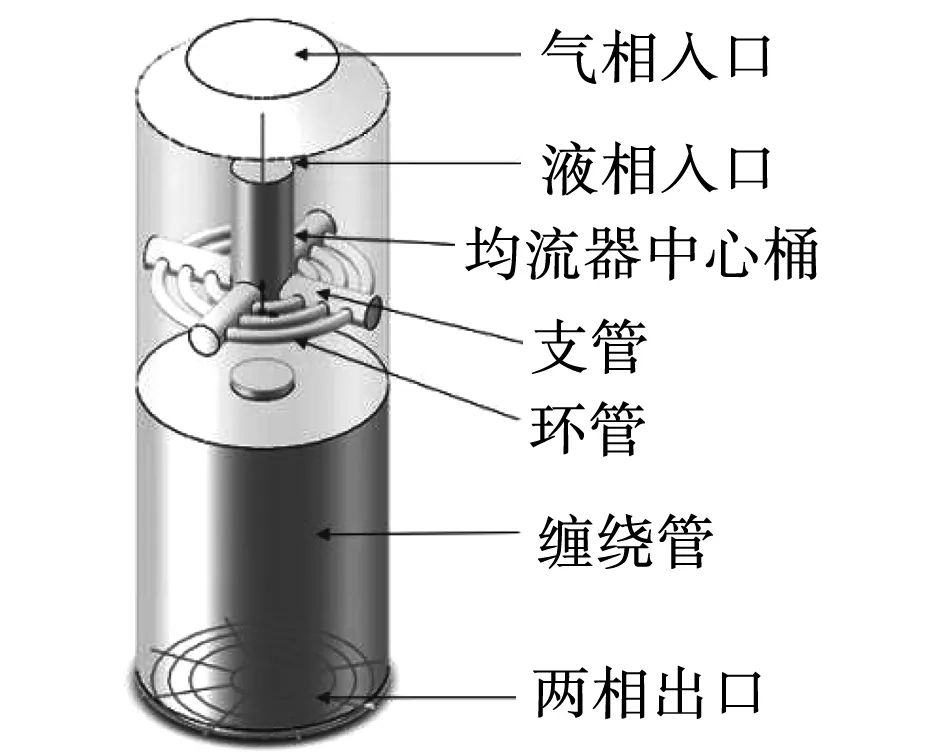
图1 换热器几何模型

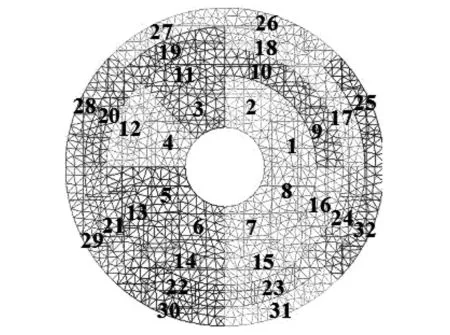
图2 测量通道划分及编号

1.2 网格划分及无关性验证

使用ICEM软件生成了非结构化网格，对均流器区域、缠绕管区域及外壳空间分别创建了BODY，划分为三个不同的域，代表了均流器液相区、缠绕管多孔区域以及壳侧空间的气液两相区，生成的网格如图3所示，均流器环管开孔位置与数量如图4所示。

图3 换热器模型网格划分

图4 环管开孔位置

1.3 模型设置及验证

仿真模型的设置和边界条件的选取如表1和表2所示。

表1 模型选取与算法设置

表2 边界条件设置

冷剂模拟工质物性参数如表3所示。

表3 冷剂工质粘度及密度表

建立三个不同网格数目的绕管式换热器模型进行网格无关性验证，网格数分别为150万、200万和300万，对气相入口流量为0.085 kg/s(即250 m3/h)，液相入口流量为0.244 2 kg/s(即0.88 m3/h)的工况进行模拟，得到各通道两相质量流量比例系数如图5所示，使用200万网格和300万网格计算的结果相差不大，考虑到计算效率等因素，选择网格数为200万的模型进行后续的模拟研究，网格采用四面体网格，网格的最大尺寸为20 mm。

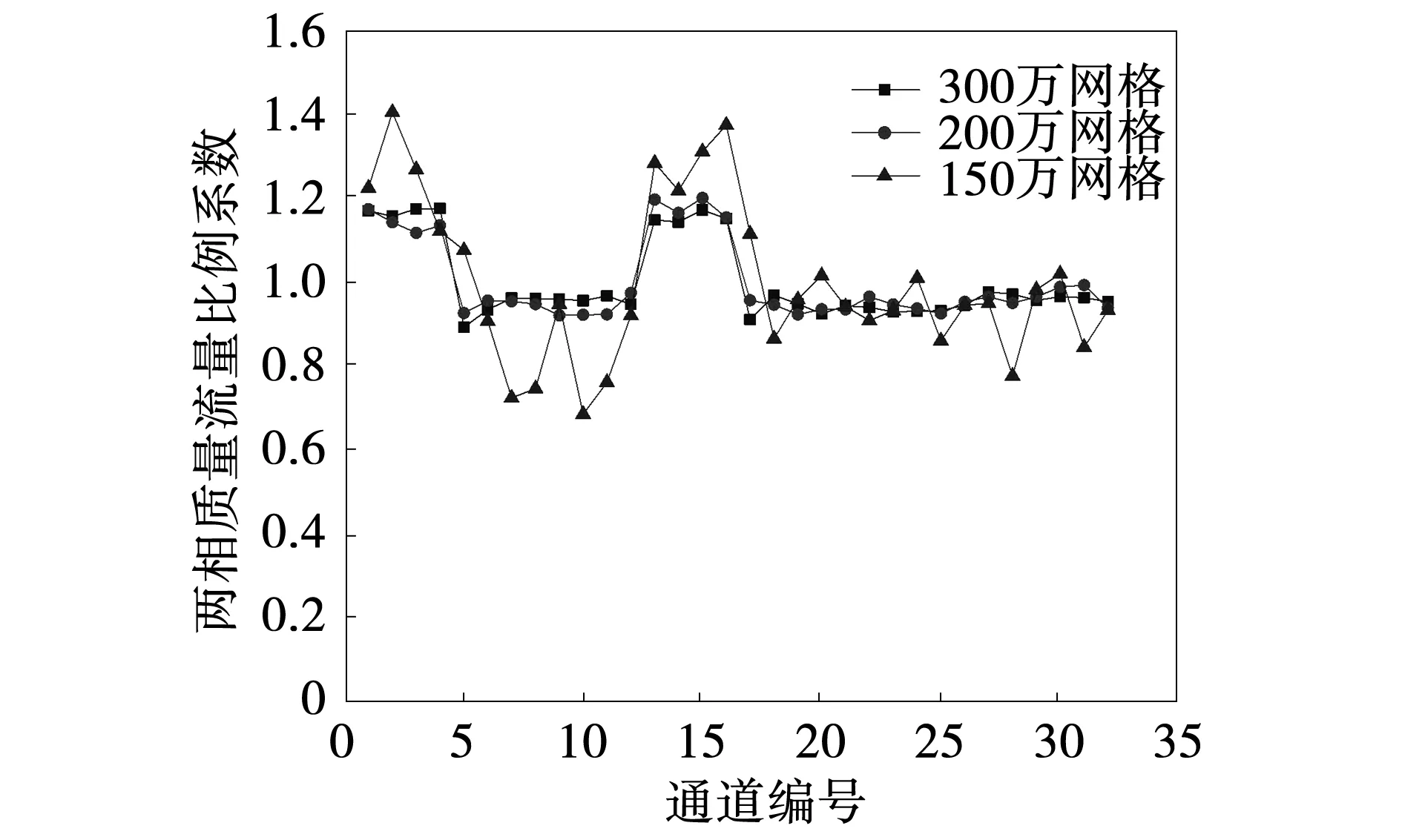
图5 网格无关性验证

为了保证模型的可靠性，采用实验数据验证仿真模型。以空气水为介质，测量12个通道的质量流量，计算绕管式换热器壳侧流体分布的比例系数，如图6和图7所示。模拟工况和实验工况的两相质量流量分布规律基本一致，可见各测量通道的质量流量的实验值和模拟值结果相近，验证了计算模型的可靠性。

图6 工况1比例系数对比图

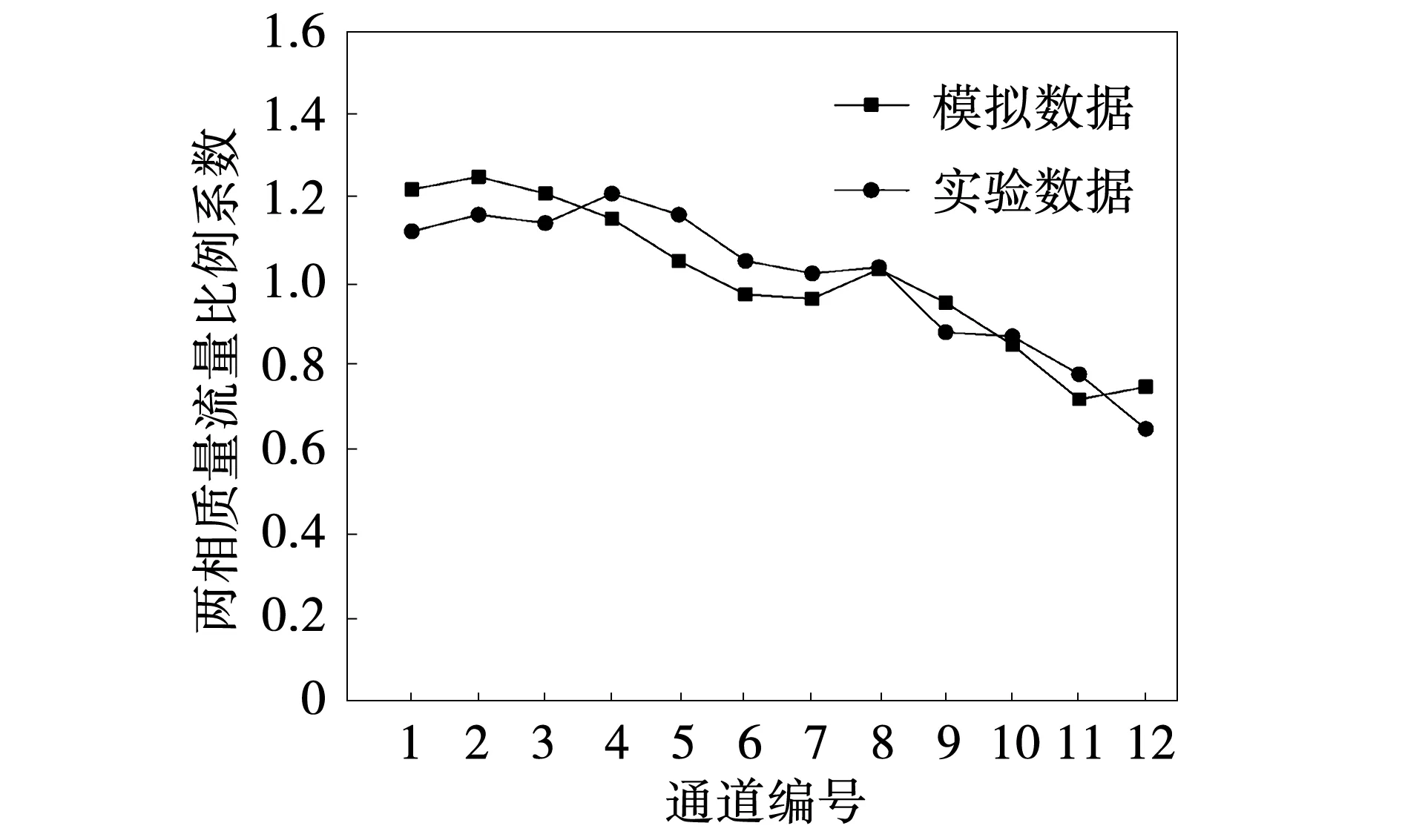
图7 工况2比例系数对比图

1.4 缠绕管多孔区域设置

缠绕管采用多孔区域模型进行模拟计算，多孔区域的设置主要包括孔隙率、粘性阻力以及惯性阻力，孔隙率为孔隙体积与总体积的百分比，实验模型中缠绕管直径为12 mm，层间距为14 mm，共13层，则计算得出孔隙率为0.14。

对于湍流流动，渗透率和惯性阻力系数可使用式(1)和式(2)计算

(1)

(2)

式中α——渗透率/m2；

C2——惯性阻力因子/m-1；

Dp——粒子平均直径/m；

ε——空腔比。

计算得粘性阻力1/α=2.41×108m-2，惯性阻力C2=9.141 m-1。

2 模拟结果分析

2.1 流动均配性评价指标

采用比例系数及离散系数为评价指标。

(1)比例系数：通道流量与平均流量之比

(3)

式中Ki——通道i流量与平均流量的比;

Qi——通道i的流量/m3·h-1;

(2)离散系数：各通道流量相对标准方差

(4)

式中S′——离散系数;

N——通道总数。

比例系数可反映各通道流量的相对大小，离散系数可反映流量整体均配程度。

2.2 总质量流量对均配性影响结果分析

分别保持干度为0.3、0.4、0.5、0.6不变，研究壳侧冷剂流体均配性随两相质量流量的变化规律，在此工况范围内，壳侧两相流体流速满足实际工程的流速范围。

(1)干度为0.3的一组模拟工况

图8为各工况两相质量流量离散系数对比图，可见干度为0.3时，离散系数随流量增加而减小，即分布更加均匀。为了清晰地表示各通道流量分配情况，选取了具有代表性的12个通道进行比较分析，图9为各工况下选定的12个测量通道的质量流量比例系数图，曲线向中间凹陷，分布规律为径向上内、外圈两相质量流量分布较中间圈多。

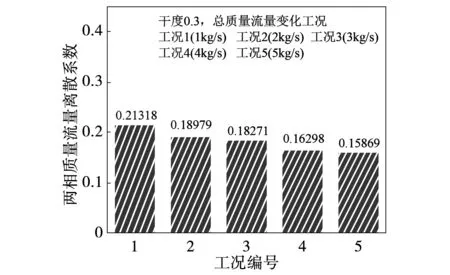
图8 各工况离散系数对比柱状图

图9 各工况通道比例系数折线图

(2)干度为0.4的一组模拟工况结果分析

图10为两相质量流量离散系数对比图，干度为0.4时，离散系数随流量增加而减小，分布更均匀。图11为测量通道质量流量比例系数图，曲线向中间凹陷，流量分布规律为径向上内、外圈质量流量分布较中间圈多。

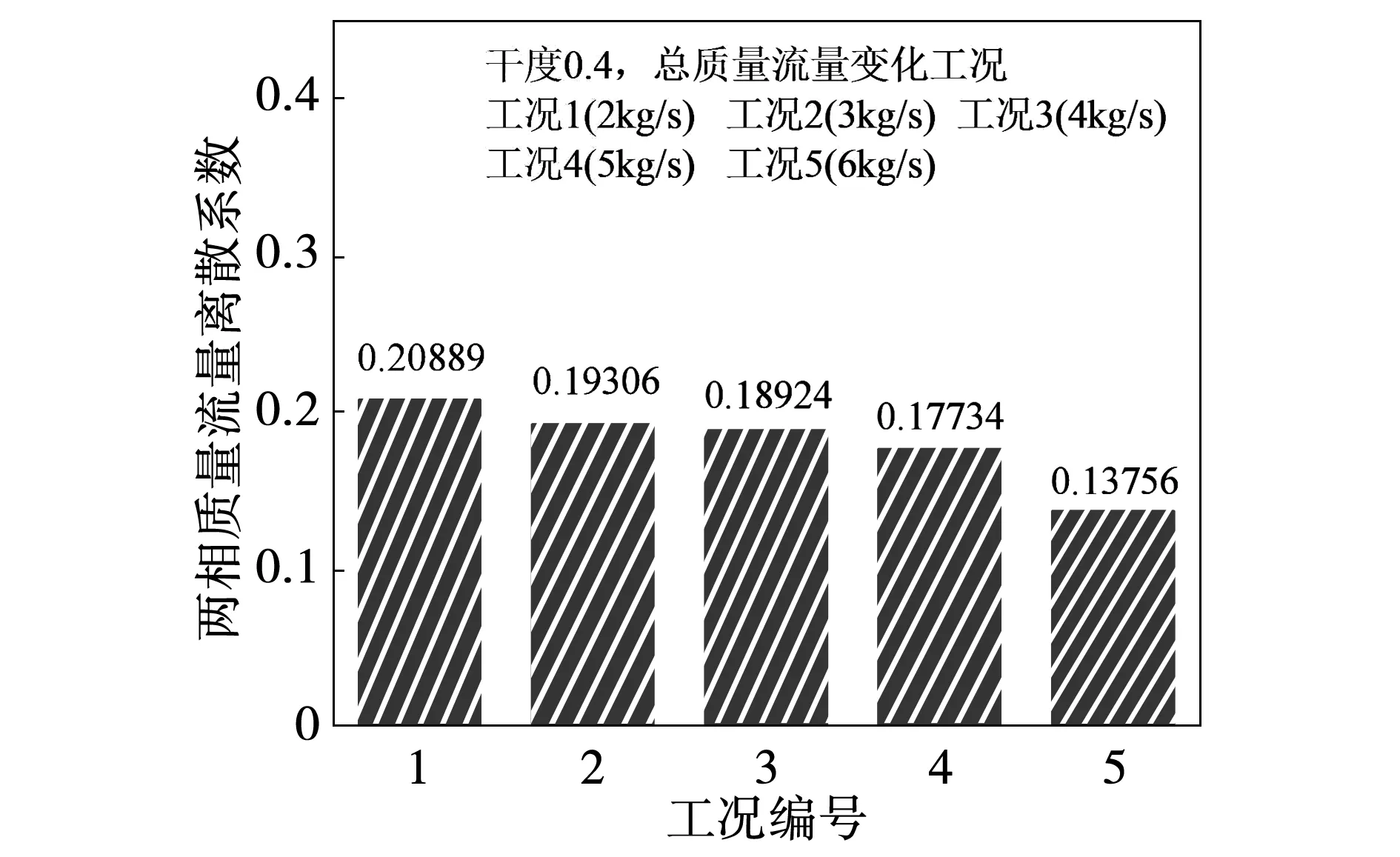
图10 各工况离散系数对比柱状图

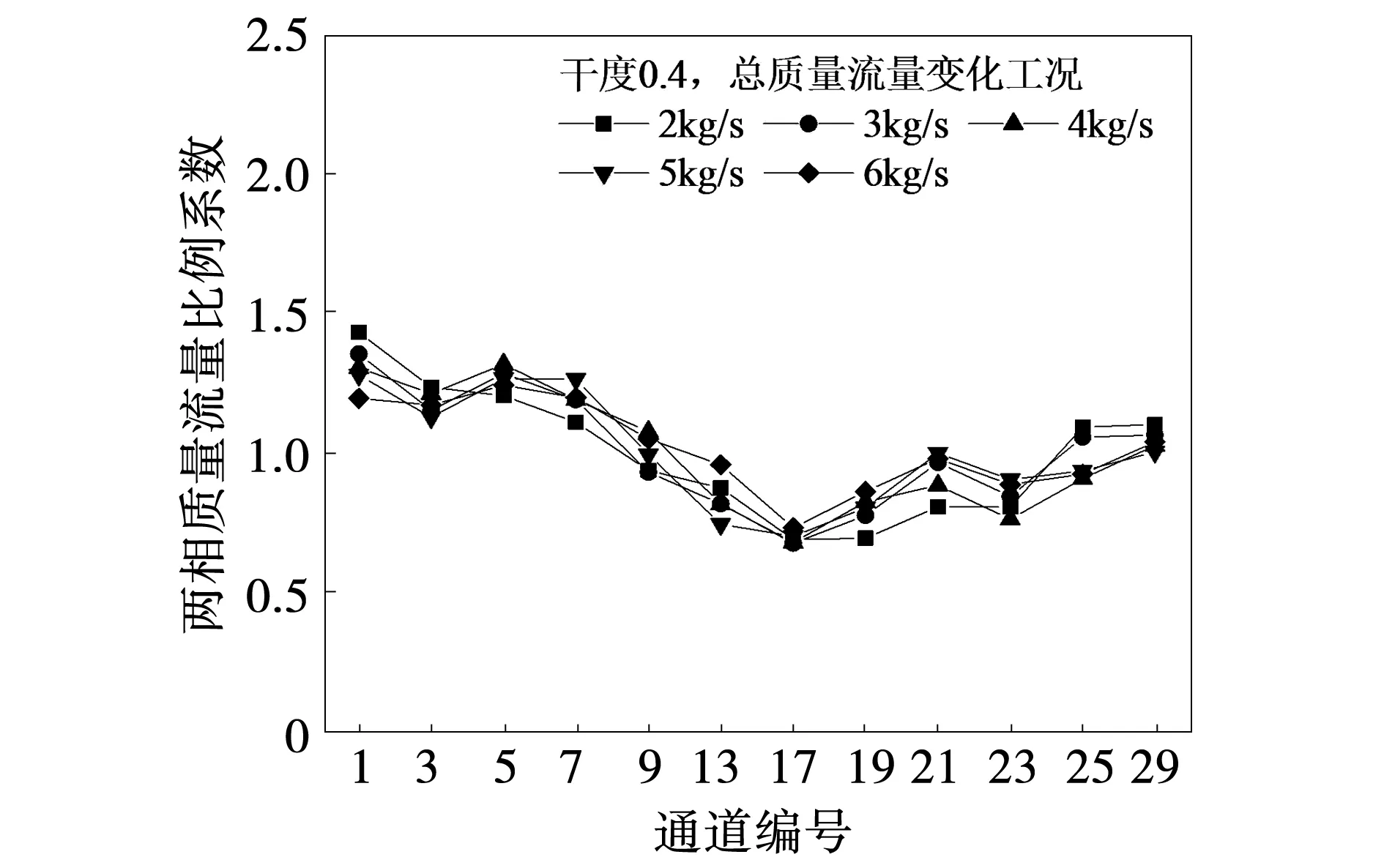
图11 各工况通道比例系数折线图

(3)干度为0.5的一组模拟工况结果分析

图12为离散系数对比图，干度为0.5时，两相质量流量离散系数有随流量增加而减小的趋势，但基本保持稳定。图13为测量通道的流量比例系数图，流量分布规律为周向上流量分布均匀一致，径向上最内圈流量最多，外面三圈流量分布大致相同。

图12 各工况离散系数对比柱状图

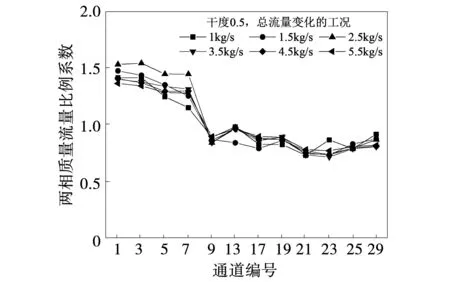
图13 各工况比例系数折线图

(4)干度为0.6的一组模拟工况结果分析

现阶段，云计算的应用主要被分成三类，其分别是私有云、公有云和混合云计算模式。私有云、公有云和混合云计算模式适用条件以及适用时期各不相同，所以私有云、公有云和混合云计算模式应用所产生的效用也存在着很大的差异性。

图14为离散系数对比图，可看出干度为0.6时，离散系数随流量增加而减小，但变化较为平稳，减小趋势不明显。图15为通道质量流量比例系数图，可见流量分布规律为径向上由内至外质量流量减少，最内圈流量最多，第二圈次之，第三圈和最外圈流量分布较少；周向上流量分布均匀。

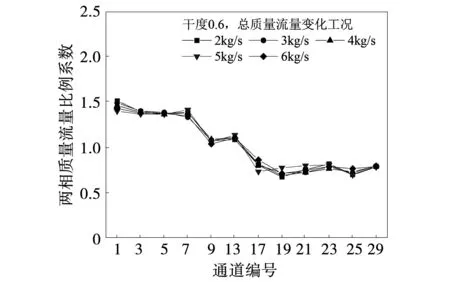
图15 各工况通道比例系数折线图

图16显示了气相流量为1.2 kg/s，液相流量为0.8 kg/s，干度0.6的工况1下，壳侧空间及均流器内冷剂的流速分布。计算各工况下通道的质量流量平均比例系数，可以定量比较径向上的流量分配差别。干度为0.3和0.4时，中间两圈平均流量约为内外圈平均流量的1.3倍；干度为0.5和0.6时，两相质量流量分布规律为径向上由内至外流量减少，最内圈流量约为最外圈流量的1.7倍。

图16 壳侧空间气相及液相冷剂流速分布

2.3 干度对均配性影响结果分析

分别保持两相质量流量为2 kg/s、3 kg/s、4 kg/s、5 kg/s不变，研究壳侧冷剂流体均配性随干度的变化规律，表4中列出了干度变化的各组工况的模拟结果：对表5所列的4组工况的模拟结果分析，可见质量流量不变时，两相质量流量离散系数随干度增加而增大，均匀性恶化。

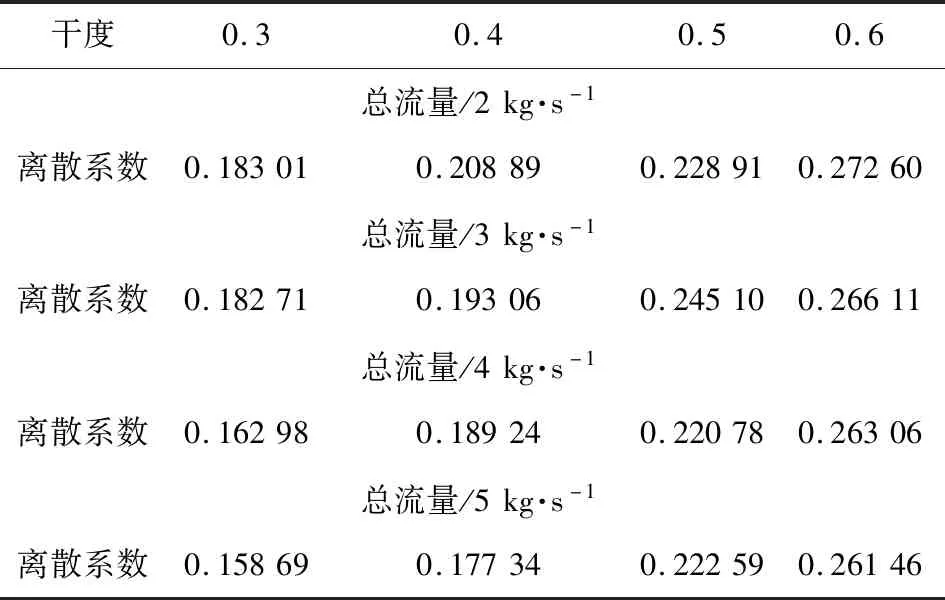
表4 质量流量不变，干度变化工况的模拟结果表

3 结论

本研究建立了绕管式换热器数值模拟模型并利用实验数据进行了验证，以冷剂为工质进行两相流模拟研究，得出如下壳侧冷剂工质两相流动均配规律：

(1)干度不变时，绕管式换热器壳侧两相冷剂流体质量流量分布随流量增大而更均匀，干度小于0.5时均配性变化趋势明显，干度大于等于0.5时变化幅度较小；

(2)质量流量不变时，流体分布随干度减少而更均匀；

(3)干度大于等于0.5时，流体分布在径向上由内至外质量流量减少，最内圈流量约为最外圈流量的1.7倍；

(4)干度小于0.5时，径向方向上内圈与外圈质量流量分布较中间圈多，中间两圈平均流量约为内外圈平均流量的1.3倍。