基于双流体模型的喷动-流化床不同流动形态的模拟研究☆

赵俊楠,王会宁,戈朝强,刘国栋

(1.哈尔滨工业大学 能源科学与工程学院，黑龙江 哈尔滨 150001;2.北京航天动力研究所,北京 100076)

0 引言

在喷动床(Spouted Bed)中，高速喷动的气体通过喷嘴喷入床体，形成高速射流，射流携带颗粒喷动至一定高度，颗粒受到重力作用，在达到最高处之后向床体两侧自由下落，进入环状回流区，受到高速射流的夹带再次向上喷动形成循环。由于大尺寸颗粒可以在喷动床中取得较好的流化效果，因此被广泛应用于农作物干燥、生物制药等重要领域。但是，这种床型在床底两侧会形成不流化不流动的“死区”。喷动-流化床(Spout-fluid Bed)的出现，显著提升了床体两侧的流化程度，原先“死区”内部的颗粒被充分流化起来，得到了更为广泛的应用。目前，喷动-流化床技术在煤气化过程中扮演着重要角色，成为煤气化技术的主要炉型之一。除此以外，在农业生产、生物制药等多个领域，喷动-流化床技术也有相当广泛的应用。

近年来，国内外的专家学者已经对喷动-流化床进行了深入而广泛的研究。但对其流动结构以及动力学参数的掌握依然不够系统，在工业放大和实际应用等过程中仍然有一定困难。因此，本文的研究目的在于运用双流体模型研究喷动-流化床内不同流动结构下的气固两相流动特点，探讨两相的浓度、速度以及脉动速度的分布规律。

长期以来，很多学者采用不同方法对气固两相喷动流化系统进行了研究[1-3]。沈来宏等[2]采用实验方法研究了喷动气速和流化气速对喷动-流化床内流化特性的影响。Kuipers等人[3]采用双流体的方法模拟了三维流化床提升管，得到了气固两相的流动特点。李乾军等[4]采用双流体模型研究了喷动-流化床的相关流化特性，模拟结果中，床层上部出现清晰的喷泉状结构，床层上下有明显的分层现象，床层两侧有明显的环核结构。唐楠等[5]采用双流体模型研究了不同流化速度对喷动-流化床流化特性的影响。肖睿等[6]采用双流体模型研究了加压导向式喷动流化床，研究发现颗粒由于受到压力影响在喷动区加速上升，环形区域的气体速度在卷吸颗粒时变大，而空隙率则有下降趋势。Mathur[7]以及唐凤翔等[8]研究了喷动床内的最小喷动速度，其研究表明，最小喷动速度与床层高度成正比，与床体直径成反比。

考虑到研究对象的特性，以及气固两相之间的相互作用力，本文采用欧拉双流体模型，通过颗粒动力学和摩擦应力模型建立稠密气-固两相模拟的本构方程，以研究不同喷动速度、流化速度对喷动-流化床内流动结构、流速以及颗粒脉动的影响。

1 数值计算模型

1.1 控制方程

质量方程，对于气相

(1)

对于固相

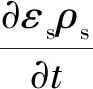
(2)

动量守恒方程，对于气相

(3)

对于固相

(4)

1.2 相间相互作用

本文采用Gidspow[9]曳力模型，它结合了Wen &Yu[10]和Ergun[11]模型各自的优点，其表达式如下所示

(5)

(6)

其中，单颗粒曳力系数Cd取决于颗粒Re数

(7)

(8)

1.3 应力模型

为了封闭固相动量方程(方程(4))，需要给出固相压力ps和应力τs的表达式。根据Johnson & Jackson[12]的研究，固相压力ps和应力τs都由运动-碰撞和摩擦两部分构成

ps=pkc+pf

(9)

τs=τkc+τf

(10)

运动-碰撞部分的固相应力张量为

(11)

式中μb——体积粘度;

μkc——剪切粘度。

摩擦部分的固相应力张量为

τf=2μfDs

(12)

式中μf——摩擦粘度;

Ds——应变张量的偏量。

(13)

气相动量方程(方程(3))中的气相应力张量为

(14)

其中，气相应变量为

(15)

1.3.1 颗粒动理学

运动-碰撞部分的固相压力pkc与固相粘度μkc通常由颗粒动理学[13]进行封闭

pkc=[1+2εs(1+e)g0]ρsεsθ

(16)

(17)

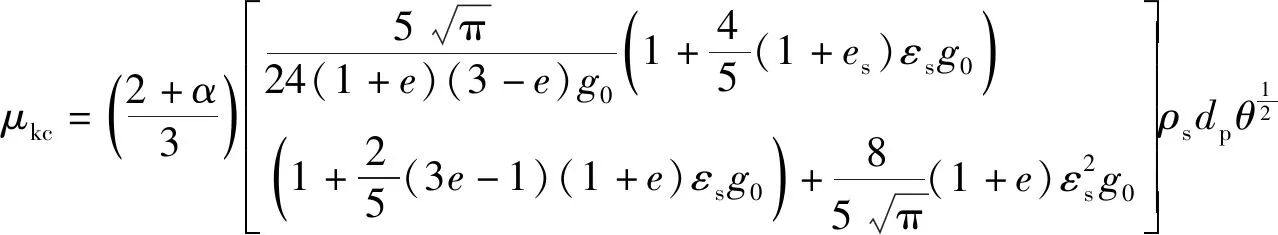
(18)

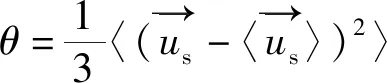
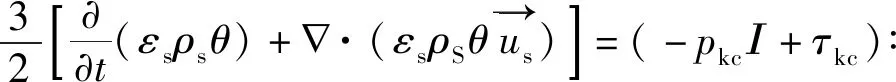
(19)

其中，γs为碰撞耗散

(20)

κs为湍动能扩散率

(21)

本文采用Bagnold[14]的径向分布函数

(22)

1.3.2 摩擦应力模型

在固相高浓度区域，颗粒之间的相互作用不再是瞬时碰撞，而是长时间的摩擦。因此，采用颗粒动理学来封闭固相应力明显不合适，需要引入摩擦应力模型[15]来描述颗粒之间的长时间挤压与摩擦

(23)

(24)

式中φ——内摩擦角。

2 计算条件

2.1 模型结构及边界条件

图 1为本文所模拟的喷动-流化床结构示意图，单位为mm。喷口尺寸为22 mm×12 mm，喷动气流由此喷入流化床内部，底部周围区域为流化风入口，通过调节喷动风速度和流化风速度可以获得不同的流动工况，图1所示的结构尺寸单位均为mm。顶部为压力出口，与大气压力相等。其余部分设为壁面，其中气体为无滑移壁面边界条件，颗粒为部分滑移壁面边界条件。

图1 模型结构示意图

网格尺寸为颗粒尺寸的2倍。初始床层高度为0.228 m，其他模拟参数详见表1。

表1 模拟参数

本文的模拟结果要与Link等人[1]的实验结果进行对比，因此工况的选取与Link等人[1]一致，包含了5种流动结构，具体参数见表2。

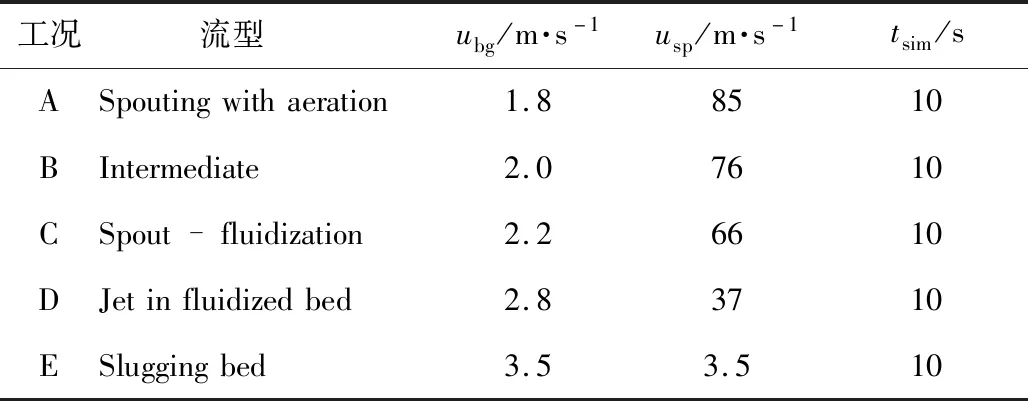
表2 工况参数

注：ubg为流化风速度，usp喷动风速度。

3 计算结果及分析

3.1 流动结构对比分析

(1)工况A：ubg=1.8 m/s；usp=85 m/s

此条件下的流型为Spouting with aeration，数值模拟颗粒浓度云图和Link 等[1]实验快照对比如图2所示。从图中可以看出，在床内中部存在明显的气体通道，气体通道会穿透整个床层。由于喷动风速度远远大于两侧流化风速度，大部分颗粒堆积在床内两侧，只有气体通道中及其附近的颗粒才被流化，随着喷口气体的喷出而呈喷泉状运动，属于典型的喷动流化运动模式。

图2 工况A颗粒浓度云图与实验快照对比

(2)工况B：ubg=2.0 m/s；usp=76 m/s

此条件下的流型为Intermediate，与工况一相比，喷动风速度与流化风速度的比值由47.22降至38。数值模拟颗粒浓度云图和Link等[1]实验快照对比见图3。从图中可以看出，虽然降低了喷动风速度，但在床内中部仍然存在明显的气体通道，空隙率较大。由颗粒速度矢量图可以看出，床内颗粒速度较大的位置在颗粒气体通道内及其周围，且颗粒主要向上运动，而在两侧处颗粒有较小的向下运动趋势，在底部流向气体喷道，形成对称性较好的循环运动。

图3 工况B颗粒浓度云图与实验快照对比

(3)工况C：ubg=2.2 m/s；usp=66 m/s

此条件下的流型为Spout-fluidization，喷动风速度与流化风速度的比值降至30，此时床层上部的颗粒被流化并开始缓慢移动。数值模拟颗粒浓度云图和Link等[1]实验快照对比见图4。由图4可以看出，在床层表面下方气体喷道中可以观察到两侧颗粒形成颈部结构。可能是由于大量颗粒流化喷射后，自由下落至环状回流区对喷道产生挤压作用，造成颗粒周期性地阻塞气体通道。

图4 工况C颗粒浓度云图与实验快照对比

(4)工况D：ubg=2.8 m/s；usp=37 m/s

此条件下的流型为Jet in fluidized bed；Link等实验快照见5(a)，数值模拟颗粒浓度云图见图5(b)。从图中可以看出，这时几乎所有颗粒都在运动，而且在喷口两侧的环状区域中连续形成气泡。气泡在床层底部产生，随着高度增加逐渐长大，上升至一定高度，气泡破裂颗粒先被扬起，然后在重力的作用下自由下落，气固混合运动较为剧烈。但此时，气泡尺寸较小，其形成和传播的时间较短。这种流动结构类似于鼓泡床中的流化特性。但此时仍然还存在一个气体通道，该通道周期性地被大量的颗粒阻塞，且通常发生在床层的低位。

图5(a) 工况D,Link等实验快照图[1]

图5(b) 工况D数值模拟颗粒浓度云图

(5)工况E：ubg=3.5 m/s；usp=3.5 m/s

此条件下的流型为Slugging bed，此时所有颗粒都在运动并形成了不均匀结构-颗粒聚团。图6展示了颗粒聚团形成的不同阶段， Link 等的实验快照见图6(a)，本文数值模拟颗粒浓度云图见图6(b)。从图中可以看出，颗粒形成聚团并周期性的向上运动，然后在重力作用下下落，数值模拟结果与实验结果吻合。除了颗粒聚团之外，在床层底部还形成了较小的气泡，沿着床层高度逐渐长大，上升至自由表面后发生破裂。

图6(a) 工况E,Link等实验快照图[1]

图6(b) 工况E数值模拟颗粒浓度云图

3.2 流动参数分析

3.2.1 颗粒速度分布

图7表示在0.05 m、0.1 m、0.15 m和0.2 m高度处，不同工况下颗粒的径向速度分量。在0.15 m以上的区域，工况A至工况D的颗粒由喷口向两侧喷出，下落并回流至环状区，这一区域颗粒不再继续大幅度上升，而是向两侧扩散，属于喷泉区。在0.1 m以下区域，从喷泉区落下的颗粒进入环状回流区，由于喷口处的颗粒被喷动风带走，环状区域的颗粒会流向喷口形成循环。环状回流区的颗粒径向速度刚好与喷泉区相反。工况E的径向速度均为正值，说明颗粒是形成聚团整体移动。

图7 不同高度处的颗粒径向速度分量

图8表示在0.05 m、0.1 m、0.15 m和0.2 m高度处，不同工况的颗粒轴向速度分量。如图所示，工况A至工况D的轴向速度曲线在中轴处存在一个波峰。速度的最大值与观察高度成反比，这是因为观察高度越高，喷动风的速度衰减得越多，且颗粒自身重力作用也会使颗粒速度减小。由喷口往外颗粒轴向速度逐渐减小，在靠近壁面处为负值，这是因为壁面附近的颗粒在回落颗粒的挤压下而向下运动。曲线关于中轴对称分布两个波谷，这是因为四周环空区下落的颗粒在壁面处由于壁面的摩擦作用，速度会有所减小，下降速度的最大值大约在离壁面0.02 m的位置。

图8 不同高度处的颗粒轴向速度分量

工况E条件下，轴向速度曲线较平缓没有十分陡峭的波峰波谷，这是因为颗粒聚团整体运动，在y轴方向有相近的速度。

3.2.2 颗粒拟温度分布

颗粒拟温度用来表征颗粒脉动能，数值越大表明颗粒脉动越剧烈。图9表示在0.05 m、0.1 m、0.15 m和0.2 m高度处，不同工况下的颗粒拟温度的分布曲线。如图所示，在0.1 m以下区域，工况A至工况D颗粒拟温度曲线均在中轴处出现一个陡峭的波峰，远离喷口中心的颗粒拟温度较低，趋近于0。这是因为中心处为喷口，高速射流的喷动风夹带着颗粒剧烈运动，因此脉动剧烈。四周的流化风速度较低，不会使颗粒发生剧烈脉动。此区域工况E的颗粒拟温度曲线十分平缓且接近于0，说明该条件下，这一区域的颗粒脉动都十分微弱。

图9 不同高度处颗粒拟温度分布

在0.15 m以上的区域，工况A至工况D颗粒拟温度曲线在中轴处仍存在一个波峰。与0.1 m以下区域相比，波峰的最大值由原来的0.3减小到0.17 m2/s2左右；且波峰的径向跨度变宽；靠近壁面处的颗粒拟温度升高，使得曲线出现了两个波谷。这是因为越往上，喷动风速度衰减越多，颗粒的脉动强度也随之降低；喷动区上升的颗粒至一定高度后回落，与下方上升的颗粒、气流以及壁面发生碰撞，使得颗粒的湍动加剧。工况E的颗粒拟温度沿径向仍较平缓，曲线的中间段仍趋近于0，只是在靠近壁面处略有上升，有可能是气流沿壁面上升穿过颗粒聚团导致的。

4 结论

本文采用Euler-Euler双流体模型，建立了布风板为平板型的喷动流化床计算模型，对喷动流化床内气固两相流动进行了数值模拟计算，调节流化风速度和喷动风速度模拟计算了5个工况，分别对应于喷动流化床的5种流型，得到了床内颗粒速度、浓度以及颗粒拟温度等参数分布。

模拟得出的颗粒浓度分布与J.M.Link等[1]的实验快照对比效果理想，清晰直观的反映出喷动流化床浓度分布规律；尤其对于Spout-fluidization流型在喷道中部会形成颈部结构，以及Slugging bed流型会形成不均匀结构——颗粒聚团，模拟计算浓度云图能够清晰观察到这些结构。

在喷射区，颗粒主要沿竖直方向向上运动，速度的最大值与喷动风速度成正比；在喷泉区，颗粒主要沿水平方向向壁面扩散，而竖直方向的速度已大幅降低；在环隙区，颗粒在重力及喷动风影响下沿竖直方向下运动，但下降速度并不大，且在壁面附近由于壁面摩擦作用，会出现速度降低的“壁面效应”。

在喷动流化床的低位，喷射区的颗粒拟温度最高，颗粒拟温度的最大值也与喷动风速度成正比，在环隙区颗粒拟温度几乎等于0；在喷动流化床的高位，喷泉区中心的颗粒温度较高，但是远小于喷动区中心的颗粒拟温度，与喷动流化床低位的环隙区不同，喷泉区的壁面附近颗粒拟温度略有回升，这是向四周扩散的回落颗粒速度脉动引起的。

符号表

拉丁字母

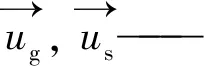
t——时间

pg,ps——气相，固相压力

Cd——单颗粒曳力系数

dp——颗粒直径

Re——颗粒雷诺数

pkc——运动-碰撞颗粒压力

Ds——固相应变张量的偏量

Dg——气相应变张量

I——单位张量

e——恢复系数

g0——径向分布函数

ks——固相湍动能扩散率

pf——固相摩擦压力

希腊字母

ρg,ρs——气相，固相密度

εg,εs——气相，固相浓度

εs,max——填充极限

τg,τs——气相，固相应力张量

τkc——固相运动-碰撞应力

τf——固相摩擦应力

μb——固相体积粘度

μkc——固相运动-碰撞粘度

μf——固相摩擦粘度

β——曳力系数

φ——内摩擦角

θ——颗粒拟温度

γs——湍动能碰撞耗散率