洛阳地区砂卵石地层渗透系数与有效粒径关系

李 达, 高笑娟, 马建军, 雷居强

(河南科技大学 土木工程学院，河南 洛阳 471023)

0 引言

洛阳市轨道交通1号线全长22.35 km，其东段的青年宫至杨湾等5个车站基坑底部位于第四系冲积、洪积松散～稍密的砂卵石潜水含水地层中。地区经验显示该地层渗透系数为100～150 m/d，原有的经验取值范围太大，不能有效指导轨道交通1号线深基坑工程建设[1-2]。

砂卵石地层是典型的自然产物，其渗透系数具有明显的不均匀性和地域性。而且渗透系数的影响因素较多，如土的粒径级配、孔隙比、结构和矿物成分等，其中，粒径级配和孔隙比对土的渗透系数影响较大。就粗颗粒土而言，其渗透系数计算经验公式已有大量研究。文献[3]在对渭河粗粒土进行渗透系数规律性试验后，得出了渗透系数与限制粒径(d30)、有效粒径(d10)和控制粒径(d60)相关的结论，并修正了太沙基(Terzaghi)渗透系数计算公式。文献[4-5]利用测得的砂卵石的有效粒径d10、控制粒径d60、不均匀系数(Cu)和曲率系数(Cc)等指标，通过数学拟合得到了渗透系数预测的多元线性回归模型。文献[6]探讨了砂土有效粒径、孔隙率和不均匀系数对渗透系数的影响，得出估算天然砂土渗透系数的经验公式。文献[7]建立了渗透系数与特征粒径指标之间的二次多项式关系模型。文献[8]证明了金沙江流域的级配河砂渗透系数与平均粒径间成正相关。文献[9]研究表明：渗透系数随颗粒级配特征值d20和曲率系数的增大而增大，随干密度和颗粒球形度的增大而减小。对于碎石土材料，文献[10]的研究表明：由全级配预测渗透系数较精确，经验公式存在适用局限性。文献[11]进行了不同级配下的粗颗粒土渗透试验，表明各粒径颗粒含量均对渗透系数有影响。文献[12-13]采用遗传算法和反向传播(back propagation，BP)算法，用神经网络分析和预测粗粒土的渗透系数，发现各级配粒径均对渗透系数有影响。

综上所述，不同地区和不同土层的渗透系数计算公式各不相同，但粗颗粒土渗透系数与土的特征粒径和孔隙比等参数直接相关。已有研究多针对砂土进行，而关于砂卵石渗透系数计算经验公式的研究相对较少。然而，由于砂卵石地层的沉积状态不同，其特征粒径和孔隙比具有强烈的区域性。因此，为更好地服务于洛阳地区的轨道交通等地下工程建设，有必要根据当地实测资料对其砂卵石潜水含水层的渗透系数计算公式进行研究，提出并修正适用于洛阳地区砂卵石地层的渗透系数计算经验公式。

1 砂卵石地层渗透性和颗粒特征

基于200余份各类工程的岩土工程勘察报告，调研了洛阳地区砂卵石地层渗透系数取值现状。经统计分析，得到了轨道交通1号线沿线各种砂卵石地层的渗透系数变化范围和建议取值，如表1所示。由表1可知：洛阳地区广泛分布的砂卵石(Q3al+pl)和砂卵石(Q4al+pl)地层的渗透系数值和变化范围均很大。然而渗透系数变化区间过大，不利于准确估算基坑的涌水量，将对深基坑降水设计和施工造成不利影响。

表1 轨道交通1号线沿线砂卵石地层渗透系数调研统计表

为揭示洛阳轨道交通1号线相关站点的砂卵石地层颗粒特征，在各车站基坑土方开挖过程中，对丽景门站、启明南路站、应天门站、杨湾站、塔湾站等砂卵石地层深厚的车站进行开挖面取土。利用现场土样，对不同地层的砂卵石颗粒进行筛分试验，得到颗粒级配和特征粒径[14]。

1.1 地层沉积形态

启明南路站及其以东的各车站基坑均位于洛河Ⅰ级阶地，上更新统冲洪积层中密～密实(③9-3(Q3al+pl))砂卵石地层连续分布。③9-3砂卵石地层在启明南路至杨湾站的埋深为10～13 m，层厚13～17 m，其上覆盖有松散的上更新统冲洪积(②9-2(Q3al+pl))砂卵石地层。由于水力分选沉积条件不同，各车站基坑不同埋深地层的卵石颗粒特征和颗粒间填充物均有显著区别。以丽景门站和杨湾站为例，图1给出了两车站③9-3砂卵石地层特征。如图1所示，筛分后两站点的土样有明显区别。对比图1a和图1b所示的颗粒间填充物可知：丽景门站土样含有部分黏土颗粒，而杨湾站土样的填充物多为细砂。

(a) 丽景门站③9-3砂卵石筛分后土样(b) 杨湾站③9-3砂卵石筛分后土样

1.2 粒径级配曲线

对各车站所取土样进行筛分，可以得到特征粒径和级配曲线。仍以丽景门站和杨湾站为例，图2给出了两车站③9-3砂卵石土样的颗粒级配曲线。相应地，可以得到丽景门站砂卵石土样的不均匀系数Cu=69.1，曲率系数Cc=12.94；杨湾站砂卵石土样的不均匀系数Cu=140.28，曲率系数Cc=19.48。如图2所示，两站点砂卵石地层土样的颗粒级配曲线均不光滑，有明显拐点。同时由Cu和Cc值可知，砂卵石地层土样级配不良。由图2a可知：粒径级配曲线存在明显的平台段。d30和d10之间粒径存在颗粒缺失，砂卵石土可判定为管涌型土。对比图2a和图2b可知：杨湾站砂卵石地层的填充颗粒缺失更明显，可以判断其渗透系数更大。

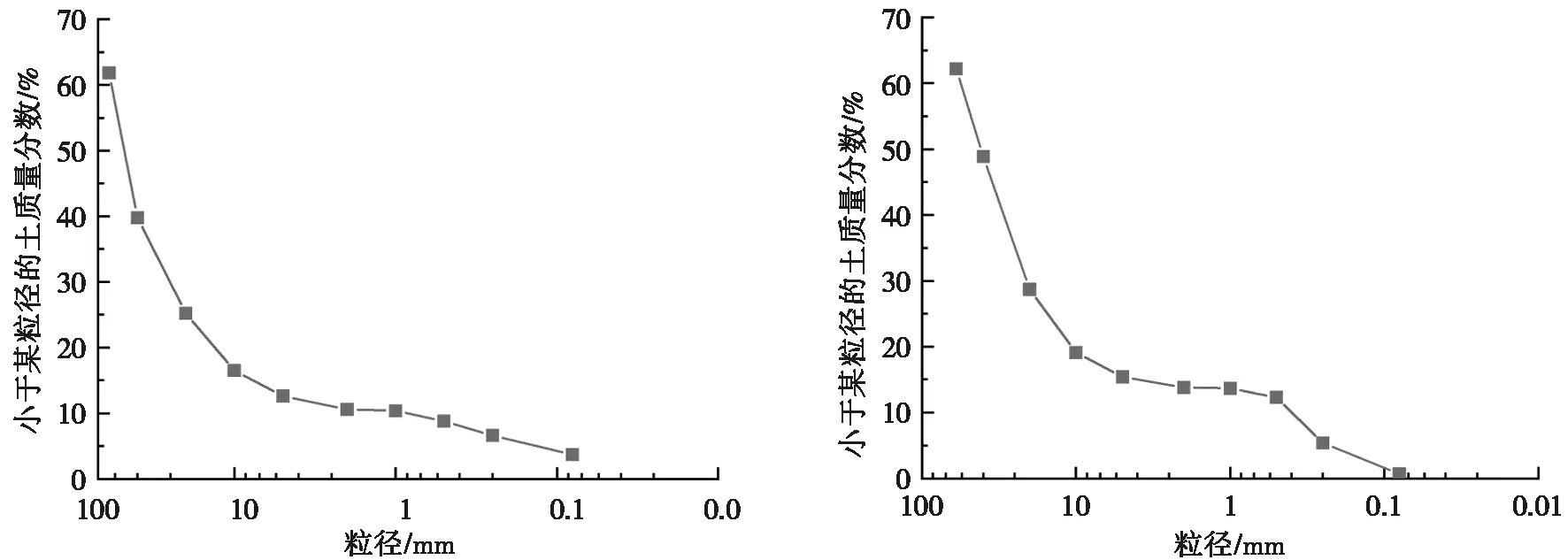
(a) 丽景门站土样粒径级配曲线 (b) 杨湾站土样粒径级配曲线

2 渗透系数与有效粒径的关系

由无黏性土渗透系数计算经验公式可知，土层的特征粒径和孔隙比与渗透系数有直接关系[5-7]。利用已有的经验公式，计算可得砂卵石潜水含水层的渗透系数。然而经验公式具有明显的局限性，需要结合洛阳地区砂卵石地层的颗粒特征进行修正。

2.1 开挖面取土所得d10与k的关系

有效粒径d10对渗透系数k有明显的影响，k值随d10的增大而增大。由文献[1,15-16]可知：有效粒径d10多以平方的形式出现在渗透系数计算的经验公式中：

k=2d102e2；

(1)

k=cd102；

(2)

k=c×d102(0.7+0.03t)，

(3)

其中：e为孔隙比；c为无量纲经验因数；t为测试时土层的温度,°C。

由于砂卵石的孔隙比缺少可参考数据，本文根据勘察报告中的超重型圆锥动力触探试验N120锤击数和对土层密实程度的经验判断，呈稍密状态的②9-2砂卵石取e=0.41，中密状态的③9-3砂卵石取e=0.39。进而，分别利用式(1)～式(3)初步估算砂卵石地层的渗透系数。表2给出了利用经验公式估算的不同车站砂卵石地层的渗透系数值，并与现场抽水试验所得渗透系数对比，其中，式(2)中取c=100，式(3)中取c=700，t=20 °C。

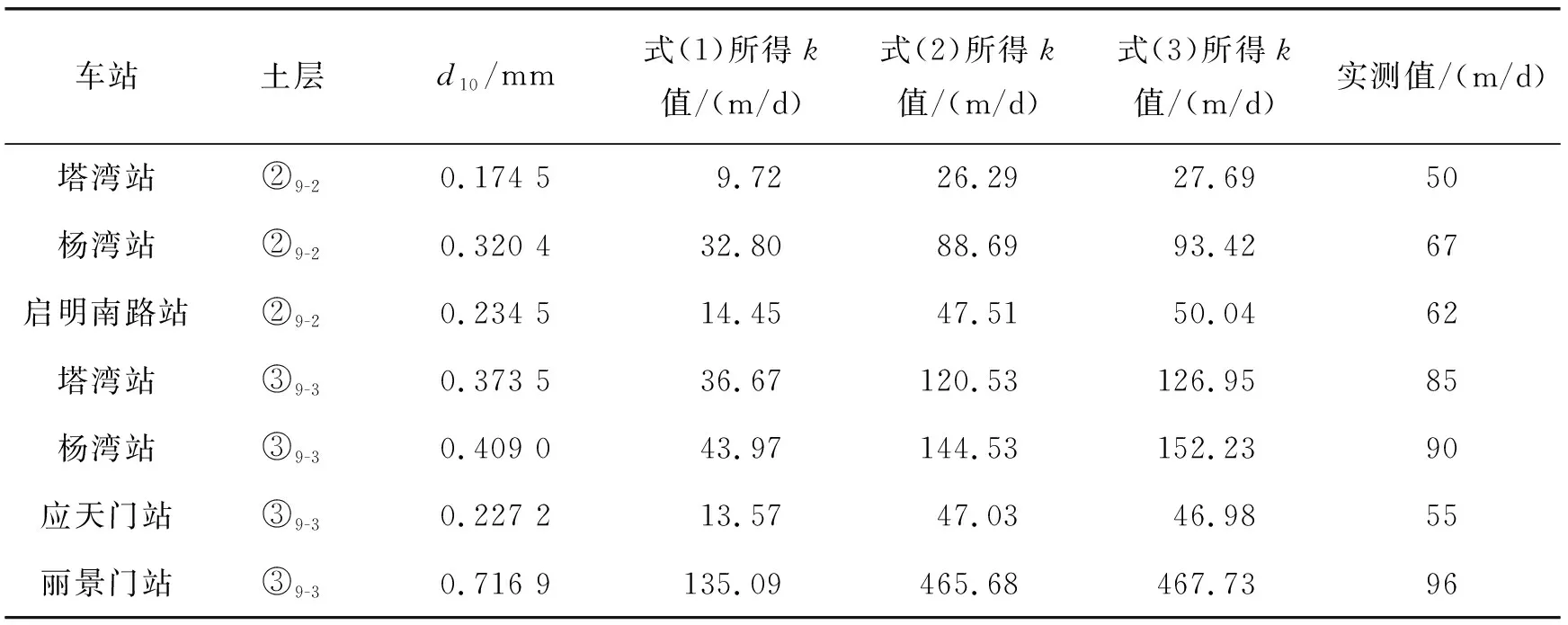
表2 经验公式估算的不同车站砂卵石地层渗透系数k值

由表2可知：3个经验公式计算所得的砂卵石地层渗透系数与实测值偏差较大。当d10< 0.2 mm时，计算值远小于实测值，式(1)所得k值约为实测值的1/6；式(2)和式(3)所得k值相近，约为实测值的1/2。当d10> 0.7 mm时，计算值远大于实测值，式(1)所得k值超过实测值1.5倍；式(2)和式(3)所得k值接近实测值的5倍。总体而言，式(1)所得k值与实测值之间偏差较大。在d10< 0.3 mm时，式(2)和式(3)所得k值的偏差较小。由此可知，适用于砂土层渗透系数计算的经验公式并不适用于洛阳地区的砂卵石土层。因此，需要结合洛阳地区②9-2和③9-3层砂卵石的颗粒特征修正渗透系数和有效粒径之间的关系。

为便于应用，基于太沙基渗透系数计算经验公式(1)，假定k1为与砂卵石地层的有效粒径d10和孔隙比e直接相关的名义渗透系数，其表达式为式(4)。实测渗透系数k与k1之间存在函数关系，由式(5)表示：

图3 渗透系数实测值和拟合曲线

(4)

k=f(k1)。

(5)

假定f(k1)为指数函数，经数值拟合可得较好的相关性，相关系数达0.893 71。图3给出了渗透系数实测值和拟合曲线。相应地，可以得到拟合曲线表达式：

(6)

利用式(6)，可估算有效粒径d10为0.2～0.7 mm砂卵石地层的渗透系数。表3给出了砂卵石地层渗透系数的计算值与实测值的偏差。如表3所示，对于同一车站和地层，每一组数据偏差平均值均在15%以内。

表3 利用拟合公式对筛分试样计算的k值表

2.2 勘探孔取土的d10与k的关系

由于砂卵石地层的土体颗粒直径差距大，工程勘察时探孔取土和现场开挖面取土所得数据之间存在差别。特别是卵石粒径较大时，两种方法测得的特征粒径差别较大。将丽景门站等站点工程详勘报告中的有效粒径d10代入式(4)，进而利用式(6)求得砂卵石地层的渗透系数k。表4列出了利用勘探孔取土所得数据计算的k值，为减小误差，计算时剔除了d10的最大值和最小值。

由表4可知：因开挖面取土和勘探孔取土方式不同，筛分所得的特征粒径不同，因而利用式(6)计算k值与实测值间有较大差别。就丽景门站而言，勘探孔取土所得颗粒粒径大，d10值超出了式(6)的适用范围。显然此时式(6)中第1项约为0，则仅剩常数项，因此，此时求得的k值虽然与实测值差别小，但不具通用性。应天门站勘察所得的d10平均值为1.08 mm，远大于开挖面取土所得值，求得的k值约为实测值的1.5倍。塔湾站和杨湾站勘察所得d10值与开挖面取土所得值差别不大，因此渗透系数计算值和实测值的偏差相对较小。

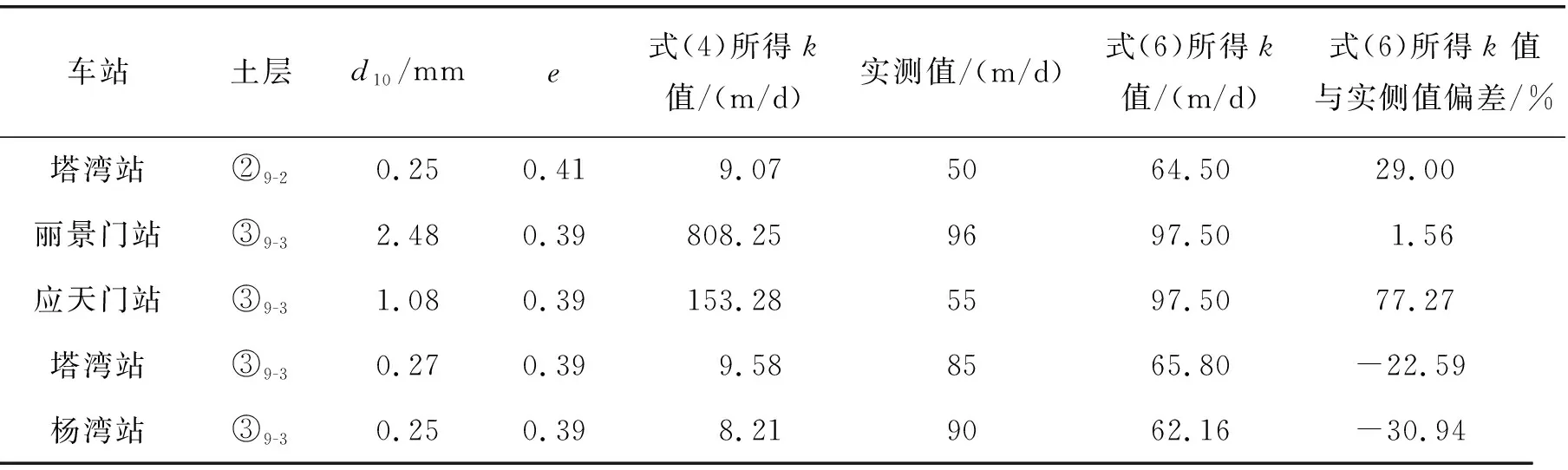
表4 根据现场工程勘察数据计算的k值表

总体而言，砂土颗粒(粒径为0.075～2 mm)占比对开挖面取土和勘探孔取土所得特征粒径的差别有显著影响。若砂土颗粒含量大，两种方法所得结果的差别则较小。因此，此时可以考虑将曲率系数Cc引入式(4)，假定其用式(7)表示砂卵石地层的名义渗透系数k2:

(7)

利用勘探孔取土所测得的数据代入式(7)，进而利用式(6)可得砂卵石地层的渗透系数k。表5给出了考虑土样曲率系数时求得的砂卵石地层渗透系数值。由表5可知：考虑曲率系数的影响时，式(6)所得渗透系数计算值与实测值之间的偏差显著减小。同时由应天门站渗透系数计算结果可知：由于勘探孔取土造成砂卵石土样中细颗粒缺失，可能导致利用经验公式(7)估算的渗透系数值偏大。

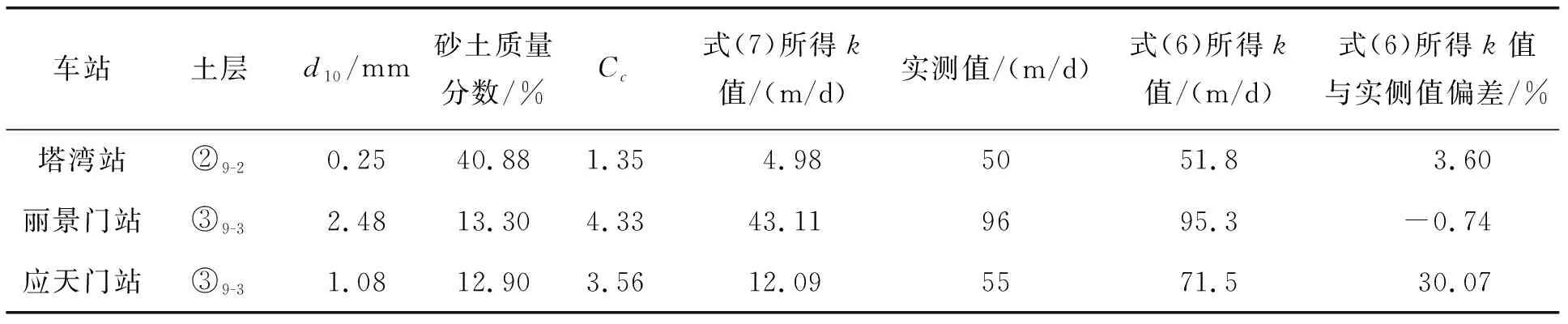
表5 考虑Cc时得到的k值

3 结论

(1)基于太沙基的渗透系数计算经验公式，利用开挖面取土筛分所得数据，可得适用于洛阳地区砂卵石地层渗透系数的计算公式。

(2)若利用勘探孔取土所测的土工参数，则需考虑现场取样引起的细颗粒缺失，因此，应将粒径级配累计曲线的曲率系数引入砂卵石地层渗透系数计算的经验公式。