轮边驱动式电动拖拉机转向特性分析

韩 冰，刘孟楠，徐立友

(1. 河南科技大学 车辆与交通工程学院，河南 洛阳 471003；2. 西安理工大学 机械与精密仪器工程学院，陕西 西安 710048)

0 引言

电动拖拉机具有零排放、低噪声、高效率和牵引性能好等特点[1-2]，其传动系统采用电力驱动，可极大简化整机结构[3]。轮边驱动式电动拖拉机取消了半轴、万向节、差速器、变速器等传动部件，由电机通过减速器直接与各个驱动轮相连[4]，其驱动系统集成度高、响应快且控制更灵活[5]。但轮边驱动式电动拖拉机在高速或松软路面行驶转向时，轮胎容易出现滑转、失稳等问题[6-7]。

针对车辆差速转向存在的问题，国内外学者进行了相关研究。文献[8]通过分析汽车动力学模型及电动轮差速转向的原理，提出了用神经网络的方法控制差速系统。文献[9]在检验了制动转向系统的有用性以后，认为该系统具有使用差速制动力进行转向干预的可行性。文献[10]分析了三自由度的差速转向车辆动力学模型，对电动轮汽车差速转向系统参数进行了集成优化设计。文献[11]分析了差动转向车辆的动力学特性，为轮边电机驱动差动转向车辆设计了纵侧向解耦的动力学控制器。上述文献对轮式车辆差速转向的研究多集中在汽车领域，而与拖拉机相关的研究较少，且并未考虑转向系统性能在差速率变化下的影响。

考虑到拖拉机整车结构、车速、转向半径等参数的要求均与汽车不同[12]，且差速率的取值对电动拖拉机差速转向系统至关重要，故本文对差速率变化下的轮边驱动式电动拖拉机的转向特性开展了相关研究。以额定功率132 kW的轮边驱动式电动拖拉机为工程实例，建立满足稳态转向特性的运动学模型、三自由度(3 degree of freeodom，)动力学模型、滑转率-车速求解模型和转向轨迹数学模型，分析差速率变化对电动拖拉机稳态转向特性的影响。

1 轮边驱动式电动拖拉机的转向问题

选取轮边驱动式电动拖拉机为研究对象，其底盘采用四轮独立驱动，无机械差速器。轮边驱动式电动拖拉机的结构如图1所示，由车轮、制动器、控制器、动力电池及轮边电机等构成。拖拉机驱动方式为四轮驱动，主控制器负责采集传感器信号和发送控制指令；动力电池为整车提供能量；轮边电机通过减速器及传动轴将动力传递给车轮。

图1 轮边驱动式电动拖拉机的结构

由于轮边驱动式电动拖拉机没有转向机构和前轮转角，需要靠两侧车轮的轮速差和转矩差完成差速转向。当轮边驱动式电动拖拉机转向时，传感器把采集到的驾驶员转向信号传输给主控制器，由主控制器计算当前转角对应的差速率，控制轮边电动机的转速和转矩，完成拖拉机的差速转向。考虑到拖拉机的作业工况复杂多变，而不同工况对应的差速率对拖拉机转向特性的影响也不同，故需要根据实例展开仿真分析。

差速率也即轮边驱动式电动拖拉机两侧车轮的差速程度。当拖拉机右转时，差速率e计算式[12]为：

(1)

其中：V1为拖拉机左侧瞬时轮速，m/s；V2为拖拉机右侧瞬时轮速，m/s，V为拖拉机质心瞬时轮速，m/s。

根据拖拉机差速率与当前车速，可获得内外侧车轮的期望轮速，转向时期望轮速的计算式[13]为：

Vq1=u(100+e)/100；

(2)

Vq2=u(100-e)/100，

(3)

其中：u为车速，m/s；Vq1为拖拉机外侧轮速，m/s；Vq2为拖拉机内侧轮速，m/s。

2 轮边驱动式电动拖拉机转向模型

2.1 运动学模型

轮边驱动式电动拖拉机转向过程中，在转向梯形的约束下，前后轴应该有同一个转向中心，并且绕着各自的圆周做纯滚动[14-15]。

假设在某时刻，拖拉机以瞬时转向半径R绕瞬时圆心点O转向，其车速及半径关系[16]如下：

(4)

(5)

(6)

(a) 模型俯视图(b) 模型侧视图图2 3DOF转向动力学模型

其中：B为两侧主销轴线与地面交点之间的中心距离，m；△V为两侧驱动轮轮速之差，m/s。

2.2 三自由度(3DOF)动力学模型

轮边驱动式电动拖拉机在行驶过程中，横摆运动与侧倾运动相互影响，故3DOF动力学模型更符合轮边驱动式电动拖拉机的实际摆动情况[17]。考虑到轮边驱动式电动拖拉机没有转向机构，需去掉3DOF动力学模型[18]中的前轮转向角，根据经典力学理论及轮胎受力[19]，建立改进后的3DOF转向动力学模型，如图2所示。

轮边驱动式电动拖拉机侧向运动微分方程为：

(7)

轮边驱动式电动拖拉机横摆运动微分方程为：

(8)

轮边驱动式电动拖拉机侧倾运动微分方程为：

(9)

其中：

(10)

其中：m为总质量，kg；mS为载质量，kg；u为沿x轴方向的前进速度，m·s-1；a、b分别为前轴、后轴到质心的距离，m；ωr为横摆角速度，rad·s-1；β为质心侧偏角，rad；k1、k2分别为前轮、后轮侧偏刚度；φ为侧倾角，rad；Ix为绕x轴的转动惯量，kg·m2；Iz为绕z轴的转动惯量，kg·m2；Ixz为绕x轴和z轴的转动惯量，kg·m2；hS为侧倾中心到质心的距离，m；Cφ为侧倾阻尼，N·m/(rad·s-1)；Kφ为侧倾刚度，N/rad；ξf、ξr分别为前轮、后轮侧倾转向因数；Fyi(其中，i=1、2、3、4)为轮胎受到沿y方向的侧偏力，N；Fyf为前轮受到的侧偏力之和，N；Fyr为后轮受到沿侧偏力向的地面反作用力，N；△Fxf为前轮纵向力之差，N；△Fxr为后轮纵向力之差，N。

2.3 滑转率-车速求解模型

轮胎滑移率，即轮胎滑动状态占总状态的比[20]。拖拉机低速直线行驶时发生滑转的可能性较小[21]，而在差速转向过程中，外侧车轮速度增加，内侧车轮速度减小，车轮易发生滑转。外侧和内测滑转率[22]分别为：

(11)

其中：Vs为车轮瞬时速度，m/s；ωs为车轮旋转角速度，rad·s-1；r为车轮转动半径，m；Sy为车轮外侧滑转率，%；Sz为车轮内侧滑转率，%。

当Sy(或Sz)超过30%时，纵向附着系数和横向附着系数都会大幅下降，从而影响到拖拉机运行的稳定性[23]。对于本文的差速转向系统而言，需要保持Sy(或Sz)不超过 30% 。根据3DOF动力学模型，由前后轮侧偏角和速度关系，计算求得左前轮Vf1、右前轮Vf2、左后轮Vr1和右后轮Vr2的车速分别为：

(12)

2.4 转向轨迹模型

本文采用坐标随时间变化的函数关系来对轮边驱动式电动拖拉机的行驶轨迹进行研究，以轮边驱动式电动拖拉机车轮的瞬时速度为输入因子，通过建立拖拉机差速转向轨迹模型，找到拖拉机质心随时间的坐标变化方程[24-25]，并利用MATLAB软件画出拖拉机的运行轨迹图。差速转向轨迹运动模型如图3所示。图3中，p(X,Y)为拖拉机质心的位置，虚线为质心p的运行轨迹。选取质心p为研究对象，假设拖拉机经历了tk到tk+1时间的转向后，其位置变化如图3所示。

图3 差速转向轨迹运动模型

pk和pk+1为质心运动的两个连续位置，xp和xp+1为拖拉机质点的速度方向，当tk到tk+1的时间差足够小时，由图3中的几何关系可以得到：

(13)

其中：Ψp为拖拉机的航向角，rad；σ为拖拉机与x轴方向的夹角，rad；θp为拖拉机的横摆角，rad；Vp为拖拉机质心的速度，m/s；Vpx为拖拉机质心沿x轴方向的速度，m/s；Vpy为拖拉机质心沿y轴方向的速度，m/s。

对瞬时速度积分即可得质心p在t时间内所经过的每个点的横纵坐标，这些点的连线为质心p在t时间内的运行轨迹，p点的初始坐标为(0,0)，则：

(14)

3 轮边驱动式电动拖拉机差速转向特性仿真分析

本文以132 kW轮边驱动式电动拖拉机为研究实例，当拖拉机运输作业时，依据装载质量和车速，将仿真工况划分为重载低速工况和轻载高速工况。仿真时可假设拖拉机行驶速度和转向系统传动比都恒定。当拖拉机以恒定速度直线行驶时，驾驶员给拖拉机一个差速率输入，根据差速率在运动学模型中计算建立横摆角速度输入信号时间序列，根据3DOF动力学模型、滑转率-车速求解模型和转向轨迹模型求解仿真。其中，驾驶员输入模型、运动学模型、3DOF动力学模型、转向轨迹模型和滑转率-车速求解模型，构成轮边驱动式电动拖拉机差速转向系统仿真模型，如图4所示。

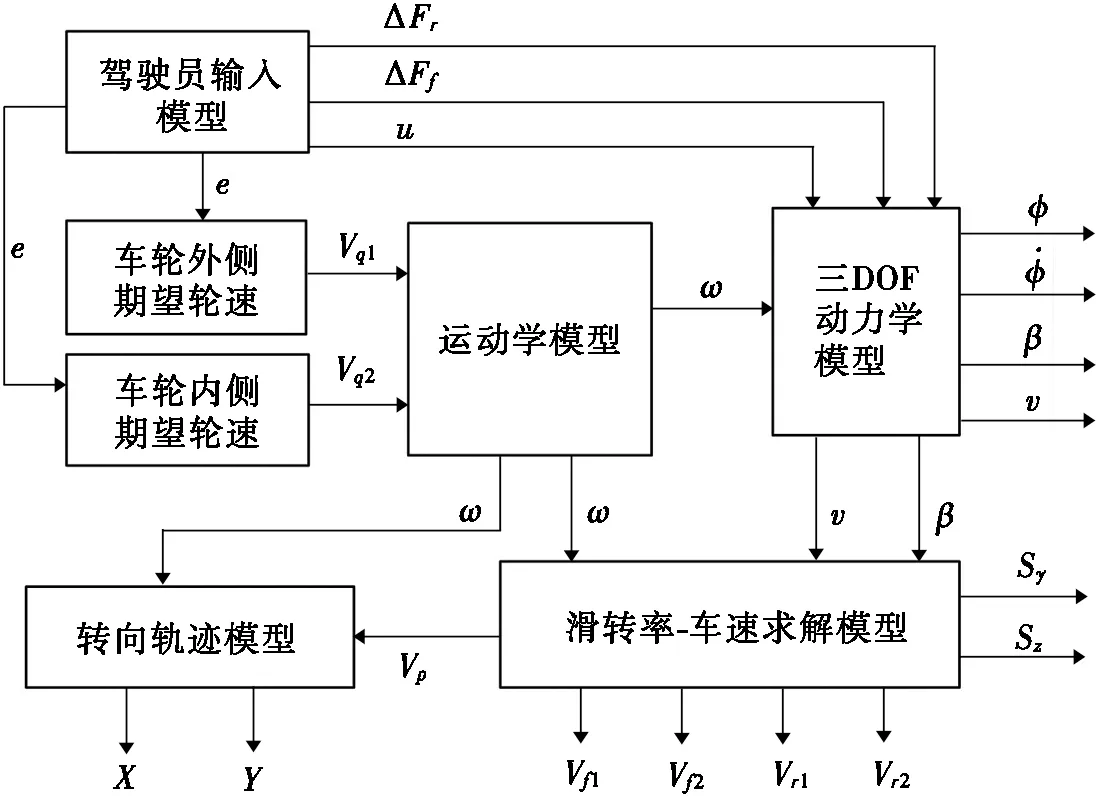
图4 系统仿真模型结构图

在上述模型的基础上，在MATLAB软件中对轮边驱动式电动拖拉机转向系统进行仿真试验。其中，仿真采用的轮边驱动式电动拖拉机模型参数如表1所示。

表1 轮边驱动式电动拖拉机模型参数

3.1 重载低速工况转向特性

轮边驱动式电动拖拉机在重载低速工况行驶时，为提高作业效率，转弯半径通常较小，故差速率的取值偏大。为模拟拖拉机重载低速工况的转弯状态，ms取值为25 t，m取值为26.15 t，u的取值为5 km/h，e取值分别为5、10和20，仿真时间取值为18 s，可得到对应的横摆角速度曲线、侧倾角响应曲线、速度-滑转率曲线。在其他条件不变的情况下，将仿真时间取20 s，可得到拖拉机在重载低速条件下的转向轨迹曲线。

图5为重载低速工况的横摆角速度曲线。如图5所示，运动学模型求解的稳态横摆角速度随着差速率的增大也逐渐增大，且横摆角速度的稳态值越大，拖拉机转弯半径越小，转向更灵活。图6为拖拉机在重载低速工况下的侧倾角仿真曲线，拖拉机转弯时差速率越大，则稳态时的侧倾角越大，超调量越小，故拖拉机行驶时转弯的稳定性变差。仿真得到的侧倾角最大值为1.72°，远小于拖拉机安全行驶的最大侧倾角，可满足拖拉机转弯行驶对侧倾角的要求。

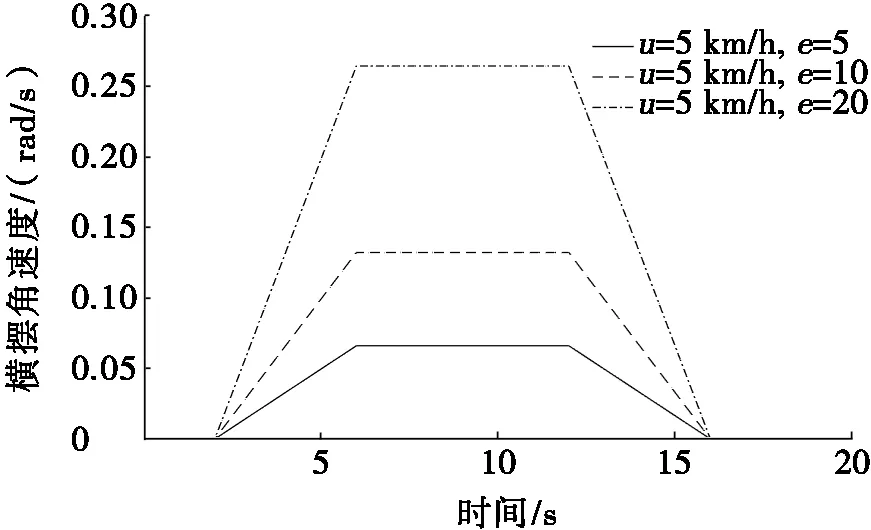
图7 重载低速工况的转向轨迹仿真曲线

图7为轮边驱动式电动拖拉机在重载低速工况下的转向轨迹仿真曲线。由图7可知：在同样的车速下，随着差速率增大，转弯半径变小，对应转过的距离相对较小，有利于提高拖拉机的转向性能，且轨迹模型验证了差速转向模型的可行性。

图8a为e=5、10和20时的车速仿真曲线；图8b为e=5、10和20时，车轮内、外侧的滑转率仿真曲线。由图8可知：随着差速率的增加，横摆角速度随之增大，对应的车速差逐渐增大，且同侧车轮轮速差也逐渐增大；车轮外侧滑移率和内侧滑转率随着差速率增大，滑转率在最大差速状态e=20时仍小于20%，模型满足要求。根据仿真结果可知：当拖拉机在重载低速工况行驶时，滑转率对拖拉机的影响较小，差速率可取较大值，尽可能地缩小转弯半径，达到快速转向的目的。

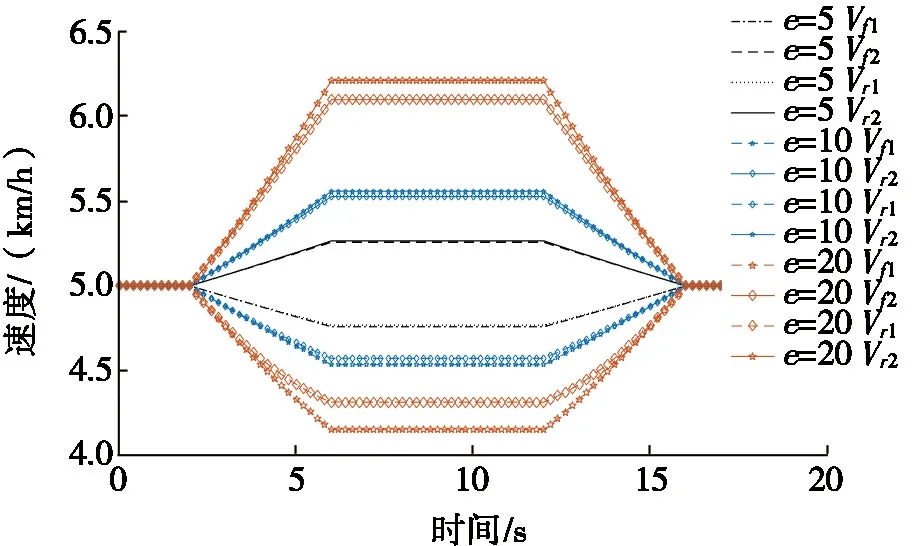
(a) e=5、10和20时速度曲线 (b) e=5、10和20时滑转率曲线

3.2 轻载高速工况转向特性

轮边驱动式电动拖拉机在轻载高速工况行驶时，当转弯幅度大时，拖拉机的稳定性差。因此，差速率通常取值偏小，为模拟拖拉机轻载高速工况的转弯状态，mS取值为5 t，m取值为6.15 t，u的取值为40 km/h，分别输入e为1、3和5，仿真时间取为18 s，可得到横摆角速度、侧倾角响应、速度和滑移率曲线。

图9为拖拉机轻载高速工况的横摆角速度曲线。由图9可知：稳态横摆角速度值随着差速率逐渐增大，且随着横摆角速度的稳态值增大，拖拉机转弯半径则变小。图10为拖拉机轻载高速工况的侧倾角仿真曲线。由图10可知：拖拉机转弯时差速率越大，则稳态时的侧倾角越大，超调量越小，故拖拉机行驶时转弯的稳定性变差。仿真得到的侧倾角稳态最大值为3.44°，大于同等差速率条件下低速行驶拖拉机的最大侧倾角。

图9 轻载高速工况的横摆角速度曲线

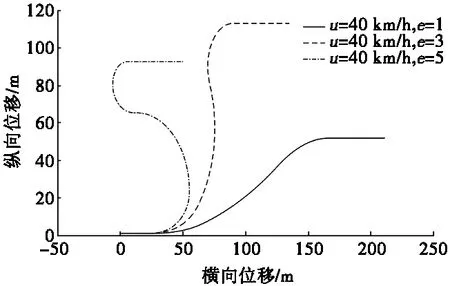
图11 轻载高速工况的转向轨迹曲线

在其他条件不变的情况下，将仿真时间取20 s，可得到拖拉机的转向轨迹曲线，如图11所示。由图11可知：在同样的车速下，随着差速率增大，转弯半径变小，可以转过半径较小的弯道。由轨迹曲线仿真结果可知：轻载高速工况下拖拉机的行驶轨迹对差速率的变化更敏感，差速率细微的变化便可改变拖拉机的行驶轨迹。

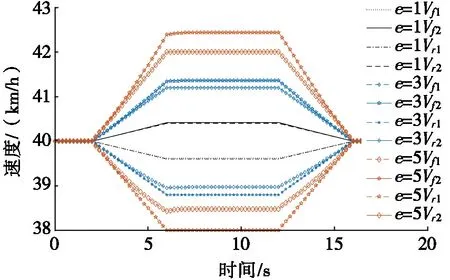
图12a为e=1、3和5时车速仿真曲线；图12b为e=1、3和5时，车轮内、外侧的滑转率仿真曲线。由图12可知：随着差速率的增加，车轮的车速差逐渐增大；车轮外侧滑移率和内侧滑转率随着e增大，稳态滑转率逐渐增大，滑转率在最大差速状态e=5时仍小于20%，验证模型满足要求。根据仿真结果可知：当拖拉机在轻载高速工况行驶时，侧倾角对拖拉机的影响较大，为避免拖拉机侧翻，差速率可取较小值，以保证拖拉机的行驶稳定性。

综上仿真结果表明：当轮边驱动式电动拖拉机转向时，随着驾驶员期望的转向幅度增大，选取的差速率也会越大。差速率越大，则对应的转向半径越小，转弯的灵活性更好，但侧倾角、滑转率增大，会使拖拉机的稳定性变差。由于差速率变化会影响拖拉机的转向特性，为保证轮边驱动式电动拖拉机具有良好的转向特性，故需依据仿真得到的数据计算模型的差速率边界值和对应的最小转弯半径，合理设计差速率的最大取值范围。

表2为随差速率变化下的稳态仿真试验数据，其中，Δv为轮速差，rr为最小转向半径。

表2 稳态仿真试验数据

由表2可知：当差速率取值为5时，轻载高速工况的横摆角速度、最小转向半径、速度差和车轮外侧滑转率大于重载低速工况，而侧倾角和车轮内侧滑转率低于重载低速工况。随着差速率数值的增大，轻载高速工况的拖拉机与转向性能相关的各个参数逐渐增大。考虑到高速行驶的稳定性，横摆角速度、侧倾角、滑移率等参数不应过大，由于横摆角速度的变化率最大，故以横摆角速度为控制对象，计算差速率推荐的极限取值为6%～8%，对应的转向半径为13.13～17.50 m。当拖拉机以重载低速工况行驶时，拖拉机的各个参数随差速率也逐渐增大。由于拖拉机低速行驶时，需考虑转向的灵活性，转向半径应尽可能减小，故横摆角速度的最大值应偏大，但考虑到拖拉机在侧倾角较大时有侧翻的风险，故需平衡侧倾角和横摆角速度的取值，计算可知差速率推荐的极限取值为21%～23%，对应的转向半径为4.57～5.01 m。

轮边驱动式电动拖拉机轻载高速工况对稳定性的要求较高，当差速率推荐的取值为6%～8%时，对应的侧倾角为4.13°～5.37°，远小于最大侧倾角的取值范围，满足拖拉机对稳定性的要求。轮边驱动式电动拖拉机低速重载工况对转向灵活性的要求较高，东方红1804拖拉机的最小转向半径为6.02 m，对比可知重载低速工况的最小转向半径减小了24.09%，具有更好的机动性能。仿真结果验证了轮边驱动式电动拖拉机差速转向模型的可靠性，可为同类型差速转向系统提供差速率的最大取值范围和对应的最小转弯半径。

4 结论

(1)随着差速率变大，轮边驱动式电动拖拉机的轮速差、滑转率、横摆角速度和侧倾角变大，转向半径变小，转弯的灵活性更好，但稳定性变差。

(2)轮边驱动式电动拖拉机以重载低速工况行驶时，滑转率参数对拖拉机转向行驶的影响较小，但考虑到横摆角速度的最大取值，差速率的推荐取值为21%～23%，转向半径为4.57～5.01 m，相比东方红1804拖拉机的最小转向半径减小了24.09%。

(3)轮边驱动式电动拖拉机以轻载高速工况行驶时，当稳态侧倾角加大时，拖拉机容易侧翻，平衡侧倾角和横摆角速度的取值，差速率的推荐取值为6%～8%，对应的侧倾角为4.13°～5.37°，满足拖拉机对稳定性的要求。