尺寸效应下Cu-Ag合金强度的神经网络预测

张学宾，谷继华，宋克兴，米绪军，吴保安，肖 柱，解浩峰，吕长春

(1.河南科技大学 材料科学与工程学院，河南 洛阳 471023；2.有研工程技术研究院有限公司，北京 100088； 3.重庆材料研究院有限公司，重庆 400700；4.中南大学 材料科学与工程学院，湖南 长沙 410083；5.河南优克电子材料有限公司，河南 济源 454650)

0 引言

在集成电路封装、电子通信、连接器、音视频传输等领域，对键合线、线缆等丝线材传输信号的产品性能要求越来越高，细丝线材制造工艺受到国内外学者的关注[1-2]。在Cu-Ag合金微细丝拉拔生产中，容易出现拉断的现象，断裂与合金的力学性能有密切关系，因此有必要精确预测Cu-Ag合金抗拉强度。

粒子群优化(particle swarm optimization，PSO)算法和反向传播(back-propagation，BP)神经网络算法在数据处理领域已经获得广泛的应用[3-8]。BP算法建立在梯度下降法的基础上，实现输入输出间高度非线性映射关系。文献[9]把PSO算法应用于BP神经网络，并进行了能见度的预测，获得良好结果。文献[10]对PSO-BP进行改进并应用于客户流失警告信息的预测中。不少学者应用神经网络进行金属材料的研究，如文献[11]通过神经元网络得到Ni-Fe合金镀层性能指标的评价权重，证明粒子群算法优化的神经网络模型具有更高的预测精度。文献[12]将神经网络应用于新型Ti-Al-Zr-Nb-Mo-Si钛合金热变形行为和流变应力本构关系的构建，流变应力预测效果较好。文献[13-14]将神经网络应用于活性粉末混凝土强度和抗剪承载力等的预测，对活性粉末混凝土强度预测精度很高，对活性粉末混凝土梁抗剪承载力预测的结果可靠。但目前利用神经网络对Cu-Ag合金材料性能尤其是力学性能进行预测的研究不足。

本文通过Cu-Ag合金拉拔试验，获得不同线径和银含量(质量分数)时Cu-Ag合金材料的强度数据，构建了BP神经网络和PSO-BP神经网络，来预测Cu-Ag合金不同线径时的抗拉强度，以期对Cu-Ag合金在微细丝拉拔工艺方面的制定提供数据支撑。

1 Cu-Ag合金抗拉强度拉拔试验

1.1 试验准备与过程

采用不同银含量(质量分数，下同)、直径为7.18 mm的Cu-Ag合金连铸杆。本合金根据银质量分数不同分为Cu-1Ag(Ag质量分数1%，余量Cu)、Cu-2Ag(Ag质量分数2%，余量Cu)、Cu-4Ag(Ag质量分数4%，余量Cu)和Cu-20Ag(Ag质量分数20%，余量Cu)4种。连铸杆在拉丝机上进行大拉机多模连续拉制，拉拔成直径为3 mm的线材；然后，在中拉机上拉拔成直径为1.0～1.2 mm的丝材，进行在线连续退火；之后，在小拉机上拉拔成直径为0.25～0.30 mm的丝材；在细拉机上进一步拉拔成直径为0.08～0.10 mm的细丝；最后，在微拉机上拉拔成直径为0.05～0.02 mm的Cu-Ag合金微细丝材。

1.2 试验结果与分析

对各道次不同线径的Cu-Ag合金丝线材进行单向拉伸的抗拉强度试验，得到Cu-Ag合金丝线材的抗拉强度随线径的变化，如图1所示。

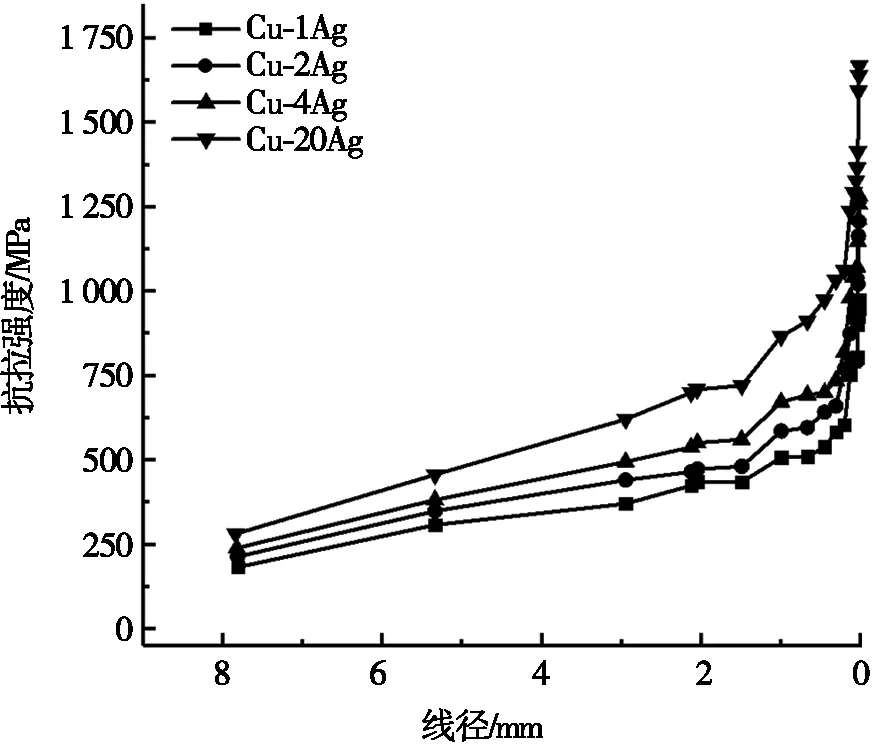
图1 Cu-Ag合金抗拉强度随线径的变化

由图1可知：在Cu-Ag合金微细丝的拉拔过程中，不同线径的Cu-Ag合金丝线材抗拉强度在不同阶段差异明显。以Cu-4Ag合金为例，直径为7.18 mm的铸态杆坯抗拉强度为239 MPa，从线径7.827 mm拉拔到1 mm时，抗拉强度缓慢增加到672 MPa，抗拉强度平均增幅为63.4 MPa/mm。在后续的拉拔中，当线径小于1 mm时，合金的抗拉强度随着线径的减小迅速增加，线径从1 mm减小到0.02 mm时，抗拉强度从672 MPa增加到1 283 MPa，抗拉强度平均增幅为623.5 MPa/mm，此时线径的变化明显影响合金的抗拉强度，表现出明显的尺寸效应。因此，在Cu-Ag合金微细丝拉拔生产过程中，当Cu-Ag合金细丝直径小于1 mm后，尺寸效应是一个不可忽略的重要问题。所以，本文基于尺寸效应建立神经网络模型，用来预测Cu-Ag合金的抗拉强度随线径的变化。

图2为不同线径Cu-4Ag合金丝线材的横截面微观组织。从图2a中可以看出：Cu-4Ag合金铸态杆坯(直径为7.18 mm)组织主要由共晶树枝晶和共晶群体组成，小共晶团均匀分散在枝晶臂间，枝晶间亮白色质点为Ag颗粒的偏聚。从图2b中可以看出：当铸态杆坯拉拔至线径为5.34 mm时，由于变形量仅为44.7%，Cu-4Ag合金丝线材的微观组织在拉拔力作用下发生变化，但仍保留了大量铸态枝晶组织，枝晶间距排列更加规则，枝晶间Ag颗粒分布更加均匀，丝线材宏观力学性能稳步提升，抗拉强度由铸态的239 MPa增加到382 MPa。随着拉拔的持续进行，当线径减小到1 mm时，Cu-4Ag合金丝线材的总变形量达98.06%，其微观组织发生显著变化，枝晶组织基本消失，以变形态的细小等轴晶组织为主，且整体组织均匀致密，如图2c所示，宏观上材料由于形变硬化使得力学性能显著增加，线径为1 mm的Cu-4Ag合金丝线材抗拉强度达672 MPa。因此，微观组织的演变规律，再次验证了Cu-4Ag合金丝线材在连续拉拔过程中随着线径减小出现尺寸效应。

2 Cu-Ag合金BP模型

2.1 Cu-Ag合金BP模型的建立

将试验得到的285组Cu-Ag合金样本数据分为训练样本、验证样本和测试样本，分别占总样本数的 70%、15%和15%。其中，训练样本是用来进行神经网络的训练，验证样本主要是用来分析神经网络的准确度，测试样本则主要用来测试BP人工神经网络模型的适用性。然后对Cu-Ag合金样本数据进行预处理，预处理使用mapminmax 函数[15]，使Cu-Ag合金样本数据归一化到[-1，1]，归一化采用式(1)进行：

(1)

BP神经网络是按预测误差反方向传播的神经网络，主要包括输入层、输出层和隐含层，通过调整网络中隐含层的连接权重和阈值提高神经网络的学习能力，更好地实现非线性映射关系。根据BP人工神经网络的算法机理可知：选择输入层到隐含层的激活函数为tansig(n)函数，隐含层到输出层的激活函数为purelin(n)函数。为了减少计算时间、减小占用内存的大小、加速收敛速度等，综合考虑选用L-M算法[16]。在模拟过程中，设定一个val fail值来表征神经网络的训练效果，神经网络系统根据val fail值判断误差信号连续不下降的次数，进而结束训练，这个数值一般取20[17]。

建立BP神经网络模型需要确定模型的拓扑结构。通过对影响Cu-Ag合金抗拉强度的分析，确定BP人工神经网络的输入参数为Cu-Ag合金的丝线材直径和银元素的质量分数，输出参数则为抗拉强度。神经网络隐含层神经个数采用经验公式[18]确定，如式(2)所示：

(2)

其中：h为隐含层神经元个数；m为神经元网络输入层节点个数，因输入参数为Cu-Ag合金的丝线材直径和银元素质量分数，取m为2；n为神经元网络输出层节点的个数，因输出参数为Cu-Ag合金的抗拉强度，n取1；α为调节常数，一般取值1～10[19]。通过经验公式来确定需要“试错”的神经个数为3～12，并通过建立多个神经元网络模型进行模拟训练，利用皮尔逊(Pearson)相关系数R考察抗拉强度目标值和神经元网络模型输出值之间的相关性[20]，结果如表1所示。由表1可知：当隐含层神经元个数h为10时，相关系数R最大且最接近于1，说明网络训练效果好。综上所述，确定Cu-Ag合金丝抗拉强度人工神经网络模型最优的拓扑结构为：m-h-n=2-10-1。

表1 不同神经元个数对应的相关系数R值

图3 BP神经网络模型训练次数与均方差的关系

2.2 Cu-Ag合金BP神经网络模型结果分析

图3为BP神经网络模型训练次数与均方差的关系。从图3可以看出：随着迭代次数的增加，均方差迅速降低。模型迭代至62次时，验证样本数据均方差达到最小值，模型验证样本数据的均方差不再减小。虽然在第25次和第50次迭代过程中Cu-Ag合金验证样本数据的均方差出现增大现象，但随着迭代过程的继续进行，Cu-Ag合金验证样本数据的均方差继续下降，直至迭代次数为68次时，验证样本数据的均方差趋于稳定，说明Cu-Ag合金样本数据训练过程中并没有出现过多的局部最优现象，BP神经网络模型较为合理稳定。

图4为对样本数据抗拉强度目标值和BP神经网络模型输出值的相关性分析，散点数据为拉拔试验数据，直线为拟合数据。分别对训练样本、验证样本、测试样本和总样本数据进行拟合，得相关系数R(即拟合线斜率)分别为0.782、0.804、0.832、0.794，如图4a～图4d所示。相关系数R都较高，说明抗拉强度目标值与神经网络的输出数据之间具有较好的相关性。表2为BP神经网络模型测试样本数据中提取的6组样本实测数据和模型计算的抗拉强度相对误差。从表2中可以看出：抗拉强度最大相对误差绝对值为9.8%，最小相对误差绝对值为1.1%，相对误差绝对值均在10%以内。因此，建立的BP人工神经网络模型稳健，能够预测抗拉强度的变化。

表2 BP神经网络计算的抗拉强度和实测抗拉强度相对误差

3 Cu-Ag合金PSO-BP模型

3.1 PSO-BP算法流程

PSO-BP神经网络模型的基础是粒子群算法，速度更新式与位置更新式[21]分别如式(3)和式(4)所示：

(3)

(4)

其中：v为速度；x为位置；w为惯性因子；c1、c2为学习因子；pbset为个体最优位置；gbset为全局最优位置。

3.2 Cu-Ag合金PSO-BP模型的建立

用于PSO-BP神经网络训练的样本数据为Cu-Ag合金抗拉强度试验得到的285组样本数据，输入参数为Cu-Ag合金的丝线材直径和银质量分数，输出参数为抗拉强度。PSO-BP神经网络模型在训练前，对粒子群优化算法进行参数设定[22]：在种群初始化的过程中，种群粒子数目通常选取20～40，本文种群粒子数目选取30。学习因子(加速常数)则表示种群中的粒子个体向着自身和全局最优极值点靠近的加速度的权值，通常两个学习因子的数值设置一样，取值为c1=c2=2；最大迭代次数设置为500次，最小的训练停止误差为10-5；结构依然采用之前优选出的2-10-1的3层神经网络结构。输入层到中间隐含层的激活函数选用tansig(n)函数，中间隐含层到输出层的激活函数选用purelin(n)函数。种群粒子的最大速度与最小速度决定种群粒子每次的移动距离和向周围区域扩展的能力。种群粒子飞行速度要控制在[-1，1]，初始学习速度设置为0.1，种群粒子位置控制在[-1.5，1.5]。根据PSO-BP神经网络的算法流程和参数设置，利用MALLAB软件编程，进行神经网络的模拟训练。

3.3 Cu-Ag合金PSO-BP模型结果分析

图5 抗拉强度目标值与PSO-BP神经网 络输出值相关性

图5为对抗拉强度目标值与PSO-BP神经网络模型输出值的相关性分析结果。散点数据为拉拔试验数据，直线为采用PSO-BP神经网络模型输出进行拟合的数据。得到PSO-BP神经网络进行抗拉强度训练的相关系数R(即拟合线斜率)为0.907，明显高于BP人工神经网络的样本数据的相关系数(0.794)。

表3为基于 PSO-BP 人工神经网络模型测试样本数据中提取的6个线径所对应的抗拉强度数据和模型计算得到的抗拉强度数据的相对误差。从表3可以看出：实测与模型计算抗拉强度的最大相对误差绝对值为3.3%，最小相对误差绝对值为0%，相对误差都在5%以内。而BP神经网络模型最大相对误差绝对值为9.8%，最小相对误差绝对值为1.1%。两模型相比较，得出基于 PSO-BP人工神经网络抗拉强度模型预测的Cu-Ag合金抗拉强度更为准确。

表3 PSO-BP神经网络计算的抗拉强度和实测抗拉强度相对误差

4 结论

(1)在Cu-Ag合金微细丝的拉拔过程中，不同线径的Cu-Ag合金丝线材抗拉强度在不同阶段差异较大，表现出明显的尺寸效应。

(2)Cu-4Ag合金铸态杆坯组织由共晶树枝晶和共晶群体组成，小共晶团均匀分散在枝晶臂间；初期拉拔阶段，保留了大量铸态枝晶组织；当总变形量达98.06%时，枝晶组织基本消失，以变形态的细小等轴晶组织为主，且整体组织均匀致密。

(3)确定Cu-Ag合金丝抗拉强度人工神经网络模型最优的拓扑结构为2-10-1。

(4)建立了BP神经网络和PSO-BP神经网络模型，对Cu-Ag合金丝抗拉强度进行预测，两种模型的样本数据相关系数R分别为 0.794和0.907，PSO-BP神经网络模型更为稳健。PSO-BP神经网络模型测试样本数据最大相对误差绝对值仅为3.3%，能准确预测Cu-Ag合金的抗拉强度。