能量法结合数值模拟的20SiMn合金钢粗糙度分析

陈 爽，肖锦初，张 志，肖友谱

(江西理工大学 机电工程学院，江西 赣州 341000)

0 引言

20SiMn合金钢作为水轮机主轴材料在各大水电站中普遍使用，其中，表面粗糙度过高会使零件更容易磨损，从而影响其力学性能，使发电机组不能安全、平稳、高效运行[1-3]。因此，降低20SiMn合金钢表面粗糙度和进行粗糙度分析，对保证零部件的安全可靠具有重要意义。

目前，国际上广泛使用的表面粗糙度测量方法主要有比较法[4]、触针法[5]、光切法[6]和激光散斑法[7]等。文献[8-11]提出了一系列预测表面粗糙度的模型，但这些模型大多是基于试验结果或几何关系建立的。文献[12]把二代提升小波用于滤波的方法，让表面粗糙度信息的提取计算更快、更便捷。文献[13]为实现表面粗糙度的无损测量，提出了一种基于激光位移传感器的粗糙度测量系统。文献[14]利用图像算法分析，将反向传播(back propagation,BP)神经网络系统实验值与粗糙度参数进行对比，间接计算粗糙度。文献[15]基于超声波射入到粗糙表面的自由应力边界条件，用返回的幅值与离差率表征粗糙度。可迄今为止，很少有将材料内部应变能变化情况与表面粗糙度联系起来的研究报道。本文将能量法与数值模拟结果相结合，分析了20SiMn合金钢在不同静压力参数下，进行超声振动挤压强化后表面粗糙度的变化情况。

1 能量法与粗糙度的关系

为研究材料表面粗糙度，以能量法中的卡氏定理(Castigliano’s theorem)[16-17]为理论基础，可以搭建出系统中应变能与材料表面形变位移的关系，如式(1)所示，由材料的表面形变位移δ可以计算出材料表面各节点的微位移变化情况[18]。

(1)

其中：δ为表面形变位移,μm；Vε为应变能,J；F为施加在材料上的力,N。

因在整个加工过程中材料都处在被压缩的状态，所以计算应变能Vε时，使用压缩状态下的应变能计算公式，如式(2)所示。

(2)

其中：FN为材料表面的挤压力,N；E为弹性模量,MPa；A为材料的横截面积,m2。

将式(2)代入到式(1)中，可以得到在每个应变能峰值时微位移的计算公式：

(3)

通过式(3)求得每个应变能峰值时的微位移δ1，δ2，δ3，…，δn，代入粗糙度计算公式(4)，可求得通过应变能数值计算出的表面粗糙度Raii。式(5)用于计算粗糙度模拟值Rai。

(4)

(5)

其中：Raii为通过应变能数值计算出的粗糙度,μm；δi为通过各节点应变能计算出的微位移与基准线的差,μm；Rai为粗糙度模拟值,μm；yi为有限元模拟中各节点微位移与基准线的差,μm。

2 有限元分析结果与讨论

2.1 ABAQUS仿真模型建立

本试验中采用直径为5 mm的球型加工工具刀头，被加工零件是长宽均为50 mm、厚度为16 mm的长方体20SiMn合金钢块料。考虑到主要研究对象为块状物体，因此网格精度要求较高。有限元模型采用八节点线性减缩积分C3D8R进行网格划分，滚挤压球与材料表面接触类型设为Surface to Surface Contact，由于实际强化过程滚压球理论上可以自由转动，所以取摩擦因数为滚动摩擦因数0.01。应力应变场在整个强化模拟过程中是对称分布的，为提高运算效率，可建立1/2等效有限元模型进行仿真实验，整个模型单元数量为126 804个。20SiMn合金钢超声振动强化有限元模型图如图1所示。

图1 20SiMn合金钢超声振动强化有限元模型图

2.2 仿真实验参数

本试验选用的工具头材料为硬质合金，将其定义为刚体，并且假设工具头不会在加工过程中产生弹塑性形变，设定参数是各向同性线性弹性参数。工具头材料参数设定为：密度ρ=15×103kg/m3；弹性模量E=710 GPa；泊松比ν=0.21。被加工材料20SiMn合金钢的密度ρ=7.85×103kg/m3；弹性模量E=200 GPa；泊松比ν=0.3。

3组仿真实验中的加工参数为：进给速率均为0.6 mm/min；静压力参数为变量，分别为100 N、300 N、600 N。在超声挤压强化的过程中，需要在开始阶段使工具头与被加工材料接触，并且对材料分别施加100 N、300 N和600 N的静压力，之后通过变幅杆对工具头施加6 μm的振幅，通过静压力与振幅的叠加效果来加工零件。在整个仿真过程中，静压力和振幅共同作用在材料表面，参照文献[19-20]，可把6 μm振幅等效为200 N的冲击力。

3 有限元仿真结果与分析

3.1 计算表面粗糙度模拟值

表面粗糙度随加工参数的变化并不是单调的，在分析静压力对表面粗糙度影响之前，需研究超声振动加工过程中材料表面轮廓的变化规律。加工过程中涉及多个冲击动作，所以在表面提取路径时采用单点冲击有限元模型，相邻的冲击坑中心沿着Z轴分布，材料表面轮廓的提取路径如图2中红线所示。

在超声加工过程中，静压力参数是决定材料表面加工能量的重要参数。本文单独考虑静压力参数变化对超声冲击后表面轮廓的影响。当振幅为6 μm，静压力分别取100 N、300 N和600 N时，经ABAQUS软件模拟冲击过程，并提取单次冲击作用后的路径数据，不同静压力参数下单次冲击的冲击坑形貌如图3所示。

图2 表面轮廓的提取路径

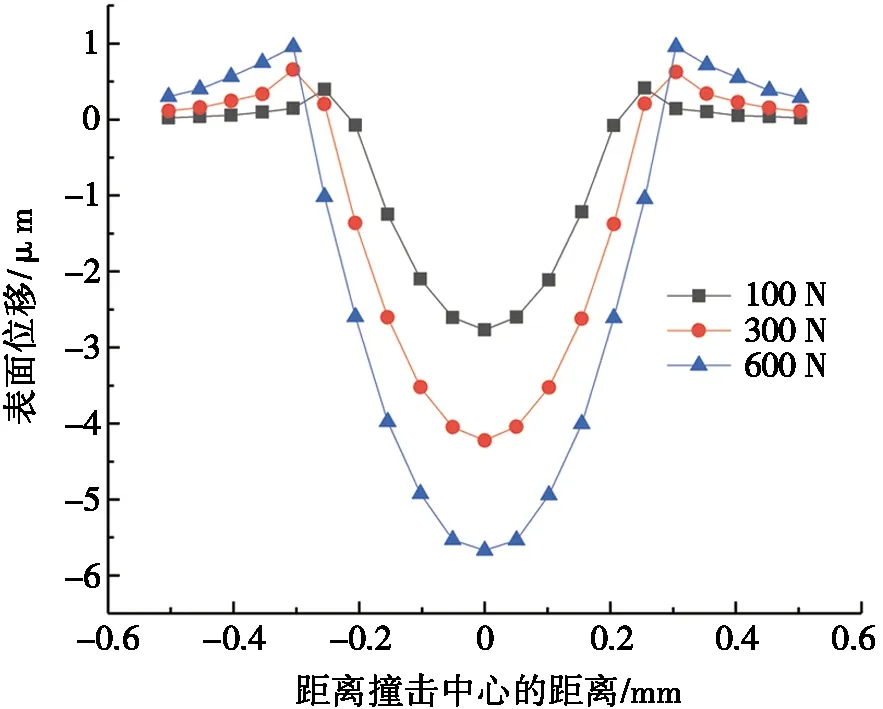
图3 不同静压力参数下单次冲击的冲击坑形貌

由图3可以看出：随着静压力的增加，冲击坑的深度和宽度都显著增加。当被加工材料表面较为粗糙时，将静压力参数适当增大，有利于降低表面粗糙度。

图4 静压力参数为100 N，6 μm时表面轮廓位移

为了计算表面粗糙度模拟值Rai，需在静压力分别为100 N、300 N、600 N时，其他加工参数不变的情况下，对材料往返加工6遍。使用与提取单次冲击路径一样的方法，因在不同静压力参数下表面轮廓的提取与粗糙度计算方法一样，所以只给出静压力参数为100 N，6 μm时表面轮廓位移，如图4所示。

由图4可知：经超声滚压加工后，材料表面仍存在微小的峰谷不平度，且不同加工参数的表面形貌存在显著差异，但相同加工参数下的峰谷差值相对稳定。表面位移绝对值随着静压力的增加而增加。通过观察图4的数据，结合式(4)可计算得到静压力参数为100 N时的表面粗糙度模拟值，以相同方法计算静压力参数分别为100 N、300 N和600 N时的粗糙度模拟值。当静压力参数为100 N时，Ra1≈0.233 μm；当静压力参数为300 N时，Ra2≈0.217 μm；当静压力参数为600 N时，Ra3≈0.358 μm。

从以上计算结果可见：当有限元仿真静压力参数为300 N时，经超声加工后的20SiMn合金钢材料表面粗糙度最低，且Ra1、Ra2、Ra3粗糙度值由大到小排序为Ra3>Ra1>Ra2。

3.2 通过内部应变能计算粗糙度模拟值Raii

使用ABAQUS有限元仿真软件对超声加工过程进行模拟，在仿真软件内部分别提取静压力参数为100 N、300 N和600 N的情况下，20SiMn合金钢超声加工后材料内部应变能的变化数据，绘制时间与应变能变化曲线，不同静压力参数加工后材料内部应变能如图5所示。

由图5可知：材料内部的应变能数值在0 s时就到达第一个峰值，每个应变能峰值出现时就是材料被冲击的时刻，应变能的平均值随静压力参数的增大而增大。因为超声加工开始之前工具头就要给材料施加一个静压力，所以应变能第一个峰值大小会随静压力的增大而增大，第一个应变能峰值出现时超声加工还没开始，因此需要去除第一个峰值数据进行计算。提取除第一个峰值外的峰值能量数据，代入式(3)中，使用MATLAB软件计算得δi，再将δi代入式(5)中，可求得通过应变能反映出的材料表面粗糙度Raii。经MATLAB软件处理后的结果：静压力参数为100 N时，Ra11≈0.813 μm；静压力参数为300 N时，Ra22≈0.750 μm；静压力参数为600 N时，Ra33≈1.592 μm。粗糙度Ra11、Ra22和Ra33由大到小排序为Ra33>Ra11>Ra22，与有限元模拟得到的粗糙度排序结果一致。比较应变能反映出的粗糙度Raii与有限元粗糙度模拟值Rai可知：数值大小有明显的差距。差值产生的主要原因是：从超声加工过程中静压力的施加方式分析，在整个仿真过程中，工具头对材料持续施加恒定静压力，在静压力与冲击作用下，以冲击点为圆心向四周不断扩大发生弹性形变且无法弹性恢复，这部分弹性应变能会使材料内总应变能偏大，从而使计算得到的微位移与Raii偏大。但是不影响通过材料内部应变能变化曲线来分析表面粗糙度在不同静压力参数作用下的大小。

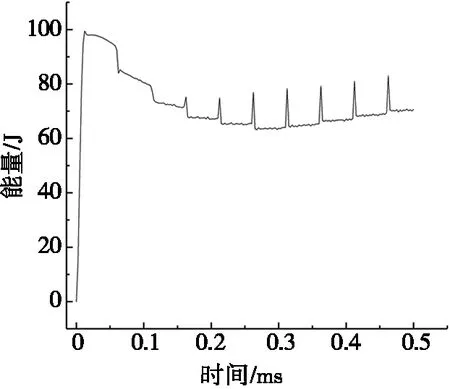
(a) 静压力100 N时应变能 (b) 静压力300 N时应变能(c) 静压力600 N时应变能

4 试验验证

试验采用的设备是山东豪克能HVMG500系列的超声强化立式加工中心。该装置由数字超声波发生器和执行部件组成，其中，执行部件主要由加工工具头、变幅杆和换能器3个部分组成。

本试验使用的加工材料是20SiMn合金钢，其化学成分如表1所示。

表1 20SiMn合金钢化学成分 %

选取20SiMn合金钢进行超声振动挤压试验，表2为在不改变4个影响因素时，单独改变静压力参数处理后表面粗糙度Ra的值。

表2 不同静压力参数下的试验结果

由表2可知：在只改变静压力参数，其余参数不变的情况下，当静压力参数为300 N时，表面粗糙度最低，与有限元模拟结果和通过应变能变化预测的粗糙度变化情况保持一致。综上所述，证实以能量法中的卡氏定理为理论基础搭建的关系式，能通过加工过程中应变能的变化预测出被加工材料表面的粗糙度变化情况，表明应变能可以用于分析粗糙度值。

5 结论

(1)经超声滚压加工后材料表面仍然存在微小的峰谷不平度，且在进行单点冲击时，冲击坑两边会出现材料的堆积现象。被加工件表面比较粗糙时，选取较大静压力参数可有效降低材料表面的粗糙度。

(2)在有限元仿真中，当静压力参数分别为100 N、300 N和600 N时，粗糙度仿真模拟值Rai与Raii的变化规律一致。

(3)以能量法中的卡氏定理为理论基础搭建的关系式，可以通过加工过程中应变能的变化情况，分析出被加工材料表面的粗糙度变化情况。