基于MODFLOW-SUB建立变渗透系数的地下水流-地面沉降模型

孟世豪，崔亚莉，田 芳，罗 勇，石鸿蕾

1.中国地质大学(北京)水资源与环境学院，北京 100083 2.北京市水文地质工程地质大队(北京市地质环境监测总站)，北京 100195

0 引言

由地下水开采引起的地面沉降过程十分复杂，土体的压缩变形将导致其孔隙比和渗透系数都产生相应的变化，进而影响沉降特征。数值模拟是研究及预测地面沉降演变规律的重要手段[1-7]，为了模拟实际固结沉降过程，不同学者尝试采用不同的方法来解决变参数下的模拟问题，例如：Joseph[8]利用有限元法讨论了变参数的一维固结问题；Chen等[9]采用积分差法刻画了多层黏土一维非线性固结问题；叶淑君等[10]基于修正的麦钦特模型研发了变参数的地面沉降模拟软件；刘波等[11]、李莎等[12]利用COMSOL建立了基于Kozeny-Carman方程的变渗透系数沉降模型；Xu等[13]、常啸[14]基于修正的剑桥模型利用有限元方法对软基固结进行了分析。从前人研究成果来看，众多学者均是根据所选择的方法及具体的地质、水文地质条件自主编程完成对地面沉降压缩固结的模拟，广泛推广的可行性较弱；而COMSOL软件对地下水补给径流排泄刻画较为粗糙，普适性不强。在广泛应用的MODFLOW软件中嵌入地面沉降SUB模块，可用来模拟源于地下水开采造成的区域地下水流-地面沉降过程，但在SUB中设定黏土层的垂向渗透系数为常数，无法真实再现地面沉降随时间延长的压缩固结过程。

综合以上因素，在充分分析前人有关沉降过程中渗透系数变化规律研究成果的基础上[15-21]，本文结合吕卫清等[18]通过试验结果拟合描述土体渗透性变化的关系式对MODFLOW-SUB进行改进，建立了变渗透系数的地下水流-地面沉降耦合模型。并以美国地质调查局建立的加州羚羊谷模型[22]为基础，设计典型算例，在相同条件下，分别以常渗透系数和变渗透系数对该地进行模拟，对比两者累计沉降量和压缩释水量的差异；同时通过数值模拟实验，设定不同开采量和不同夹层厚度，分析不同条件下夹层内垂向渗透系数变化对沉降差值的影响，以期对改进前后模型的适用性作出评价。

1 基于MODFLOW-SUB建立的地下水流-地面沉降耦合模型

MODFLOW是一套广泛用于孔隙介质中地下水流动数值模拟的软件[23]。SUB程序包是MODFLOW中基于太沙基一维垂向有效应力原理的沉降模块，可模拟由于夹层中地下水的排泄而造成的含水系统的压缩，也可模拟弱透水层的排水和压缩的滞后现象。

通过MODFLOW可建立地下水流模型，利用SUB可建立地面沉降模型[24]。在水流模型中，源汇项的改变会导致含水层水头发生改变，水头的改变在地面沉降模型中会产生相对应的沉降，在沉降压缩过程中又会释放一部分水量，这部分释水量又会进入水流模型的源汇项中，最终完成地下水流模型与地面沉降模型的耦合。

由于构成夹层的沉积物(一般为黏土、亚黏土、粉土类)渗透系数较低，因此，在含水层系统中夹层的水头变化通常滞后于周围含水层的水头变化。当含水层水头下降时，夹层内的水头无法立即与含水层水头保持一致，此刻，含水层和夹层会产生一个水头差，通过这个水头差，从夹层的中间界面向两边含水层排水，完成双面排水过程。

通过对消散夹层与含水层的水头差过程进行求解[25]，可以得到表示滞后的时间常数τ0，其表示了在给定水头变化下，所有沉降完成93%时所需要的时间[26]：

(1)

(2)

通过式(1)和式(2)可以发现：夹层内垂向渗透系数和厚度的改变会影响夹层压缩释水的过程，影响沉降的滞后性，从而影响夹层的沉降量；且夹层厚度越大，影响程度越大。

2 SUB源代码的改进

SUB程序包包含5个主要的子程序，分别为数据的读取、水头的调整、公式的迭代计算、均衡计算和结果输出。改进思路是在水头调整完成之后，让夹层内垂向渗透系数根据夹层内水头变化发生相应改变。

针对沉降过程中渗透系数的变化规律，很多学者[13, 28-30]通过试验总结出了渗透系数与孔隙度、平均孔径、塑性指数等参数的关系式，但在SUB程序包中，未对夹层的这些参数进行定义，其关系式无法很好地与模型进行耦合。而吕卫清等[18]从固结系数的定义出发，将压缩系数视为变量，建立了渗透系数与固结应力的微分方程，并通过试验数据建立了渗透系数与有效应力σ′的关系式：

(3)

本次研究利用有效应力变化与水头变化的关系将式(3)进行进一步推导，得到夹层内渗透系数与水头的变化规律(式(4))。

(4)

式中：ρw为水的密度(kg/m3)；g为重力加速度(m/s2);h′ 为当前夹层内水头(m)；hc为夹层内预固结水头(m)。

式(4)中以夹层内中心水头为自变量，可以很好地耦合到SUB建立的地面沉降模型当中，完成对夹层内垂向渗透系数的调整。

对SUB程序包的改进主要包括以下3部分：

1)创建新的数组使得每个网格都获得单独的夹层内垂向渗透系数。在SUB中，夹层中的垂向渗透系数是以参数区的形式赋值，即多个网格共用一个垂向渗透系数值。想要使每个网格的夹层内垂向渗透系数能够随着该网格水头的变化而变化，首先要设定一个新的数组使每个网格都获得单独的垂向渗透系数。

2)创建新的子程序GWF2SUB7YHK来完成夹层内变渗透系数的功能，并把该子程序插入到参数数据读取之后、公式迭代计算之前(图1)。在改进的子程序中读入每个夹层网格的垂向渗透系数、初始预固结水头和当前应力期水头，并按照式(4)求得对应当前应力期水头的新垂向渗透系数，使得夹层内的渗透系数可以随着水头的变化而变化，即完成变渗透系数的调整。

3)在运行改进后的软件时，需要填写新的输入文件。输入文件所需要内容包括：①改进式(4)中所需的常数参数C，其可以根据不同地区的黏土性质进行计算；②控制输出某个网格某个应力期夹层内垂向渗透系数的参数。

图1 SUB改进后的逻辑框图

3 变渗透系数模型的验证分析

3.1 典型算例建立

研究区位于美国加州羚羊谷流域(图2)，羚羊谷是莫哈韦沙漠西部的一个地形封闭盆地，位于洛杉矶东北约80 km处。羚羊谷地下水盆地面积约为2 400 km2。地下水流系统由两个含水层组组成：第一含水层组为潜水含水层，厚度为150～275 m，主要接受降雨和边界流入补给；第二含水层组为承压含水层，厚度为480～600 m，在开采条件下可得到上部潜水的越流补给，与第一含水层组水力联系密切。模型被离散成一个由43行60列组成的网格(图3)。模拟的时间跨度为80 a，从1915—1995年，第一年为稳定状态。

图2 研究区位置示意图[22]

典型算例以美国地质调查局建立的加州羚羊谷模型为基础，地层结构参数和边界条件与原模型保持一致(表1、2)，对源汇项进行简化，只在盆地中心地区的第二含水层(图3b)设置固定开采量(8 500 m3/d)，设置夹层初始水头和初始预固结水头与含水层初始水头一致。针对上述地质结构和条件分别进行了变渗透系数和常渗透系数的模拟。

3.2 模拟结果分析

在原MODFLOW2005(常渗透系数)的模拟下，经过80 a的定量抽水，在抽水区域形成了降落漏斗和沉降漏斗(图4)。水位降深最大值为60.4 m，沉降量最大值为350.5 mm。

a. 第一含水层；b. 第二含水层及开采范围。

表2 夹层参数

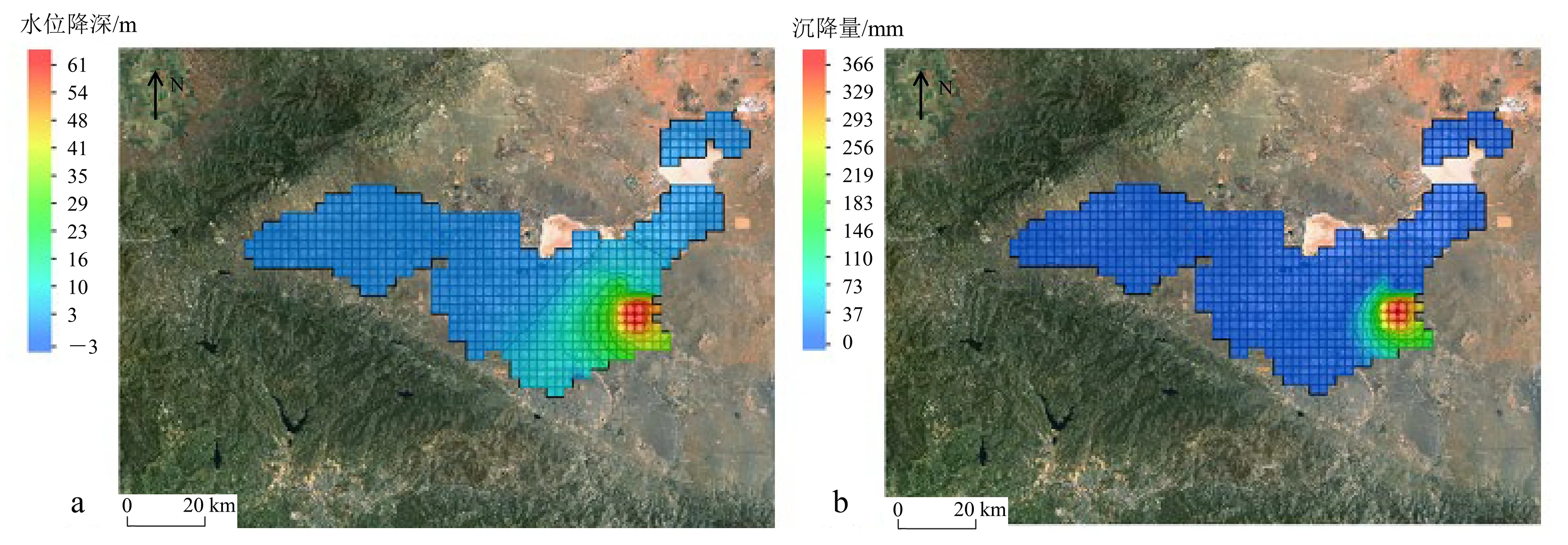
a. 最终水位降深(1995-12-31T20:15:00)；b. 最终地面沉降量(1995-12-31T20:15:00)。

在变渗透系数的模拟下，含水层水位变化与常渗透系数模拟基本相同，但其夹层内水位和沉降量均有减小。下面对第二含水层(承压含水层)降落漏斗和沉降漏斗中心网格(23，46)不同结果进行对比分析。

1)夹层内垂向渗透系数

由常渗透系数和变渗透系数模拟下夹层内垂向渗透系数对比分析(图5a)可以看出：模拟前期(0～20 a)由于滞后夹层中水头变化不大，因此两种模拟情况下垂向渗透系数变化都很小；随着抽水的持续进行，含水层中水头不断下降，导致夹层内压缩释水不断进行，夹层中的水头不断下降，在20 a后变渗透系数模拟下垂向渗透系数发生显著变化，其中在20～35 a中夹层内变渗透系数模拟下垂向渗透系数下降速度很快，随后下降速度减缓，至模拟期结束(80 a)，变渗透系数模拟下垂向渗透系数减小了2个数量级。

2)夹层内压缩释水量

在抽水初期，含水层水头下降快，从第二含水层每个应力期的压缩释水量变化对比(图5b)中可以看出：常渗透系数模拟下，夹层的压缩释水量逐渐增大，在第15 a达到最大压缩释水量19.5 m3；随着降落漏斗的增大，含水层水头下降速度减缓，夹层内压缩释水量也逐渐减小。变渗透系数模拟下，压缩释水量变化趋势与改进前一致，随着垂向渗透系数的减小，夹层释水过程变得困难；在第20 a，夹层内垂向渗透系数发生明显差别的同时，其压缩释水量也明显减小；模拟80 a后，累积压缩释水量比常渗透系数模型少了393.6 m3，约减少45.1%。

3)夹层内中心水头

常渗透系数模拟下，夹层内中心水头由725 m下降至678 m(图5c)。变渗透系数模拟下，由于夹层内垂向渗透系数的减小，压缩释水能力减弱，夹层内的水头消散速度也相对延缓，夹层内最终水头为692 m。

4)累计沉降量

随着夹层内垂向渗透系数的逐渐减小，变渗透系数模型的压缩释水量逐渐减少。根据算例的模拟结果来看，变渗透系数模型的最终沉降量(图5d)也会相对减少，依据本算例中模拟80 a地面沉降量来看，改进后的第二含水层累计沉降量比改进之前的总沉降量减少了大约15.6%。

通过以上对比分析可以发现，两个模型在20 a内，计算结果具有较好的一致性；而20 a后，两个模型计算结果差别逐渐显现出来，说明在这种水文地质条件和开采条件下，由于黏性土夹层压缩造成的垂向渗透系数的变化滞后20 a左右。

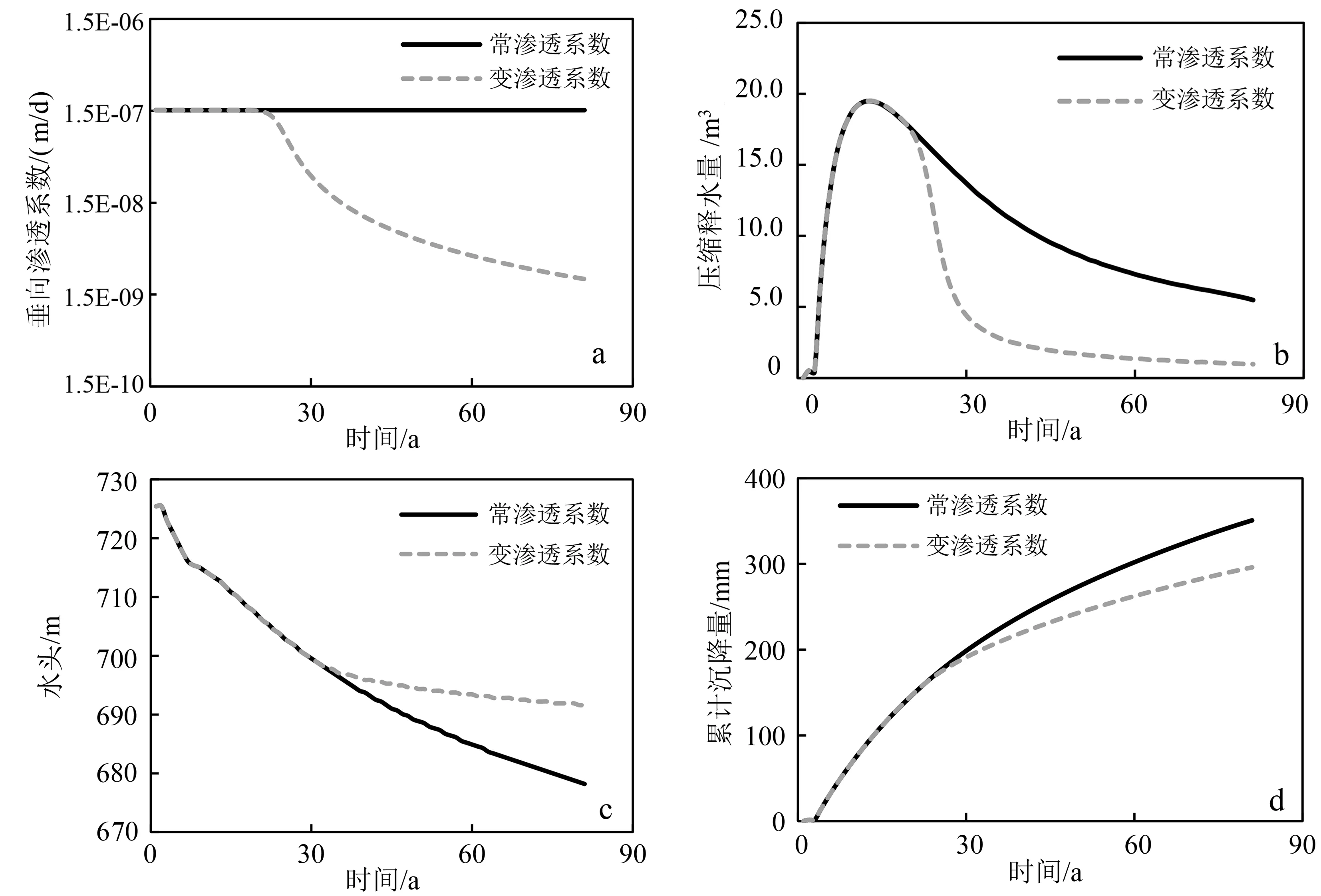
a. 夹层内垂向渗透系数；b. 逐应力期压缩释水量；c. 夹层内中心水头；d. 累计沉降量。

4 数值模拟实验

4.1 不同开采量对沉降的影响

为探究在不同开采量下夹层内垂向渗透系数变化所导致的沉降差值大小，设定开采量分别为0.85×104、1.42×104、1.98×104、2.55×104m3/d。

由80 a模拟结果显示，随着开采量的增加，水头下降速度和下降幅度都会加大，夹层内垂向渗透系数(图6)发生明显差别的时间由第20 年逐步提前至第8 年，最终垂向渗透系数值依次减小。

图6 研究区第二含水层夹层内垂向渗透系数变化对比

在第二含水层的累计沉降量增大的同时，沉降量累计变化幅度(沉降差值比)也由15.6%逐步增大到28.7%(图7)。由此可见，随着地下水开采量加大，两个模型计算的地面沉降量的差异越来越大，即夹层内垂向渗透系数的变化对沉降差值的影响程度增大。

图7 研究区不同开采量下第二含水层沉降量对比

4.2 不同夹层厚度对沉降的影响

为了探究在不同夹层厚度下，夹层内垂向渗透系数变化所导致的沉降差值大小，分别设定第二含水层中夹层厚度为0.7、1.4、2.1、2.8、3.5、4.2 m(图8，9)。其余参数不变，将模拟时间延长至400 a，80～400 a间水位基本保持稳定。

在不同夹层厚度的模拟过程中，其含水层水头变化相同，但随着夹层厚度的增加，压缩释水的滞后性不断增大。前80 a水位变化所造成的沉降，0.7 m厚度的夹层需要到第100 年可以全部完成，而4.2 m厚度的夹层需要到400 a左右才全部完成。

通过对比400 a内不同夹层厚度对应的沉降差值比(图9c)可以发现，当设定夹层厚度为1.4 m时，常渗透系数模型和变渗透系数模型的沉降差值在前25 a内基本保持一致，25 a以后，沉降差值比逐渐增大，在第100 年时完成全部沉降，最终沉降差值比为19.4%；而当夹层厚度扩大3倍，达到4.2 m时，两模型在第75 年产生差异，最终在第400 年完成全部沉降时沉降差值比达32.4%。

随着夹层厚度由0.7 m增加至4.2 m，两模型计算的沉降量产生差异的时间从第17 年逐渐滞后到第75 年。当模拟时间达到400 a时(图9b)，最终的累计沉降量随着夹层厚度呈线性增加，同时两模型的沉降差值比由11.6%上升到32.4%。

由此表明，随着夹层厚度的增大，两个模型计算的地面沉降量的差异越来越大，即夹层内垂向渗透系数的变化对沉降差值比的最终影响也会增大。

在众多的实际应用中，由于监测资料的限制，大多数模型的模拟时间往往在几十a，不足以完整体现沉降的滞后性。在本算例中，由80 a内不同夹层厚度对应的垂向渗透系数变化对比(图8)可以看出，夹层厚度的增加导致夹层内垂向渗透系数发生显著差别的时间逐步延迟。由于夹层厚度增加导致的滞后性，由垂向渗透系数变化所导致的沉降变化幅度(图9a)先由9.7%上升至17.3%，再下降至1.8%。虽然在第80年夹层厚度为4.2 m的沉降差值比仅1.8%，但在随后的50 a中，其沉降差值比迅速增长，忽略垂向渗透系数的变化会导致模型的预测和应用产生较大误差。

图8 研究区第80 年不同夹层厚度下第二含水层夹层内垂向渗透系数对比

a. 第80年累计沉降量及差值对比；b. 第400年累计沉降量及差值对比；c. 400 a内不同夹层厚度沉降差值比变化对比。

5 结论与建议

1)通过对SUB源代码的改进，建立起变渗透系数模型。通过典型算例的模拟分析，改进后的变渗透系数模型的最终结果(夹层垂向渗透系数、压缩释水量、夹层内中心水头下降幅度及累计沉降量)都比常渗透系数模型的结果有所减小。

2)在数值模拟实验中，常渗透系数模型和变渗透系数模型的最终沉降差值比与开采量大小和夹层厚度大小均呈正相关；但随着开采量的增加，两模型产生沉降差值的时间逐渐提前，而随着夹层厚度的增大，其时间逐渐滞后。

3)在典型算例中，地下水开采初期，常渗透系数模型和变渗透系数模型计算的沉降量基本一致，若仅对开采初期进行模拟，选用常渗透系数模型即可。从长时间序列的模拟和预测来看，变渗透系数模型更加符合实际沉降过程，随着夹层厚度的增大，忽略垂向渗透系数变化所造成的最终沉降差值也逐渐增大，虽然在较短时间内较大厚度的夹层导致沉降差值不明显，但其会对后期的预测和应用产生较大的影响。

4)本次研究仅对羚羊谷典型算例进行模拟，初步验证了对MODFLOW-SUB模型改进的合理性，为应用到更复杂的实际场地奠定了基础。