渗透化归转化思想,提高数学解题能力
夏仕娴

【摘 要】 近年来,随着教育改革的不断深入,教师越来越注重学生综合素质的提高。化归转化思想作为数学学科中常用的解题思想,也受到越来越广泛的关注。它旨在化繁为简、化未知为已知等,从而帮助学生更加高效地解题。因此,如何在教学中渗透化归转化思想、提高学生的数学解题能力成为众多初中数学教师的研究重点。
【关键词】 初中数学;化归转化思想;解题能力
化归转化思想,即将一个问题由复杂化为简单的过程,它是一种十分高效的数学学习方法。众所周知,数学与生活紧密相连,学习数学的最终目的就是将所学知识应用到实际中解决相关数学问题。但是学生往往学的是理论知识,教师不可能将所学的数学问题都一一讲解。在面对问题时,大家应当分析思考,将其与所学知识相联系,化归转化,进而进行求解。因此,教师应当在教学时渗透化归转化思想,引导学生掌握数学解题的方法,进而提高数学解题能力。下面,我将围绕初中数学中化归转化思想的培养策略展开论述。
一、变形,化陌生为熟悉
题是永远做不完的,数学题目千变万化,但是万变不离其宗,题目背后考查的知识点是固定不变的。在学习数学时,很多学生都会产生畏惧心理,在面对数学问题时,这部分学生总觉得没有学过,不会求解。归根结底是因为大家没有融会贯通。为了解决这一问题,教师应在教学时带领大家掌握数学变形,化陌生为熟悉,学会将数学问题转化为学过的知识,进而求解得出正确答案。
1.条件变形,梳理数量关系
数量关系是数学问题中十分重要的条件。只有弄清楚数量关系后,才能继续探究求解。而在应用化归思想解题时,学生需要将已知条件进行变形梳理,从中得出数量关系,方便后续求解。因此,教师应在教学时向学生讲解条件变形的方法,引导大家形成意识,合理利用已知条件,梳理数量关系。
例如,在讲解“乘法公式”时,教师可以向学生讲解这样一个问题:已知a+b=7,ab=10,求(a-b)2。这道题目最终让求解的是(a-b)2,又因为(a-b)2=a2-2ab+b2,因此,大家就需要从已知条件中寻找a2、ab和b2的值,可是观察已知条件发现并没有说明a2和b2,这个时候很多学生就不知道该怎么办了。可是已知条件a+b=7还没有用,回想完全平方公式(a+b)2=a2+2ab+b2,这时候就可以结合这一公式将已知条件进行转化,得出a2+b2=(a+b)2-2ab,即29,紧接着就可以利用这一条件得出(a-b)2=9。
在面对稍微复杂的数学问题时,学生往往无法直接从已知条件中获取数量关系。这时,大家就需要结合所学知识,对已知条件进行变形,梳理得出有用的数量关系。这一步骤直接影响了大家的解题效率,如果解题方法、角度选择不恰当,就很容易增加解题的难度。
2.问题变形,探究问题实质
练习时,学生常常会遇到这样一种情况:题目往往让学生无从下手,大家无法很快得出考查内容的答案。这时候,教师就可以对结果进行变形,将其转化为与已知条件相关联的形式,寻找问题本质。因此,教师可以在教学时向学生展示讲解,带领大家了解并掌握结论变形的使用情况及方法,从而提高其数学解题效率。
例如,在教学“分式方程”时,教师可以出示这样一道题目:若m- =3,求 的值。看到这道题目,可能很多学生都会直接对分式方程求解,计算得出m的值后,代入所求式子计算最终值。但是分式方程具有一定的难度,計算量大,这时候学生就可以从结论入手,对结论进行变形,分子分母同时除以m2,化简可以得出m2-2+ ,这样就可以看出它是(m- )2的展开式形式,然后得出结果为9,这样相对于解分式方程,计算量小很多。
对问题变形的目的在于探究问题的本质。只有明白其本质考查点,学生才能更加高效地找到解题方法和思路。所以,在面对不熟悉的问题时,大家应分析思考,选择变形方法后,寻求突破口,化陌生为熟悉,提高解题能力。
二、分割,化复杂为简单
面对较为复杂的数学问题,学生往往会无从下手,不知道如何分析求解,但其实质只是对知识点的综合考查。在解决较为复杂的问题时,大家就可以使用分割的方法进行化归,化复杂为简单,进而帮助自己求解。因此,为了帮助大家更好地了解并掌握分割化归的方法,教师可以在课堂上进行讲解,引导学生掌握方法,提高数学解题能力。
1.做辅助线,茅塞顿开
初中数学几何问题中,往往会出现很多不规则图形的相关问题,它们没有特定的解题公式、步骤等。针对这种情况,做辅助线分割就是一种很好的解题方法,它可以将不规则图形分割成不同的规则图形,这时候就可以应用所学知识求解了。因此,教师可以在教学时向学生讲解辅助线分割的方法,引导大家掌握其方法内涵,化复杂为简单,提高解题能力。
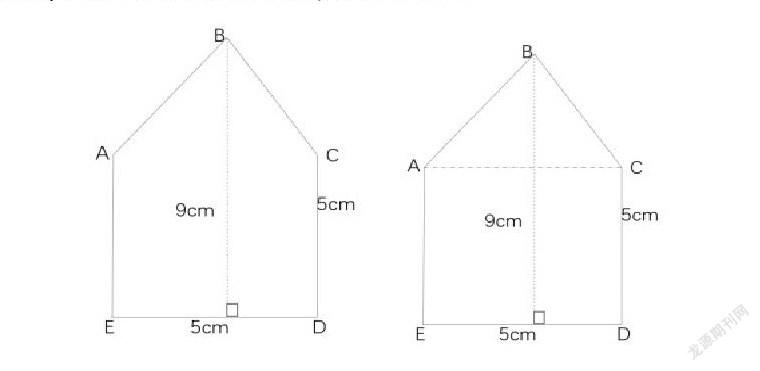
例如,在讲解“三角形”时,可以练习如下的题目:如下左图所示,已知AE⊥ED,CD⊥ED,且AE=CD=ED=5cm,计算图形的面积。这个图形既不是我们所学过的长方形,也不是正方形、三角形等,它无法通过公式直接计算得出答案。这时候,大家就可以在中间构建一条辅助线,如右图所示,这样一来,就可以将其分割成一个三角形和一个正方形。分别计算三角形和正方形的面积为10 cm2和25 cm2。相加即可得出该图形的面积为35 cm2。这样一来,就可以化复杂为简单,将其转化为学过的面积求解问题,分步求解,然后相加得出最终结果。
添助辅助线,将复杂图形分割成几部分,能够启发大家找到解题思路,进而求解得出正确答案。但是值得注意的是,辅助线的画法是灵活的,往往有多种形式,因此,学生在做辅助线时不必拘泥于某种特定形式,只要能帮助化繁为简即可。
2.移动填充,另辟蹊径
分割能够帮助大家将复杂的问题拆分成一个个简单的部分,简化题目难度。但是很多时候,移动填充,将不规则图形通过分割移动转化成等价的规则图形,相对来说计算量更小。
因此,教师可以在教学时引导学生移动填充,另辟蹊径。这样不仅能够提升数学解题能力,还有助于帮助大家融会贯通,发散数学思维,提升数学素养。
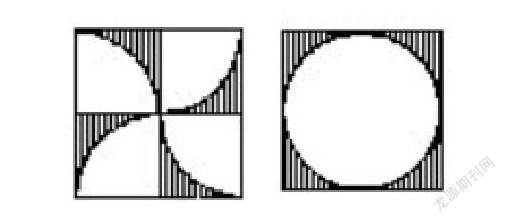
例如,在教学“圆的面积”时,可以讲解如下所示的例题:如下左图所示,已知正方形的边长为10cm,求解阴影部分的面积。观察可以发现阴影部分是不规则图形,直接对阴影部分计算求解可能不太现实,无法计算,因此,这个时候大家就可以思考了,这4个 圆全等,因此,如果将其移动旋转,那么就可以得到如下右图所示的样子,此时的阴影部分与左图部分面积是相等的。所以,大家只需要计算右边所示的阴影部分面积即可。很显然,这部分面积可以用正方形面积-圆的面积计算出来,即结果为(100-25π) cm2。这样一来,就可以通过规则图形求解不规则图形的面积。
移動填充,能够将不规则图形转化为规则图形,大大降低了题目难度。但这种方法却并非十分容易,学生需要在日常学习中不断练习并积累经验。
三、建模,化抽象为具体
数学是一门有规律的学科。在解决数学问题时,学生可以构建数学模型,化抽象为具体。这样,明白了考查点后,学生就可以应用所学知识分析求解。其中,构建模型是十分关键的步骤,模型的构建直接影响最终的学习效果。因此,教师可以在教学过程中带领大家练习,经历过程,促进掌握建模的方法和意义,提高数学学习效率。
1.分析等量,创建方程模型
方程是初中数学中常见的模型。构建方程模型,计算求解,能够计算得出所需要的未知量。构建方程模型的前提就是分析等量关系。因此,教师可以向学生讲解等量关系的分析方法,只有得出了正确的等量关系,才能构建出正确的方程模型。
例如,在教学“一元二次方程”时,教师可以出示这样一道题目:某树林原有树木8行8列,后来又增加了36棵树,且增加的行数和列数相等,请问现在有多少行和列。分析等量关系,之前的树木+36=之后的树木,那么可以构建方程模型,即假设现在有x行和x列树木,那么列方程为8×8+36=x2,计算得出现在有10行和10列树木。可见,构建方程模型能够十分清晰地展现等量关系,大家只需要应用所学知识求解方程即可。但是在构建方程模型求解时,学生需要注意两个方面:一是记清楚未知数x代表哪个量,若不是所求量,那么求解出方程后还要继续计算;二是方程式并不是固定不变的,学生不必纠结,只需要保证方程式的正确性即可。
分析等量、创建方程模型,能够化抽象为具体,提高解题效率。同时,这需要大家熟练了解方程知识,牢固掌握解方程的几种方法。
2.抽取规律,构建函数模型
函数反映了事物之间的联系,应用函数能够帮助大家探究并发现事物之间的规律。因此,在解决一些实际问题时,学生就可以抽取规律,为其构建函数模型。这是一种十分常见且重要的数学模型,具有广泛的应用价值。
例如,在教学“一次函数”时,可以带领学生分析这样一个问题:若某船只在水上航行时,其顺流比逆流每小时多前进4公里,若水流的速度已知,并保持不变,请问该船只顺流时船的速度与船在静水中的速度之间是怎样的大小关系。首先,大家需要分析顺流和逆流,即顺流速度=船在静水中的速度+水速,逆流速度=船在静水中的速度-水速,那么可以发现规律,顺流速度-逆流速度=2水速,因此,结合已知条件就可以计算出水速为2千米/时,紧接着就可以构建函数模型,表示顺流、逆流与船速的关系。即假设船在静水中的速度为x千米/小时,那么顺流时船实际的速度y=x+2,即呈一次函数关系。
可见,构建函数模型,应用函数知识能够帮助学生更好地分析和探究,解决数学问题。但是它并不适用于所有问题,大家还是应当判断思考,选取最佳解题方案,提高解题效率。
总的来说,化归转化思想在数学学习中有着十分重要的应用。但是它的形成并非一蹴而就的,教师应当具有充足的耐心。不断总结改进,着力打造高效数学课堂,将化归思想渗透在日常教学中。通过教学练习,引导学生掌握其思想内涵,提高数学解题能力,为以后的数学学习打下坚实的基础。

